RBSE Solutions for Class 7 Maths Chapter 6 त्रिभुज और उसके गुण Ex 6.4

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 6 त्रिभुज और उसके गुण Ex 6.4 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.4

प्रश्न 1.
निम्न दी गई भुजाओं की मापों से क्या कोई त्रिभुज सम्भव है?
(i) 2 cm, 3 cm, 5 cm
हल:
क्योंकि 2 + 3 4 5 अतः, दी गई भुजाओं की मापों से त्रिभुज सम्भव नहीं

(ii) 3 cm, 6 cm, 7 cm
हल:
3 + 6 > 7, 3 + 7 > 6 और 6 + 7 > 3
अर्थात् किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा है।
अतः, इन मापों से त्रिभुज बनाना सम्भव है।

(iii) 6 cm, 3 cm, 2 cm
हल:
6 + 3 > 2, 3 + 2 ≯ 6
अतः, दी गई भुजाओं की मापों से त्रिभुज सम्भव नहीं

प्रश्न 2.
त्रिभुज PQR के अभ्यन्तर में कोई बिन्दु 0 लीजिए। क्या यह सही है कि

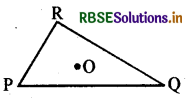
(i) OP + OQ > PQ ?
(ii) OQ + OR > QR ?
(iii) OR + OP > RP ?
हल:
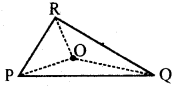
त्रिभुज के गुण द्वारा Δs, OPQ, OQR और OPR में,
(i) OP + OQ > PQ
(ii) XOQ + OR > QR
(iii) OR + OP > RP

प्रश्न 3.
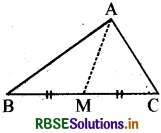
त्रिभुज ABC की एक माध्यिका AM है। बताइए कि क्या
AB + BC + CA > 2AM ?

हल:
त्रिभुज की असमिकाओं का प्रयोग करके ΔABM और ΔAMC में 
AB + BM > AM .... (1)
और CA + MC > AM .... (2) 
(1) और (2) के दोनों पक्षों को जोड़ने पर 
AB + (BM + MC) + CA > AM + AM 
या AB + BC + CA > 2AM

प्रश्न 4.
ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA > AC + BD ? 
हल:
माना ABCD एक चतुर्भुज है। AC और BD को मिलाओ।

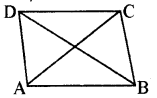
त्रिभुज की असमिकाओं का प्रयोग करके ΔABC, ΔDAC, ΔABD और ΔCBD में,
AB + BC > AC .... (1)
CD + DA > AC ..........(2)
AB + AD > BD ... (3)
और BC + CD > BD .... (4) 

(1), (2), (3) और (4) को दोनों ओर जोड़िए
2(AB + BC + CD + AD) > 2(AC + BD)
या (AB + BC + CD + AD) > (AC + BD) 

प्रश्न 5. 
ABCD एक चतुर्भुज है। क्या AB + ,BC + CD + DA < 2(AC + BD) ?
हल:
माना ABCD एक चतुर्भुज है और AC और BD इसके कर्ण हैं जो 0 पर काटते हैं।

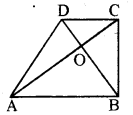
त्रिभुज की असमिकाओं का प्रयोग करके 
ΔOAB में, OA + OB > AB .... (1)
इसी प्रकार, ΔBOC, AΔCOD और ΔAOD से क्रमशः हमें प्राप्त होता है।
OB + OC > BC .... (2)
OC + OD > DC .... (3)
OD + OA > DA .... (4) 

इन चारों परिणामों (1), (2), (3) और (4) को जोड़ने
2(OA + OB + OC + OD) > AB + BC + CD + DA
या 2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA
या 2(AC + BD) > AB + BC + CD + DA
या AB + BC + CD + DA < 2(AC + BD)

प्रश्न 6.
एक त्रिभुज की दो भुजाओं की माप 12 cm तथा 15 cm है। इसकी तीसरी भुजा की माप किन दो मापों के बीच होनी चाहिए?
हल:
माना तीसरी भुजा की लम्बाई x cm है। तो 12 + 15 >x, x + 12 > 15 और x + 15 > 12
या 27 > x, x > 3 और x > - 3
3 और 27 के बीच की संख्याएँ इन्हें सन्तुष्ट करेंगी।
∴ तीसरी भुजा की लम्बाई 3 cm और 27 cm के बीच कोई लम्बाई होगी।