RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.4

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.4 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.4

Question 1.
Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
Answer:
As, we know that in a triangle sum of the lengths of two sides is always greater than the length of the third side. v
2 cm, 3 cm, 5 cm 
We have 2 + 3 = 5
⇒ Sum of the lengths of two sides
= length of the third side 
∴ A triangle cannot be possible with these sides.

(ii) 3 cm, 6 cm, 7 cm
Answer:
3 cm, 6 cm, 7 cm
3 + 6 > 7, 6 + 3 > 7 and 7 + 3 > 6
∴ A triangle can be possible with these three sides.

(iii) 6 cm, 3 cm, 2 cm
Answer:
6 cm, 3 cm, 2 cm'
We see that 6 + 3 > 2, 3 + 2 < 6 and 6 + 2 > 3 
∴ A triangle cannot be possible with these sides.

Question 2. 
Take any point O in the interior of a triangle PQR. Is :

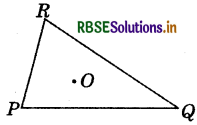
(i) OP + OQ > PQ?
Answer:
Yes OP + OQ> PQ 
∵ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

(ii) OQ + OR > QR?
Answer:
Yes OQ + OR > QR
∵ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

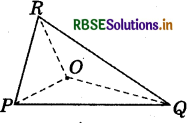
(iii) OR + OP > RP?
Answer:
Yes OR + OP>RP 
∵ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Question 3.
AM is a median of a triangle ABC. Is AB + BC + CA > 2AM?
(Consider the sides of triangles ΔABM and ΔAMC.)

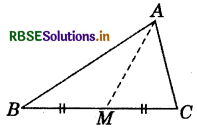
Answer:
In AABM, AB + BM > AM „.(i) v Sum of the lengths of any two sides of a triangle is greater than the length of the third side. 
In AACMyCA + CM>AM ...(ii)
∵ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Adding (i) and (ii),
AB + BM+CA + CM >AM + AM
AB + (BM+CM) + CA > 2AM
AB + BC + CA > 2AM

Question 4.
ABCD is quadrilateral.
Is AB + BC + CD + DA > AC + BD?

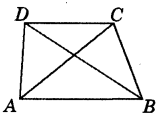
Answer:
In ΔABC, AB + BC > AC ...(i)
∵ Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
In ΔACD, CD + DA > AC ...(ii)

Adding (i) and (ii),
AB + BC + CD + DA > 2AC ...(iii)
In ΔABD, AB + DA > BD ...(iv)
In ΔBCD, BC + CD > BD ...(v)

Adding (iv) and (v),
AB + DA + BC + CD >2BD ...(vi)

Adding (iii) and (vi),
2(AB + BC + CD + DA) > 2(AC + BD) 
AB + BC + CD + DA > AC + BD

Question 5.
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2(AC + BD)?

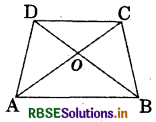
Answer:
In ΔOAB, (OA + OB) >AB ...(i)
In ΔOBC, {OB + OC) > BC ...(ii)
In ΔOCD, {OC + OD) > CD ...(iii)
 
In ΔOAD, {OA + OD)>AD ...(iv)
Adding (i), (ii), (iii) and (iv), 
we have OA + OB + OB + OC + OC + OD + OA + OD > AB + BC + CD + DA 
⇒ AB + BC + CD + DA< 2(OA + OB + OC + OD)
⇒ AB+BC + CD + DA< 2 [{OA + OC) + {OB + OD)]
⇒ AB + BC + CD + DA < 2(AC + BD)

Question 6.
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Answer:
The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Let x cm be the length of third side.
∴ 12 + 15 > x ⇒ 27 > x ⇒ x < 27
15 + x > 12 ⇒ x > 12 - 15 ⇒ x > -3
x + 12 > 15 ⇒ x > 15 - 12 ⇒ x > 3
x > - 3 and x > 3 ⇒ x > 3
∴ Length of third side should be any length between 3 cm and 27 cm.