RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.3

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.3 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.3

Question 1.
Find the value of the unknown x in the following diagrams:

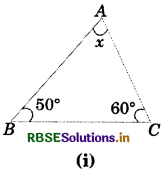
Answer:
Sum of interior angles of a triangle
= 180°
x + 50°+ 60° = 180°
(Angles sum property of a triangle) 
⇒ x + 110° = 180°
⇒ x = 180°-110° = 70°

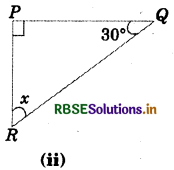
Answer:
x + 90° + 30° = 180°
(Angles sum property of a triangle)
⇒ x + 120° = 180°
⇒ x = 180° - 120° = 60°

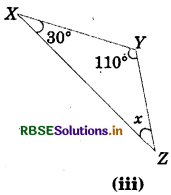
Answer:
x + 30° + 110° = 180°
(Angles sum property of a triangle)
⇒ x + 140° = 180°
⇒ x = 180°-140° =40°

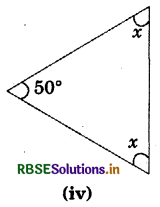
Answer:
x + x + 50° = 180°
(Angles sum property of a triangle)
⇒ 2x = 180° - 50° 
⇒ 2x = 130°
⇒ x = \(\frac{130^{\circ}}{2}\) = 65°

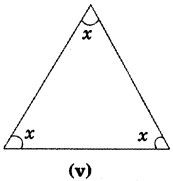
Answer:
x + x + x = 180°
(Angles sum property of a triangle)
⇒ 3x = 180°
⇒ x = \(\frac{180^{\circ}}{3}\) = 60° 

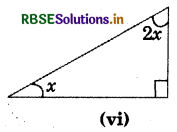
Answer:
x + 2x + 90° =180°
(Angles sum property of a triangle)
⇒ 3x = 180° - 90°
⇒ 3x =90°
⇒ x = \(\frac{90^{\circ}}{3}\) = 30°

Question 2. 
Find the value of the unknown x and y in the following diagrams :

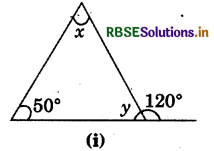
Answer:
Angles y and 120° are linear pair. 120° + y = 180°
⇒ y = 180° -120°
⇒ y = 60°
∵ x + 60° + 50° = 180°
(Angles sum property of a triangle) 
⇒ x = 180°- 110° ⇒ x = 70°
Thus, x = 70°, y = 60°

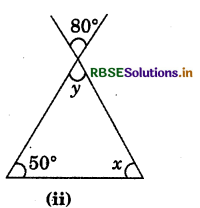
Answer:
Since vertically opposite angles are equal.
∴ y = 80°
Using angles, sum property of a triangle, 
50° + 80° + x = 180°
⇒ x = 180° - 130° = 50°
∴ x = 50°

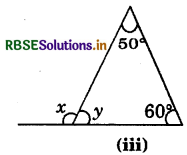
Answer:
Using angles, sum property of a triangle,
50° + 60° + y = 180°
⇒ y = 180°-110° = 70°
Also x and y form a linear pair,
x + y = 180° 
⇒ x + 70° = 180° 
⇒ x = 180°-70° = 110°
⇒ x = 110°

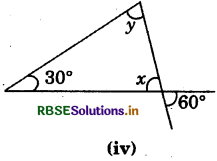
Answer:
Since vertically opposite angles are equal.
∴ x = 60°
Using angles sum property of a triangle,
x + y + 30° = 180°
⇒ 60° + y + 30° = 180°
⇒ y = 180° - 90° 
⇒ y = 90°

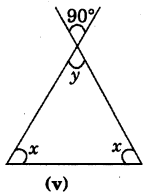
Answer:
Since vertically opposite angles are equal.
∴ y = 90° 
Using angles sum property of a triangle.
x + x + y = 180°
⇒ 2x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ 2x = 90° ⇒ x = \(\frac{90^{\circ}}{2}\) ⇒ x = 45°

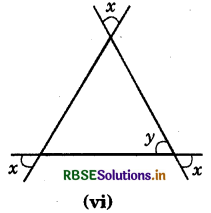
Answer:
Since vertically opposite angles are equal.
∴ x = y
and other vertically opposite angles are x.
Now, using angles sum property of a triangle,
x + x + x = 180° 
⇒ 3x = 180°
⇒ x = \(\frac{180^{\circ}}{3}\)
⇒ x = 60°
∴ y = 60° [∴x = y]