RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 5 रेखा एवं कोण Intext Questions

(सोचिए, चर्चा कीजिए एवं लिखिए पृष्ठ 107)

प्रश्न 1.
क्या दो न्यून कोण एक-दूसरे के पूरक हो सकते हैं?
हल:
हाँ, दो न्यून कोण एक-दूसरे के पूरक हो सकते हैं यदि उनका योग 90° हो।

प्रश्न 2.
क्या दो अधिक कोण एक-दूसरे के पूरक हो सकते हैं?
हल:
नहीं, दो अधिक कोण एक-दूसरे के पूरक नहीं हो सकते; क्योंकि उनका योग 90° नहीं होता है।

प्रश्न 3.
क्या दो समकोण एक-दूसरे के पूरक हो सकते हैं?
हल:
नहीं, दो समकोण एक-दूसरे के पूरक नहीं हो सकते; क्योंकि उनका योग 180° होता है।

(प्रयास कीजिए पृष्ठ 107)

प्रश्न 1.
निम्नलिखित कोणों के युग्मों में कौनसे पूरक हैं?

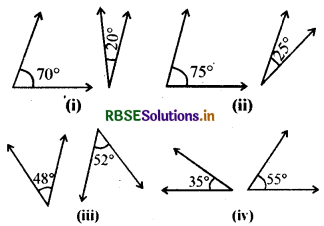
हल:
(i) दो कोणों का योग = 70° + 20° = 90°
अतः, कोणों का यह युग्म पूरक होगा।

(ii) दो कोणों का योग = 75° + 25° = 100° ≠ 90°
अतः, कोणों का यह युग्म पूरक नहीं होगा।

(iii) दो कोणों का योग = 48° +52° = 100° ≠ 90°
अतः, कोणों का यह युग्म पूरक नहीं होगा।

(iv) दो कोणों का योग = 35° + 55° = 90°
अतः, कोणों का यह युग्म पूरक होगा।

प्रश्न 2.
निम्नलिखित कोणों में प्रत्येक के पूरक का से माप क्या है?
(i) 45°
(ii) 65°
(iii) 41°
(iv) 54°
हल:
हम जानते हैं कि किसी कोण और इसके पूरक कोण का योग 90° होता है। अतः
(i) 45° के कोण के पूरक कोण का माप
= (90° - 45°) = 450

(ii) 65° के कोण के पूरक कोण का माप
= (90° - 65°) = 25°

(iii) 41° के कोण के पूरक कोण का माप
= (90° - 41°) = 49°

(iv) 54° के कोण के पूरक कोण का माप
= (90° - 54°) = 36°

प्रश्न 3.
दो पूरक कोणों के मापों का अन्तर 12° है। कोणों के माप ज्ञात कीजिए।
हल:
माना एक कोण x° है तो दूसरा कोण (x + 12)° होगा। अब x° और (x + 12)° पूरक कोण होंगे।
∴ x + (x + 12) = 90°
या 2x + 12 = 90°
या 2x = 90 - 12
या 2x = 78
या x = \(\frac{78}{2}\) = 39
अतः दो कोणों की माप 39° और 39° + 12° = 51° होगी।

(सोचिए, चर्चा कीजिए एवं लिखिए। पृष्ठ 108)

प्रश्न 1.
क्या दो अधिक कोण सम्पूरक हो सकते हैं?
हल:
नहीं, दो अधिक कोण सम्पूरक नहीं हो सकते

प्रश्न 2.
क्या दो न्यून कोण सम्पूरक हो सकते हैं?
हल:
नहीं, दो न्यून कोण सम्पूरक नहीं हो सकते; क्योंकि इन दोनों कोणों का योग 180° नहीं हो सकता।

प्रश्न 3.
क्या दो समकोण सम्पूरक हो सकते हैं? |
हल:
हाँ, दो समकोण हमेशा सम्पूरक होते हैं।

(प्रयास कीजिए पृष्ठ 108)

प्रश्न 1.
आकृति में सम्पूरक कोणों के युग्म ज्ञात कीजिए

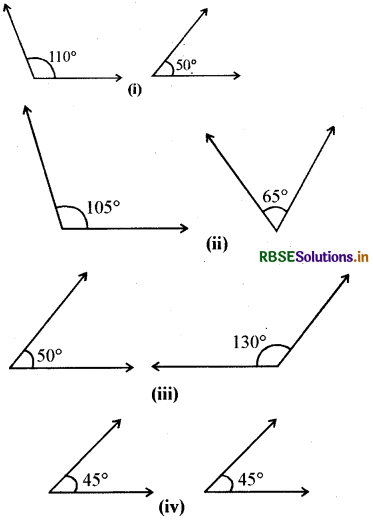
हल:
आकृति (i) में,
कोणों का योग = 110° + 50° = 160° ≠ 180°
अतः, ये सम्पूरक नहीं हैं।
आकृति (ii) में, कोणों का योग = 105° + 65° = 170° ≠ 180°
अतः, ये सम्पूरक नहीं हैं।
आकृति (iii) में,
कोणों का योग = 130° + 50° = 180°
अतः, ये सम्पूरक हैं।
आकृति (iv) में,
कोणों का योग = 45° + 45° = 90° ≠ 180°
अतः, ये सम्पूरक नहीं हैं।

प्रश्न 2.
निम्नलिखित कोणों में प्रत्येक के सम्परक का माप क्या होगा?
(i) 100°
(ii) 90°
(iii) 55°
(iv) 125°
हल:
हम जानते हैं कि एक कोण और इसके सम्पूरक कोण का योग 180° होता है। अतः
(i) 100° के कोण का सम्पूरक कोण (180° - 100°), अर्थात् 80°
(ii) 90° के कोण का सम्पूरक कोण (180° - 90°), अर्थात् 90°
(iii) 55° के कोण का सम्पूरक कोण (180° – 55°), अर्थात् 125°
(iv) 125° के कोण का सम्पूरक कोण (180° - 125°), अर्थात् 55°

प्रश्न 3.
दो सम्पूरक कोणों में बड़े कोण का माप छोटे कोण के माप से 440 अधिक है। कोणों के माप ज्ञात कीजिए।
हल:
माना छोटा कोण x° तो बड़ा कोण (x + 44)°
अब x° और (x + 44)° सम्पूरक कोण होंगे
∴ x + (x + 44) = 180
या 2x + 44 = 180
या 2x = 180 - 44
या 2x = 136
या x = \(\frac{136}{2}\) = 68
अतः, दो कोणों की माप 68° तथा (68° + 44°) = 112° होगी।

(प्रयास कीजिए पृष्ठ 110)

प्रश्न 1.
क्या 1 और 2 से अंकित कोण आसन्न हैं? यदि ये आसन्न नहीं हैं तो बताइए क्यों?

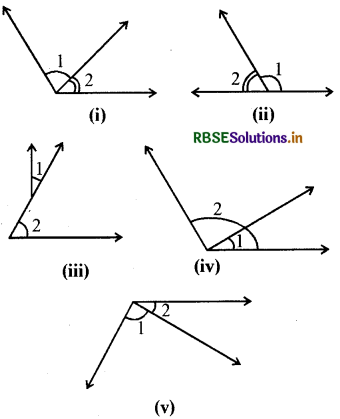
हल:
(i) हाँ, 1 और 2 से अंकित कोण आसन्न हैं।
(ii) हाँ, 1 और 2 से अंकित कोण आसन्न हैं।
(iii) नहीं, 1 और 2 से अंकित कोण आसन्न नहीं हैं; क्योंकि इनमें उभयनिष्ठ शीर्ष नहीं है।
(iv) नहीं, क्योंकि 1 और 2 से अंकित कोणों की अन्य भुजा उभयनिष्ठ भुजा के विपरीत नहीं है।
(v) हाँ, 1 और 2 से अंकित कोण आसन्न हैं।

प्रश्न 2.
आकृति में, क्या निम्नलिखित कोण आसन्न

(a) ∠AOB और ∠BOC
(b) ∠BOD और ∠BOC अपने उत्तर की पुष्टि कीजिए।
हल:
(a) आकृति में, ∠AOB और ∠BOC उभयनिष्ठ शीर्ष तथा उभयनिष्ठ भुजा हैं। इनकी अन्य भुजा उभयनिष्ठ भुजा के विपरीत है। अतः, ∠AOB और ∠BOC आसन्न कोण हैं।
(b) ∠BOD और ∠BOC आसन्न कोण नहीं हैं क्योंकि इनकी अन्य भुजाएँ उभयनिष्ठ OB के विपरीत नहीं हैं।

(सोचिए, चर्चा कीजिए एवं लिखिए पृष्ठ 110)

प्रश्न 1.
क्या दो आसन्न कोण सम्पूरक हो सकते .
हल:
हाँ, दो आसन्न कोण सम्पूरक हो सकते हैं।

प्रश्न 2.
क्या दो आसन्न कोण पूरक हो सकते हैं?
हल:
हाँ, दो आसन्न कोण पूरक हो सकते हैं।

प्रश्न 3.
क्या दो अधिक कोण आसन्न कोण हो | सकते हैं?
हल:
हाँ, दो अधिक कोण आसन्न कोण हो सकते

प्रश्न 4.
क्या एक न्यून कोण, अधिक कोण का | आसन्न हो सकता है?
हल:
हाँ, एक न्यून कोण, अधिक कोण का आसन्न हो सकता है।

(सोचिए, चर्चा कीजिए एवं लिखिए पृष्ठ 111)

प्रश्न 1.
क्या दो न्यून कोण एक रैखिक युग्म बना | सकते हैं?
हल:
नहीं, दो न्यून कोण रैखिक युग्म नहीं बना सकते; क्योंकि रैखिक युग्म में कोणों का योग 180° होता है और दो न्यून कोणों का योग 180° से कम होता है।

प्रश्न 2.
क्या दो अधिक कोण एक रैखिक युग्म बना सकते हैं?
हल:
नहीं, दो अधिक कोण रैखिक युग्म नहीं बना सकते; क्योंकि रैखिक युग्म में दो कोणों का योग 180° होता है और दो अधिक कोणों का योग 180° से अधिक होता है।

प्रश्न 3.
क्या दो समकोण एक रैखिक युग्म बना सकते हैं?
हल:
हाँ, दो समकोण एक रैखिक युग्म बना सकते हैं, यदि उनमें एक उभयनिष्ठ भुजा हो।

(प्रयास कीजिए पृष्ठ 111)

प्रश्न 1.
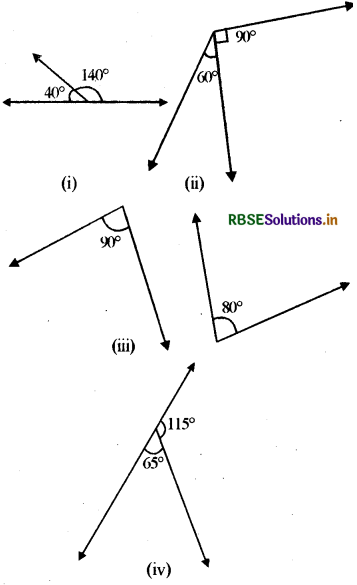
बताइए कोणों के निम्नलिखित युग्मों में से कौनसा रैखिक युग्म बनाता है?

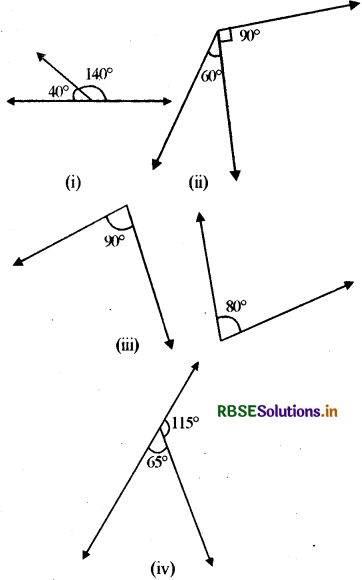
हल:
आकृति (i) में,
कोणों का योग = 140° + 40° = 180°
अतः, जब प्रत्येक को दूसरे के आसन्न रखा जाए, तब यह युग्म रैखिक युग्म बनाता है।
आकृति (ii) में,
कोणों का योग = 60° + 90° = 150° ≠ 180°
अतः, यह युग्म रैखिक युग्म नहीं बना सकता है।
आकृति (iii) में, कोणों का योग = 90° + 80° = 170° ≠ 180°
अतः, यह युग्म रैखिक युग्म नहीं बना सकता है।
आकृति (iv) में, कोणों का योग = 65° + 1150 = 180°
अतः, जब प्रत्येक को दूसरे के आसन्न रखा जाए, तब यह युग्म रैखिक युग्म बनाता है।

(प्रयास कीजिए पृष्ठ 113)

प्रश्न 1.
दी हुई आकृति में, यदि ∠1 = 30°, तो ∠2 एवं ∠3 ज्ञात कीजिए।

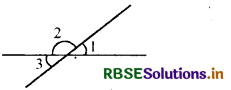
हल:
क्योंकि रेखाएँ एक बिन्दु पर काटती हैं अतः
∠1 = ∠3
[ऊर्ध्वाधर सम्मुख कोण]
या ∠3 = 30°
[∵ ∠1 = 30°, दिया है]
स्पष्टतः, ∠1 + ∠2 = 180°
[∵ ∠1 और ∠2 रैखिक युग्म के कोण हैं]
या 30° + ∠2 = 180°
या ∠2 = 180° - 30°
या ∠2 = 150°
अतः, ∠2 = 150° और ∠3 = 30°

प्रश्न 2.
अपने आसपास से शीर्षाभिमुख कोण का एक उदाहरण दीजिए।

हल:
आकृति में दिखाई गई ग्रिल में शीर्षाभिमुख कोण दर्शाते हैं।

(सोचिए, चर्चा कीजिए एवं लिखिए पृष्ठ 116)

प्रश्न 1.
आकृति में, AC और BE, P पर प्रतिच्छेद करती हैं। AC और BC, C पर प्रतिच्छेद करती हैं।
AC और EC, C पर प्रतिच्छेद करती हैं। प्रतिच्छेदी रेखाखण्डों के दस अन्य युग्म ज्ञात करने का प्रयास कीजिए। क्या दो रेखाएँ अथवा रेखाखण्ड आवश्यक रूप से प्रतिच्छेद करने चाहिए?
क्या आप इस आकृति में दो रेखाखण्डों के युग्म ज्ञात कर सकते हैं जो प्रतिच्छेदी नहीं हैं? क्या दो रेखाएँ एक से ज्यादा बिन्दुओं पर प्रतिच्छेद 1 कर सकती हैं? इसके बारे में विचार कीजिए।

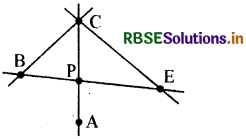
हल:

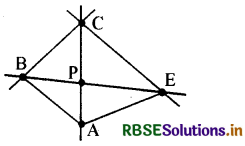
AB और AE को मिलाइए। प्रतिच्छेदी रेखाखण्डों के अन्य दस युग्म हैं-
AP, BP; AP, PE: PB, BC; BC, PC; PC, PE; PE, EC; AB, BC; AB, BP; AE, EC और AE. EP.
कोई दो रेखाएँ अथवा रेखाखण्ड आवश्यक रूप से प्रतिच्छेद नहीं करती हैं।
आकृति में आपस में न काटने वाली रेखाओं के दो युग्म AB और EC, AE और BC.
नहीं, दो रेखाएँ एक बिन्दु से अधिक बिन्दुओं पर प्रतिच्छेद नहीं करतीं।

(प्रयास कीजिए पृष्ठ 116)

प्रश्न 1.
अपने आसपास के परिवेश से ऐसे उदाहरण ज्ञात कीजिए जहाँ रेखाएँ समकोण पर प्रतिच्छेद करती हैं।
हल:
हमारे आसपास के परिवेश में समकोण पर प्रतिच्छेद करने वाली रेखाओं के उदाहरण हैं
(i) ब्लैक बोर्ड के किनारे
(ii) पेपर शीट के किनारे
(iii) मेज की टाँगें और ऊपर का तख्ता
(iv) दीवार पर टंगे कैलेण्डर के किनारे।

प्रश्न 2.
एक समबाहु त्रिभुज के शीर्षों पर प्रतिच्छेदी रेखाओं द्वारा निर्मित कोणों के माप ज्ञात कीजिए।
हल:
माना ABC एक समबाहु त्रिभुज है। हमें इसके कोण ज्ञात करने हैं।
∠A, ∠B तथा ∠C को मापने पर हम पाते हैं-
∠A = ∠B = ∠C = 60°
अथवा
समबाहु त्रिभुज के सभी कोण समान होते हैं, इसलिए

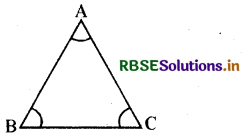
∠A = ∠B = ∠C = x (माना)
∠A + ∠B + ∠C = 180°
या x + x + x = 180°
या 3x = 180°
या x = 60°
∴ ∠A = ∠B = ∠C = 60°

प्रश्न 3.
एक आयत खींचिए और प्रतिच्छेदी रेखाओं द्वारा निर्मित चार शीर्षों के कोणों के माप ज्ञात कीजिए।
हल:
माना ABCD एक आयत है। हमें इसके कोण ज्ञात करने हैं अर्थात् ABCD एक समान्तर चतुर्भुज है जिसमें ∠A = 90°
मापने पर, हम ∠A = ∠B = ∠C = ∠D = 90° पाते हैं।

प्रश्न 4.
यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करती हैं, तो क्या वे हमेशा एक-दूसरे को समकोण पर प्रतिच्छेद करती है?
हल:
नहीं, दो प्रतिच्छेदी रेखाएँ हमेशा समकोण पर प्रतिच्छेद नहीं करतीं।

(प्रयास कीजिए पृष्ठ 117)

प्रश्न 1.
मान लीजिए दो रेखाएँ दी हुई हैं। इन रेखाओं के लिए आप कितनी तिर्यक छेदी रेखाएँ खींच सकते हैं?
हल:
दो दी गई रेखाओं के लिए असंख्य तिर्यक रेखाएँ खींच सकते हैं।

प्रश्न 2.
यदि एक रेखा तीन रेखाओं की तिर्यक छेदी रेखा है, तो बताइए कितने प्रतिच्छेदन बिन्दु हैं?
हल:
अगर तीन रेखाओं की एक तिर्यक छेदी रेखा है | तो इनके तीन या अधिक प्रतिच्छेदन बिन्दु हो सकते हैं।

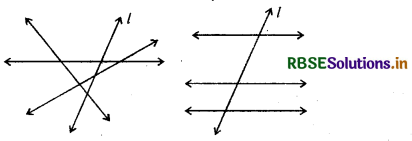
परन्तु, तिर्यक छेदी रेखा तीन रेखाओं को केवल तीन भिन्न बिन्दुओं पर ही काटेगी।

प्रश्न 3.
अपने आसपास कुछ तिर्यक छेदी रेखाएँ ढूँढ़ने का प्रयास कीजिए। ..
हल:
हमारे आसपास Dतिर्यक छेदी रेखाओं के उदाहरण हैं-सकरपारा जाली, खिड़की की ग्रिल, लोहे की A सीढ़ी आदि।

(प्रयास कीजिए पृष्ठ 118)

प्रश्न 1.
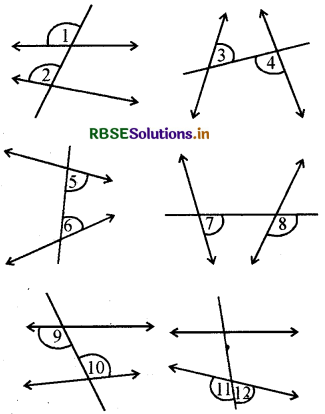
प्रत्येक आकृति में कोण-युग्म को नाम दीजिए:

हल:
प्रथम आकृति में-∠1 और ∠2 संगत कोण
दूसरी आकृति में-∠3 और ∠4 एकान्तर कोण हैं।
तीसरी आकृति में ∠5 और ∠6 तिर्यक छेदी रेखा के एक ही ओर के अन्त:कोण हैं।
चौथी आकृति में-∠7 और ∠8 संगत कोण हैं।
पाँचवीं आकृति में-∠9 और ∠10 एकान्तर कोण
छठी आकृति में-∠11 और ∠12 रैखिक युग्म हैं।

(प्रयास कीजिए पृष्ठ 121)

प्रश्न 1.

(i)

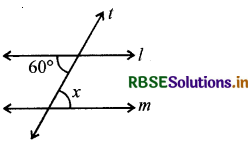
l || m
t एक तिर्यक छेदी रेखा है
∠x = ?
हल:
क्योंकि l || m और t तिर्यक छेदी रेखा है,
इसलिए, ∠x = 60° (एकान्तर कोण)

(ii)

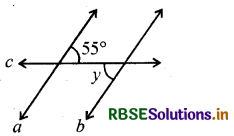
a || b
c एक तिर्यक छेदी रेखा है
∠y = ?
हल:
क्योंकि a || b और c एक तिर्यक छेदी रेखा है,
इसलिए, ∠y = 55° (एकान्तर कोण)

(iii)

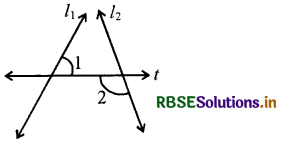
l₁, l₂ दो रेखाएँ हैं
t एक तिर्यक छेदी रेखा है
क्या ∠1 = ∠2 है?
हल:
क्योंकि l₁, और l₂, दो असमान्तर रेखाएँ हैं और t तिर्यक छेदी रेखा है, इसलिए, ∠1 ≠ ∠2
(क्योंकि l₁ || l₂)

(iv)

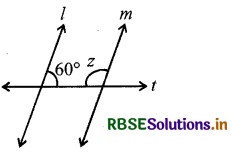
l || m
t एक तिर्यक छेदी रेखा है
∠z = ?
हल:
क्योंकि l || m और t एक तिर्यक छेदी रेखा है,
इसलिए, 60° + z = 180°
(तिर्यक छेदी रेखा के एक ही ओर के अन्त:कोणों का योग 180° होता है।)
या z = 180° - 60° = 120°

(v)

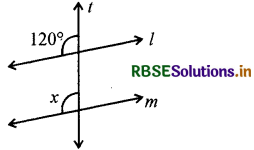
l || m,
t एक तिर्यक छेदी रेखा है
∠x = ?
हल:
क्योंकि l || m और t एक तिर्यक छेदी रेखा है,
इसलिए, ∠x = 120° (संगत कोण)

(vi)

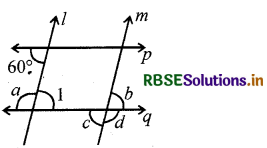
l || m, p || q
a, b, c, d
ज्ञात कीजिए।
हल:
क्योंकि p || q और 1 तिर्यक छेदी रेखा है.
इसलिए, a + 60° = 180°
(तिर्यक रेखा के एक ही ओर के अन्त:कोणों का योग 180° होता है।)
या a = 180° - 60° = 120°
अब, जैसा आकृति में दिखाया गया है, ∠1 चिह्नित करें
तब, ∠1 = 60° (एकान्तर कोण)
क्योंकि l || m और q एक तिर्यक छेदी रेखा है,
इसलिए,
∠c = ∠1 (एकान्तर कोण)
या ∠c = 60° (∵ ∠1 = 60°)
∠b = ∠c (शीर्षाभिमुख कोण)
= 60° (∵ ∠c = 60°)
∠d = 180° - ∠b
= 180° - 60° = 120°
अतः, ∠a = 120°, ∠b = 60°, ∠c = 60°
और ∠d = 120°

(प्रयास कीजिए पृष्ठ 122)

प्रश्न 1.
(i)

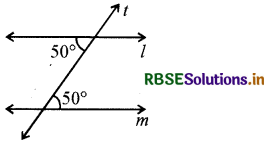
क्या l || m है? क्यों?
हल:
चूँकि एकान्तर कोण बराबर हैं। अतः l || m

(ii)

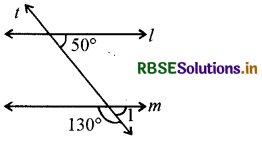
क्या l || m है? क्यों?
हल:
जैसा कि आकृति में दिखाया गया है, ∠1 चिह्नित कीजिए।
∠1 = 180° - 130° = 50°
∴ हम देखते हैं कि संगत कोण समान हैं। अतः l || m.

(iii)

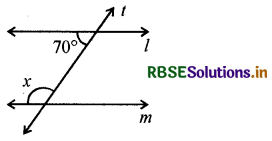
यदि l || m, तो x क्या है?
हल:
क्योंकि l || m और तिर्यक छेदी रेखा है, इसलिए
x + 70° = 180°
(तिर्यक रेखा के एक ही ओर के अन्त:कोणों का योग 180° होता है।)
या x = 180° – 70° = 110°