RBSE Solutions for Class 7 Maths Chapter 5 Lines and Angles Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 5 Lines and Angles Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 5 Lines and Angles Intext Questions

(Think, Discuss and Write: Page No: 95)

Question 1.
Can two acute angles be com¬plement to each other?
Answer:
Yes, because sum of measures of two acute angles can be 90°.

Question 2.
Can two obtuse angles be complement to each other?
Answer:
No, because sum of measures of two obtuse angles cannot be 90° as each obtuse angle is greater than 90°.

Question 3.
Can two right angles be complement to each other?
Answer:
No, because sum of measures of two right angles will be 180°.

(Try These Page No: 95)

Question 1.
Which pair of following angles are complementary?
(i)

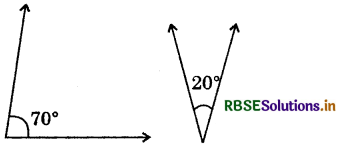
Answer:
∵ 70° + 20° = 90°
∴ Pair of 70°, 20° is the pair of complementary angles.

(ii)

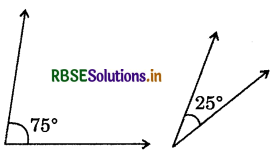
Answer:
∵ 75° + 25° = 100°
∴ Pair of 75°, 25° is not the pair of complementary angles.

(iii)

Answer:
∵ 48° + 52° = 100°
∴ Pair of 48°, 52° is not the pair of complementary angles.

(iv)

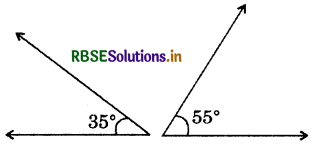
Answer:
∵ 35° + 55° = 90°
∴ Pair of 35°, 55° is the pair of complementary angles.

Question 2.
What is the measure of the com-plement of each of the following angles?
(i) 45°
Answer:
Complementary angle of 45°
= 90° - 45° = 45°

(ii) 65°
Answer:
Complementary angle of 65°
= 90°- 65° = 25°

(iii) 41°
Answer:
Complementary angle of 41°
= 90°- 41° = 49°

(iv) 54°
Answer:
Complementary angle of 54°
= 90° - 54° = 36°

Question 3.
The difference in the measures of two complementary angles is 12°. Find the measures of the angles.
Answer:
Let the smaller angle be x.
∵ Their difference = 12°
∴ The other angle = x + 12°
Since, the sum of the measures of two complementary angles is 90°.
Therefore, x + 12° + x = 90°
⇒ 2x + 12° = 90°
⇒ 2x = 90° - 12°
⇒ 2x = 78°
⇒ x = \(\frac{78^{\circ}}{2}\)
⇒ x = 39°
∴ Smaller angle = 39°
Other angle = 39° + 12° = 51°

(Think, Discuss and Write: Page No: 96)

Question 1.
Can two obtuse angles be supplementary?
Answer:
No, because sum of measure of two obtuse angles will be more than 180°.

Question 2.
Can two acute angles be supplementary?
Answer:
No, because sum of measure of two acute angles will be less than 180°.

Question 3.
Can two right angles be supplementary?
Answer:
Yes, because sum of measure of two right angles will be 180°.

(Try These Page No:96 - 97)

Question 1.
Find the pairs of supplementary angles in:

(i)

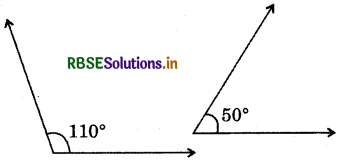
Answer:
∵ 110° + 50° = 160°
∴ Pair of 110° and 50° is not the pair of supplementary angles.

(ii)

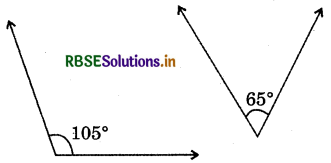
Answer:
∵ 105° + 65° = 170°
∴ Pair of. 105° and 65° is not the pair of supplementary angles.

(iii)

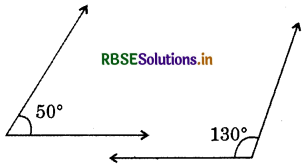
Answer:
∵ 50° + 130° = 180°
∴ Pair of 50° and 130° is the pair of supplementary angles.

(iv)

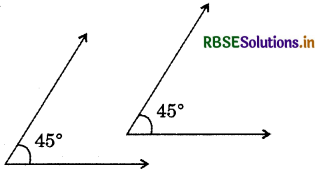
Answer:
∵ 45° + 45° = 90°
∴ Pair of 45° and 45° is not the pair of supplementary angles.

Question 2.
What will be the measure of the supplement of each one of the following angles?
(i) 100°
Answer:
Supplement of 100° = 180° - 100° = 80°

(ii) 90°
Answer:
Supplement of 90° = 180° - 90° = 90°

(iii) 55°
Answer:
Supplement of 55° = 180° - 55° = 125°

(iv) 125°
Answer:
Supplement angle of 125° = 180° - 125° = 55°

Question 3.
Among two supplementary angles the measure of the larger angle is 44° more than the measure of the smaller. Find their measures.
Answer:
Let the smaller angle be x.
Then, measure of larger angle = x + 44°.
Since, the sum of the measures of two supplementary angles is 180°.
Therefore, x + 44° + x = 180°
⇒ 2x + 44° = 180°
⇒ 2x = 180° - 44°
⇒ 2x = 136°
⇒ x = \(\frac{136^{\circ}}{2}\)
⇒ x = 68°
∴ Smaller angle = 68°
Other angle = 68° + 44° = 112°

(Try These Page No: 97 - 98)

Question 1.
Are the angles marked 1 and 2 adjacent? If they are not adjacent, say, 'why'?
(i)

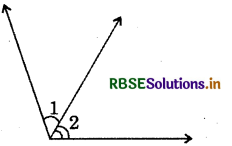
Answer:
Yes, ∠1 and ∠2 are adjacent angles.

(ii)

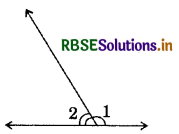
Answer:
Yes, ∠1 and ∠2 are adjacent angles.

(iii)

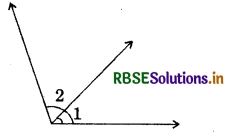
Answer:
No, ∠1 and ∠2 are not adjacent angles because they have no common vertex.

(iv)

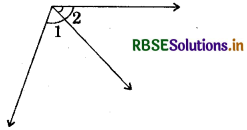
Answer:
No, ∠1 and ∠2 are not adjacent angles because their non-common arms are not on either side of the common arm.

(v)

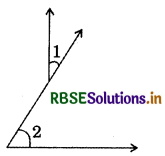
Answer:
Yes, ∠1 and ∠2 are adjacent angles.

Question 2.
In the given figure, are the following adjacent angles.
(a) ∠AOB and ∠BOC
(b) ∠BOD and ∠BOC
Justify your answer.

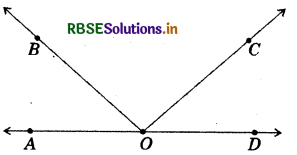
Answer:
(a) Yes, ∠AOB and ∠BOC are.adjacent angles because they have common vertex O, a common arm OB and non-common arms OA and OC are on either side of common arm OB.
(b) No, because there non-common arms OC and OD are not on either side of common arm BO.

(Think, Discuss and Write: Page No: 98)

Question 1.
Can two adjacent angles be supplementary?
Answer:
Yes, two adjacent angles may be supplementary.

Question 2.
Can two adjacent angles be complementary?
Answer:
Yes, two adjacent angles may be complementary.

Question 3. Can two obtuse angles be adjacent angles?
Answer:
Yes, two obtuse angles may be adjacent angles.

Question 4.
Can an acute angle be adjacent to an obtuse angle?
Answer:
Yes, an acute angle and an obtuse angle may be adjacent angles.

(Think, Discuss and Write: Page No: 99)

Question 1.
Can two acute angles form a linear pair?
Answer:
No, because the measure of each acute angle is less than 90° so the sum of the measures of two acute angles is less than 180°.

Question 2.
Can two obtuse angles form a linear pair?
Answer:
No, because the measure of each obtuse angle is more than 90° so the sum of the measures of two obtuse angles is greater than 180°.

Question 3.
Can two right angles form a linear pair?
Answer:
Yes, because the sum of the measures of two right angles is 180°.

(Try These: Page No: 99)

Question 1.
Check, which of the following pairs of angles form a linear pair?
(i)

Answer:
As the sum of linear pair of angles is 180°, then
∵ 140° + 40° = 180°
∴ The pair of angles 140°, 40° form a linear pair.

(ii)

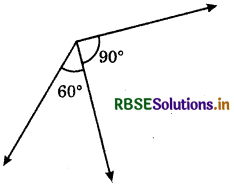
Answer:
As the sum of linear pair of angles is 180°, then
∵ 90° + 60° = 150°
∴ The pair of angles 60°, 60° do not form a linear pair.

(iii)

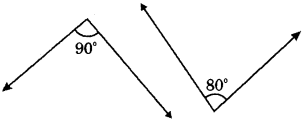
Answer:
As the sum of linear pair of angles is 180°, then
∵ 90° + 80° = 170°
∴ The pair of angles 90° and 80° do not form a linear pair.

(iv)

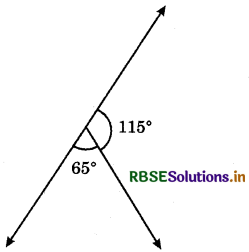
Answer:
As the sum of linear pair of angles is 180°, then
∵ 115° + 65° = 180°
∴ The pair of angles 115°, 65° form a linear pair.

(Try These Page No: 101)

Question 1.
In the given figure, if ∠1 = 30°, find ∠2 and ∠3.

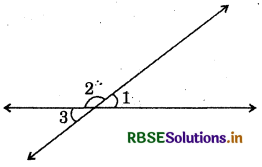
Answer:
∵ ∠3 and ∠1 are vertically opposite angles.
∴ ∠3 = ∠1
∠3 = 30°
Again ∠3 + ∠2 form
∴ ∠3 + ∠2 = 180°
⇒ 30° + ∠2 = 180°
⇒ ∠2 = 180° - 30°
∴ ∠2 = 150°

Question 2.
Give an example for vertically opposite angles in your surroundings.
Answer:
English alphabet ‘X’ is an example of vertically opposite angles.

(Think, Discuss and Write: Page No: 104)

Question 1.
In fig. AC and BE intersect at P.
AC and BC intersect at C, AC and EC intersect at C.
Try to find another ten pairs of intersecting line segments.
Should any two lines or line segments necessarily intersect? Can you find two pair of non-intersecting line segments in the figure?

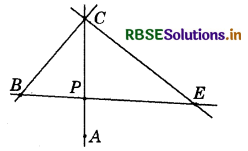
Can two lines intersect in more than one point? Think about it.
Answer:
Various pairs of intersecting lines are:
(a) BC and BE
(b) BP and BC
(c) BC and EC
(d) PC and EC
(e) BE and CE
(f) PE and CE
(g) BP and CP
(i) AP and BP
If any two lines or line segments are not parallel, then they necessarily intersect. In this figure, there is no pair of parallel lines (non-intersecting lines). Two intersecting lines cannot intersect in more than one point, they intersect in one and only one point.

(Try These Page No: 104)

Question 1.
Find examples from your surroundings where lines intersect at right angles.
Answer:
Crossing of the road, English alphabet L, intersection of edges of a cuboid, etc. are the examples where lines intersect at right angles.

Question 2.
Find the measures of the angles made by the intersecting lines at the vertices of an equilateral triangle.
Answer:

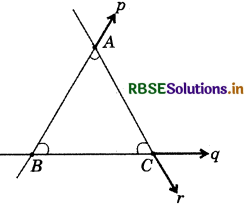
Let lines p, q and r intersects at points A, B and C.
Equilateral triangle so formed is ABC.
Measure of ∠A = 60°
Measure of ∠B = 60°
Measure of ∠C = 60°

Question 3.
Draw any rectangle and find the measures of angles at the four vertices made by the intersecting lines.
Answer:
Let lines p, q, r and s intersects at points A, B, C and D. Rectangle so formed is ABCD.

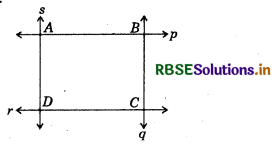
Measure of ∠A = 90°
Measure of ∠B = 90°
Measure of ∠C = 90°
Measure of ∠D = 90°

Question 4.
If two lines intersects, do they always intersect at right angles?
Answer:
No, if two lines intersects, they may or may not be intersects at right angles.

(Try These Page No: 105)

Question 1.
Suppose two lines are given. How many transversals can you draw for these lines?
Answer:
We can draw an infinite number of transversals for two lines.

Question 2.
If a line is a transversal to three lines, how many points of intersections are there?
Answer:
There are three distinct points of intersecting as shown in the figure where line p is the transversal to lines l, m and n.

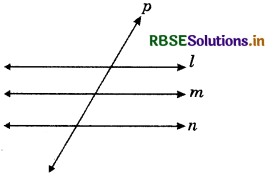
Question 3.
Try to identify a few transversals in your surroundings.
Answer:
(i) A grill of a window.
(ii) A line drawn to intersect the lines of the ruled sheet of paper.

(Try These Page No: 106)

Question 1.
Name the pair of angles in each figures
(a)

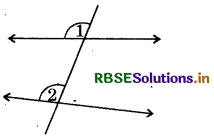
Answer:
∠1 and ∠2 are the pair of corresponding angles.

(b)

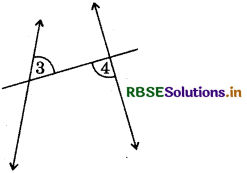
Answer:
∠3 and ∠4 are the pair of alternate interior angles.

(c)

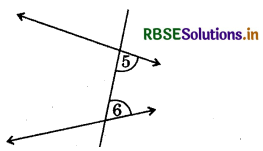
Answer:
∠5 and ∠6 are the pair of interior angles on the same side of the transversal.

(d)

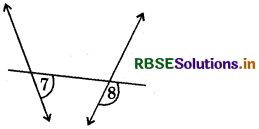
Answer:
(d) ∠7 and ∠8 are the pair of corresponding angles.

(e)

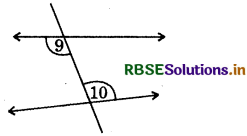
Answer:
∠9 and ∠10 are the pair of alternate interior angles.

(f)

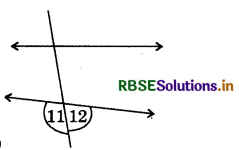
Answer:
∠11 and ∠12 are the linear pair of angles.

(Try These: Page No: 109)

(a)

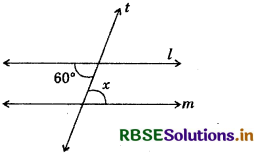
Lines l || m; t is a transversal ∠x = ?
Answer:
Lines l || m, x and 60° are the pair of alternate interior angles, they will be equal, x = 60°
∴ x = 60°

(b)

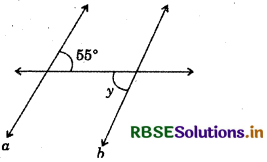
Lines a || b; c is a transversal ∠y = ?
Answer:
Lines a || b, y and 55° are the pair of alternate interior angles, they will be equal.
y = 55°

(c)

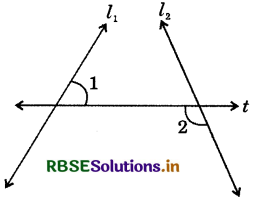
Lines l₁, l₂ be two lines. t is a transversal ∠1 = ∠2 ?
Answer:
(c) ∵ ∠1, ∠2 are the pair of alternate interior angles but lines M and l2 are not parallel.
∴ ∠1 ≠ ∠2

(d)

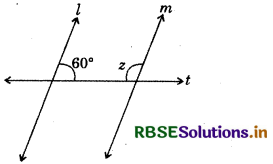
Lines l || m; t is a transversal ∠z = ?
Answer:
Lines l || m, z and 60° are the pair of interior angles on the same side of the transversal, they are supplementary.
∴z + 60° = 180°
⇒ z = 180° - 60°
∴z = 120°

(e)

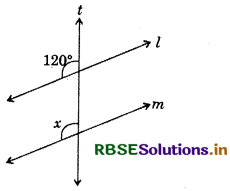
Lines l || m; t is a transversal ∠x = ?
Answer:
Lines l || m and x, 120° are pair of corresponding angles and they are equal.
∴x = 120°

(f)

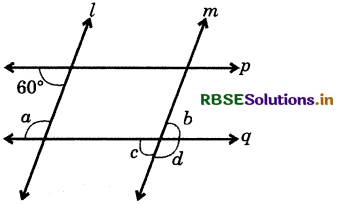
Lines l || m, p || q; find a, b, c, d.
Answer:
∵ Lines p || q, a and 60° are pair of interior angles on the same side of the transversal, they are supplementary.
∴a + 60° = 180°
⇒ a = 180° - 60°
∴a = 120°
∵ Lines M || m and vertically opposite angles of a, and c are the pair of interior angles on the same side of the transversal.
∴a + e = 180°
⇒ 120° + c = 180°
⇒ c = 180° -120° '
∴c = 60°
Now, b and c are vertically opposite angles.
∴ b = 60°
Also, b + d = 180° (linear pair)
⇒ 60° + d = 180°
∴ d = 180° - 60° = 120°

(Try These: Page No: 110)

Question (a)

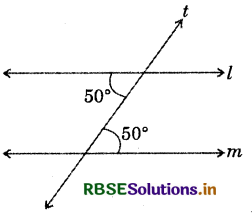
Is l || m? Why?
Answer:
∵ Pair of alternate interior angle is equal.
∴ l || m

Question (b)

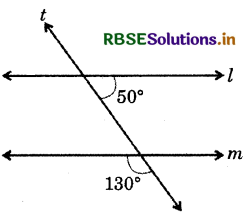
Is l || m? Why?
Answer:
∵ Alternate interior angle of 50° is equal to 180° - 130° = 50°, i.e. alternate interior angles are equal.
∴ l || m

Question (a)

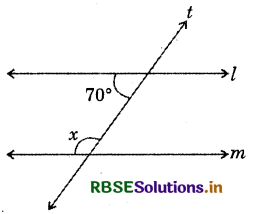
Is l || m? Why ∠x?
Answer:
∵ Lines l || m, x and 70°are the interior angles on the same side of the transversal.
∴ x + 70° = 180°
⇒ x = 180° - 70°
∴ x = 110°