RBSE Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.3

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.3 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 4 Simple Equations Ex 4.3

Question 1.
Solve the following equations:
(a) 2y + \(\frac{5}{2}\) = \(\frac{37}{2}\)
(b) 5t + 28 = 10
(c) \(\frac{a}{5}\) + 3 = 2
(d) \(\frac{q}{4}\) + 7 = 5
(e) \(\frac{5}{2}\)x = - 5
(f) \(\frac{5}{2}\)x = \(\frac{25}{4}\)
(g) 7m + \(\frac{19}{2}\) = 13
(h) 6z + 10 = - 2
(i) \(\frac{3l}{2}\) = \(\frac{2}{3}\)
(j) \(\frac{2b}{3}\) - 5 = 3
Answer:
(a) Given equation is 2y + \(\frac{5}{2}\) = \(\frac{37}{2}\)
Transposing \(\frac{5}{2}\) from L.H.S. to R.H.S.,

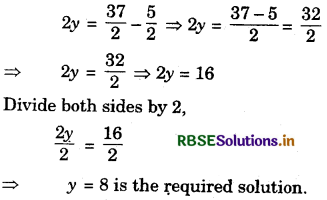
(b) Given equation is 5t + 28 = 10
Transposing 28 from L.H.S. to R.H.S.,
5t = 10 - 28 ⇒ 5t = - 18 Divide both sides by 5,
\(\frac{5 t}{5}=\frac{-18}{5}\)
⇒ t = \(\frac{-18}{5}\) is the required solution.

(c) Given equation is \(\frac{a}{5}\) + 3 = 2
Transposing 3 from L.H.S. to R.H.S.,
\(\frac{a}{5}\) = 2 - 3 ⇒ \(\frac{a}{5}\) = - 1
Multiply both sides by 5,
5 × \(\frac{a}{5}\) = 5 × (- 1)
⇒ a = - 5 is the required solution.

(d) Given equation is \(\frac{q}{4}\) + 7 = 5
Transposing 7 from L.H.S. to R.H.S.,
\(\frac{q}{4}\) = 5 - 7 ⇒ \(\frac{q}{4}\) = - 2
Multiply both sides by 4,
4 × \(\frac{q}{4}\) = (- 2) × 4
⇒ q = - 8 is the required solution.

(e) Given equation is \(\frac{5}{2}\)x = - 5
Multiply both sides by 2,
2 × \(\frac{5}{2}\)x = 2 × (- 5)
⇒ 5x = - 10
Divide both sides by 5,
\(\frac{5 x}{5}=\frac{-10}{5}\)
⇒ x = - 2 is the required solution.

(f)

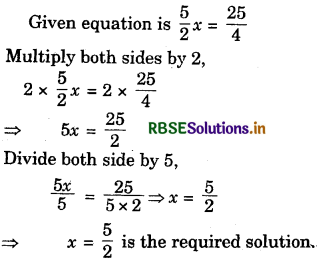
(g) Given equation is 7m + \(\frac{19}{2}\) = 13
Transposing \(\frac{19}{2}\) from L.H.S. to R.H.S.,

(h) Given equation is 6z + 10 = - 2
Transposing 10 from L.H.S. to R.H.S.,
62 = - 2 - 10 ⇒ 6z = - 12
Divide both sides by 6,
\(\frac{6 z}{6}=\frac{-12}{6}\)
⇒ z = - 2 is the required solution.

(i) Given equation is = 3
Multiply both sides by 2,
2 × \(\frac{3 l}{2}\) = 2 × \(\frac{2}{3}\) ⇒ 3l = \(\frac{4}{3}\)
Divide both sides by 3,
\(\frac{3 l}{2}=\frac{4}{3} \times \frac{1}{2}\)
⇒ l = \(\frac{4}{9}\) is the required solution.

(j) Given equation is \(\frac{2 b}{3}\) - 5 = 3
Transposing (- 5) from L.H.S. to R.H.S.,
\(\frac{2 b}{3}\) = 3 + 5 ⇒ \(\frac{2 b}{3}\) = 8
Multiply both sides by 3,
3 × \(\frac{2 b}{3}\) = 3 × 8 ⇒ 2b = 24
Divide both sides by 2,
\(\frac{2 b}{2}=\frac{24}{2}\)
⇒ b = 12 is the required solution.

Question 2.
Solve the following equations:
(a) 2(x + 4) = 12
(b) 3(n - 5) = 21
(c) 3(n - 5) = - 21
(d) - 4(2 + x) = 8
(e) 4(2 - x) = 8
Answer:
(a) Given equation is 2(x + 4) = 12
Divide both sides by 2,
\(\frac{2(x+4)}{2} = \frac{12}{2}\) ⇒ x + 4 = 6
Transpose 4 from L.H.S. to R.H.S.,
x = 6 - 4
⇒ x = 2 is the required solution,

(b) Given equation is 3(n - 5) = 21
Divide both sides by 3,
\(\frac{3(n-5)}{3} = \frac{21}{3}\) ⇒ n - 5 = 7
Transpose - 5 from L.H.S. to R.H.S.,
n = 7 + 5
⇒ n = 12 is the required solution.

(c) Given equation is 3(n - 5) = - 21
Divide both sides by 3,
\(\frac{3(n-5)}{3} = \frac{-21}{3}\) ⇒ n - 5 = - 7
Transpose - 5 from L.H.S. to R.H.S.,
n = - 7 + 5
⇒ n = - 2 is the required solution.

(d) Given equation is - 4(2 + x) = 8
Divide both sides by - 4,
\(\frac{-4(2+x)}{-4} = \frac{8}{-4}\) ⇒ 2 + x = - 2
Transpose 2 from L.H.S. to R.H.S.,
x = - 2 - 2
⇒ x = - 4 is the required solution.

(e) Given equation is 4 (2 - x) = 8
Divide both sides by 4,
\(\frac{4(2-x)}{4} = \frac{8}{4}\) ⇒ 2 - x = 2
Transpose 2 from L.H.S. to R.H.S.,
- x = 2 - 2 ⇒ - x = 0
Multiply both sides by - 1,
(- 1) × (-x) = (- 1) × 0
⇒ x = 0 is the required solution.

Question 3.
Solve the following equations:
(a) 4 = 5(p - 2)
(b) - 4 = 5(p - 2)
(c) 16 = 4 + 3(t + 2)
(d) 4 + 5(p - 1) = 34
(e) 0 - 16 + 4(m - 6)
Answer:
(a) Given equation is 4 = 5(p - 2)
⇒ 5(p - 2) = 4
(An equation remains the same, when the expressions on the left and right are interchanged.)
Divide both sides by 5,
\(\frac{5(p-2)}{5} = \frac{4}{5}\) ⇒ p - 2 = \(\frac{4}{5}\)
Transpose - 2 from L.H.S. to R.H.S.,
p = \(\frac{4}{5}\) + 2 ⇒ p = \(\frac{4+10}{5}\)
⇒ p = \(\frac{14}{5}\) is the required solution.

(b) Given equation is - 4 = 5(p - 2) or 5(p - 2) = - 4
Divide both sides by 5,
\(\frac{5(p-2)}{5}\) = \(\frac{-4}{5}\) ⇒ p - 2 = \(\frac{-4}{5}\)
Transpose - 2 from L.H.S. to R.H.S.,
P = \(\frac{-4}{5}\) + 2 ⇒ P = \(\frac{-4+10}{5}\)
⇒ p = \(\frac{6}{5}\) is the required solution.

(c) Given equation is 16 = 4 + 3(t + 2) or 4 + 3(t + 2) = 16
Transpose 4 from L.H.S. to R.H.S.,
3(t + 2) = 16 - 4 ⇒ 3(t + 2) = 12
Divide both sides by 3,
\(\frac{3(t+2)}{3}\) = \(\frac{12}{3}\) ⇒ t + 2 = 4
Transpose 2 from L.H.S. to R.H.S.,
t = 4 - 2
⇒ t = 2 is the required solution.

(d) Given equation is 4 + 5(p - 1) = 34
Transpose 4 from L.H.S. to R.H.S.,
5(p - 1) = 34 - 4 ⇒ 5(p - 1) = 30
Divide both sides by 5,
\(\frac{5(p-1)}{5}\) = \(\frac{30}{5}\) ⇒ p - 1 = 6
Transpose - 1 from L.H.S. to R.H.S.,
p = 6 + 1
⇒ p = 7 is the required solution.

(e) Given equation is 0 = 16 + 4(m - 6)
⇒ 16 + 4(m - 6) = 0
Transpose 16 from L.H.S. to R.H.S.,
4(m - 6) = 0 - 16 ⇒ 4(m - 6) = - 16
Divide both sides by 4,
\(\frac{4(m-6)}{4}\) = \(\frac{-16}{4}\) ⇒ m - 6 = - 4
Transpose - 6 from L.H.S. to R.H.S.,
m = - 4 + 6
⇒ m = 2 is the required solution.

Question 4.
(a) Construct 3 equations starting with x = 2.
(b) Construct 3 equations starting with x = -2.
Answer:
(a) 1. Let x = 2
Multiply both sides by 5,
5x = 10
Subtract 5 from both sides,
5x - 5 = 10 - 5 ⇒ 5x - 5 = 5

2. Let x = 2
Divide both sides by 3, add 5 to both sides,

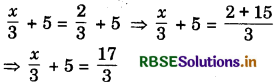
3. Let x = 2
Multiply both sides by 20,
20x = 40
Subtract 20 from both sides,
20x - 20 = 40 - 20 ⇒ 20x - 20 = 20

(b) 1. Let x = - 2
Multiply both sides by 3,
3x = - 6
Subtract 2 from both sides,
3x - 2 = - 6 - 2 ⇒ 3x - 2 = - 8

2. Let x = - 2
Multiply both sides by 5,
5x = - 10
Subtract 1 from both sides,
5x - 1 = - 10 - 1 ⇒ 5x - 1 = - 11

3. Let x = - 2
Divide both sides by 4,
\(\frac{x}{4}=\frac{-2}{4} \Rightarrow \frac{x}{4}=-\frac{1}{2}\)
Add 4 to both sides,
\(\frac{x}{4} + 4 = \frac{-1}{2} + 4 = \frac{-1+8}{2}\)
⇒ \(\frac{x}{4}\) + 4
= \(\frac{7}{2}\) is the required solution.