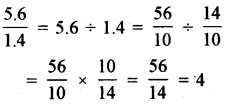RBSE Solutions for Class 7 Maths Chapter 2 भिन्न एवं दशमलव Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 2 भिन्न एवं दशमलव Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 2 भिन्न एवं दशमलव Intext Questions

(प्रयास कीजिए - पृष्ठ 34-1)

प्रश्न 1.
ज्ञात कीजिए :
(a) \(\frac{2}{7}\) × 3
(b) \(\frac{9}{7}\) × 6
(c) 3 × \(\frac{1}{8}\)
(d) \(\frac{13}{11}\) × 6
यदि गुणनफल एक विषम भिन्न है तो इसे मिश्रित भिन्न के रूप में व्यक्त कीजिए।
हल:

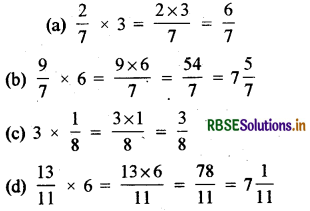
प्रश्न 2.
2 × \(\frac{2}{5}\) = \(\frac{4}{5}\) को सचित्र निरूपित कीजिए।
हल:
2 × \(\frac{2}{5}\) = \(\frac{4}{5}\) को निम्न तरीके से प्रकट कर सकते हैं:

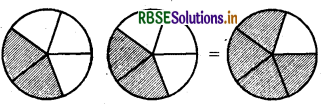
इस प्रकर 2 × \(\frac{2}{5}\)= \(\frac{2}{5}+\frac{2}{5}\) = \(\frac{4}{5}\)

(प्रयास कीजिए पृष्ठ 34-II)

प्रश्न 1.
ज्ञात कीजिए:
(i) 5 × 2\(\frac{3}{7}\)
हल:

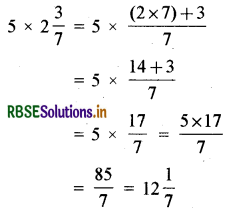
(ii) 1\(\frac{4}{9}\) × 6
हल:

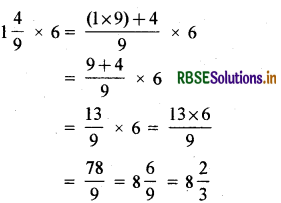
(प्रयास कीजिए पृष्ठ 35)

प्रश्न क्या आप बता सकते हैं कि
(i) 10 का \(\frac{1}{2}\)
हल:
10 का \(\frac{1}{2}\) = \(\frac{1}{2}\) × 10 = \(\frac{10}{2}\) = 5

(ii) 16 का \(\frac{1}{4}\)
हल:
16 का \(\frac{1}{4}\) = \(\frac{1}{4}\) × 16 = \(\frac{16}{4}\) = 4

(iii) 25 का \(\frac{2}{5}\), क्या है?
हल:
25 का \(\frac{2}{5}\) = \(\frac{2}{5}\) × 25 = \(\frac{2 \times 25}{5}\) = \(\frac{50}{5}\) = 10

(प्रयास कीजिए पृष्ठ 39)

प्रश्न 1.
निम्नलिखित बक्सों को भरिए:
हल:

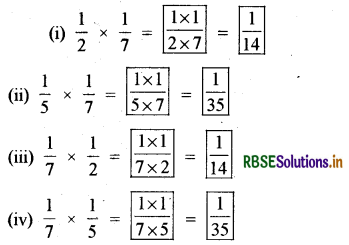
(प्रयास कीजिए पृष्ठ 40-I)

प्रश्न 1.
ज्ञात कीजिए- \(\frac{2}{3} \times \frac{4}{5}; \frac{2}{3} \times \frac{1}{5}\)
हल:

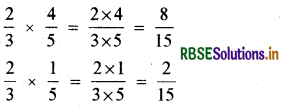
(प्रयास कीजिए पृष्ठ 40-II)

प्रश्न 1.
ज्ञात कीजिए: \(\frac{8}{3} \times \frac{4}{7} ; \frac{3}{4} \times \frac{2}{3}\)
हल:

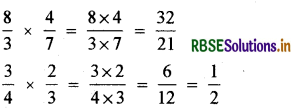
(सोचिए, चर्चा कीजिए एवं लिखिए पृष्ठ 44)

प्रश्न 1.
(i) क्या एक उचित भिन्न का व्युत्क्रम भी उचित भिन्न होगी?
(ii) क्या एक विषम भिन्न का व्युत्क्रम भी एक विषम भिन्न होगा?
हल:
(i) नहीं, इसे निम्न प्रकार स्पष्ट कर सकते हैं-
माना एक उचित भिन्न \(\frac{3}{4}\) है।
इसका व्युत्क्रम \(\frac{4}{3}\) है जो कि एक उचित भिन्न नहीं हैं |
इस प्रकार से उचित भिन्न का व्युत्क्रम एक उचित भिन्न नहीं होगी।

(ii) नहीं, इसे निम्न प्रकार स्पष्ट कर सकते हैंमाना एक विषम भिन्न \(\frac{8}{5}\) है।
इसका व्युत्क्रम में होगा। यह एक विषम भिन्न नहीं \(\frac{5}{8}\) है।

(प्रयास कीजिए पृष्ठ 45-I)

प्रश्न 1.
ज्ञात कीजिए:
(i) 7 ÷ \(\frac{2}{5}\)
हल:

(ii) 6 ÷ \(\frac{4}{7}\)
हल:

(iii) 2 ÷ \(\frac{8}{9}\)
हल:

(प्रयास कीजिए पृष्ठ 45-II)

प्रश्न 1.
ज्ञात कीजिए:
(i) 6 ÷ 5\(\frac{1}{3}\)
हल:

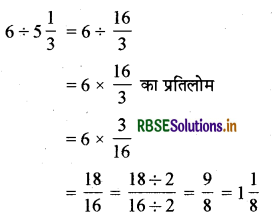
(ii) 7 ÷ 2\(\frac{4}{7}\)
हल:

(प्रयास कीजिए पृष्ठ 46)

प्रश्न 1.
ज्ञात कीजिए:
(i) \(\frac{3}{5} \div \frac{1}{2}\)
हल:

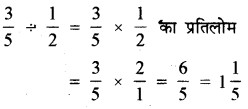
(ii) \(\frac{1}{2} \div \frac{3}{5}\)
हल:

(iii) 2 \(\frac{1}{2} \div \frac{3}{5}\)
हल:

(iv) 5\(\frac{1}{6} \div \frac{9}{2}\)
हल:

(प्रयास कीजिए पृष्ठ 51)

प्रश्न 1.
ज्ञात कीजिए:
(i) 2.7 × 4
हल:
27 × 4 = 108 अतः 2.7 × 4 = 10.8

(ii) 1.8 × 1.2
हल:
18 × 12 = 216 अतः . 1.8 × 1.2 = 2.16

(iii) 2.3 × 4.35
हल:
23 × 435 = 10005 अतः 2.3 × 4.35 = 10.005

प्रश्न 2.
प्रश्न 1 में प्राप्त गुणनफलों को अवरोही क्रम में क्रमबद्ध कीजिए।
हल:
10.8, 2.16 तथा 10.005 का अवरोही क्रम चूंकि 10 > 2
अतः 10.8 > 2.16
10.8 और 10.005 में, दशांश के स्थान के अंकों 8 और 0 में, 8 > 0
अतः 10.8 > 10.005
अतः अवरोही क्रम में
10.8 > 10.005 > 2.16

(प्रयास कीजिए पृष्ठ 52)

प्रश्न 1.
ज्ञात कीजिए:
(i) 0.3 × 10
हल:
0.3 × 10 = 3

(ii) 1.2 × 100
हल:
1.2 × 100 = 120

(iii) 56.3 × 1000
हल:
56.3 × 1000 = 56300

(प्रयास कीजिए पृष्ठ 53)

प्रश्न 1.
ज्ञात कीजिए:
(i) 235.4 ÷ 10
हल:
235.4 ÷ 10 = 23.54

(ii) 235.4 ÷ 100
हल:
235.4 ÷ 100 = 2.354

(iii) 235.4 ÷ 1000
हल:
235.4 ÷ 1000 = 0.2354

(प्रयास कीजिए पृष्ठ 54)

प्रश्न 1.
(i) 35.7 ÷ 3 = ?
हल:

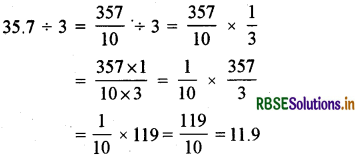
(ii) 25.5 ÷ 3 = ?
हल:

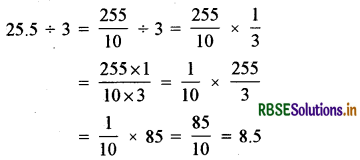
(प्रयास कीजिए पृष्ठ 54-II)

प्रश्न 1.
(i) 43.15 ÷ 5 = ?
हल:

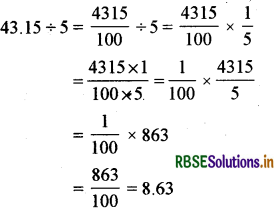
(ii) 82.44 ÷ 6 = ?
हल:

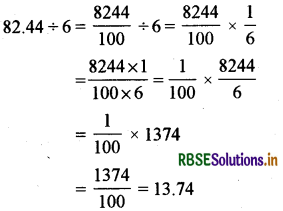
(प्रयास कीजिए पृष्ठ 55)

प्रश्न 1.
ज्ञात कीजिए:
(i) 15.5 ÷ 5
हल:

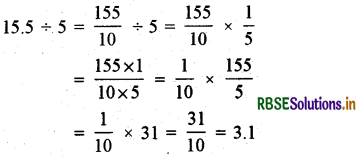
(ii) 126.35 ÷ 7
हल:

(प्रयास कीजिए पृष्ठ 56)

प्रश्न 1.
ज्ञात कीजिए:
(i) \(\frac{7.75}{0.25}\)
हल:

(ii) \(\frac{42.8}{0.02}\)
हल:

(iii) \(\frac{5.6}{1.4}\)
हल: