RBSE Solutions for Class 7 Maths Chapter 2 भिन्न एवं दशमलव Ex 2.1

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 2 भिन्न एवं दशमलव Ex 2.1 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 2 भिन्न एवं दशमलव Ex 2.1

प्रश्न 1.
हल कीजिए:
(i) 2 - \(\frac{3}{5}\)
Answer:

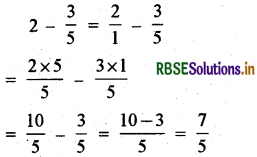
(ii) 4 + \(\frac{7}{8}\)
Answer:

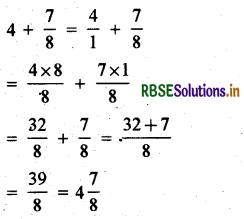
(iii) \(\frac{3}{5}+\frac{2}{7}\)
Answer:

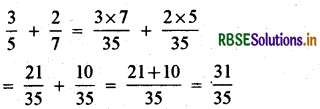
(iv) \(\frac{9}{11}-\frac{4}{15}\)
Answer:
\(\frac{9}{11}-\frac{4}{15}\) हरों 11 और 15 का ल.स. 165 है।
अतः दी गई भिन्नों को तुल्य भिन्नों में बदलते हैं जिनका हर 165 हो।

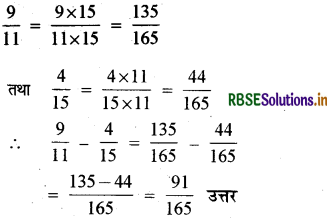
(v) \(\frac{7}{10}+\frac{2}{5}+\frac{3}{2}\)
Answer:
\(\frac{7}{10}+\frac{2}{5}+\frac{3}{2}\) यहाँ हरों 10, 5 और 2 का ल.स. 10 है।
अतः दी गई भिन्नों को तुल्य भिन्नों में बदलते हैं जिनका हर 10 हो।

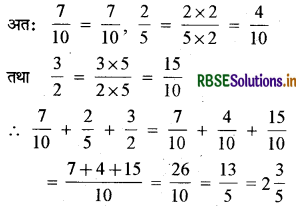
(vi) 2 \(\frac{2}{3}+3 \frac{1}{2}\)
Answer:

(vii) 8 \(\frac{1}{2}-3 \frac{5}{8}\)
Answer:

प्रश्न 2.
निम्नलिखित को अवरोही क्रम में रखिए:
(i) \(\frac{2}{9}, \frac{2}{3}, \frac{8}{21}\)
(ii) \(\frac{1}{5}, \frac{3}{7}, \frac{7}{10}\)
हल:
सबसे पहले इन्हें तुल्य भिन्न में परिवर्तित करेंगे। इसके लिए पहले इनके हरों का ल.स. ज्ञात करते हैं।

(i)

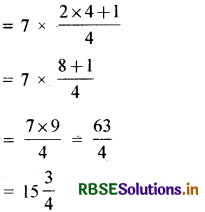
(ii)

प्रश्न 3.
एक 'जादुई वर्ग' में प्रत्येक पंक्ति, प्रत्येक स्तम्भ एवं प्रत्येक विकर्ण की संख्याओं का योग समान होता है। क्या यह एक जादुई वर्ग है?

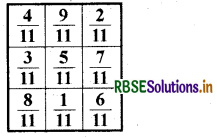
(प्रथम पंक्ति के अनुदिश \(\frac{4}{11}+\frac{9}{11}+\frac{2}{11}=\frac{15}{11}\))
हल:

इस प्रकार, प्रत्येक पंक्ति, स्तम्भ तथा विकर्ण के योग समान हैं।
अतः यह एक जादुई वर्ग है।

प्रश्न 4.
एक आयताकार कागज की लम्बाई 12\(\frac{1}{2}\) cm और चौड़ा 10\(\frac{2}{3}\) cm है। कागज का परिमाप ज्ञात कीजिए।
हल:
आयत का परिमाप = 2 × (लम्बाई + चौड़ाई)

प्रश्न 5.
दी हुई आकृति में, (i) ∆ABE (ii) आयत BCDE, का परिमाप ज्ञात कीजिए। किसका परिमाप ज्यादा है?

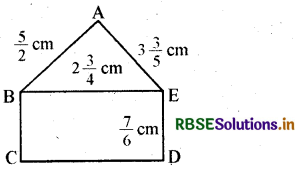
हल:
(i) ∆ABE का परिमाप
= (AB + BE + EA)

(ii) आयत BCDE का परिमाप

चूँकि 8\(\frac{17}{20}\) > 7\(\frac{5}{6}\), इसलिए, त्रिभुज ABE का परिमाप, आयत BCDE के परिमाप से ज्यादा है।

प्रश्न 6.
सलील एक तस्वीर को किसी फ्रेम (चौखट ) में जड़ना चाहता है। तस्वीर 7\(\frac{3}{5}\) cm चौड़ी है। चौखट में उचित रूप से जड़ने के लिए तस्वीर की चौड़ाई 7\(\frac{3}{10}\) cm से ज्यादा नहीं हो सकती। तस्वीर की कितनी काट-छाँट की जानी चाहिए?
हल:
तस्वीर की चौड़ाई = 7\(\frac{3}{5}\) cm
फ्रेम की चौड़ाई = 7\(\frac{3}{10}\) cm
इसे फ्रेम में फिट करने के लिए काट-छाँट करनी चाहिए।

प्रश्न 7.
रीतू ने एक सेब का \(\frac{3}{5}\) भाग खाया और शेष सेब उसके भाई सोमू ने खाया। सेब का कितना भाग सोमू ने खाया? किसका हिस्सा ज्यादा था? कितना ज्यादा था?
हल:
सोमू ने खाया = 1 - \(\frac{3}{5}\)
= \(\frac{5}{5}-\frac{3}{5}\) = \(\frac{2}{5}\)
चूँकि \(\frac{3}{5}\) > \(\frac{2}{5}\) अतः रीतू का हिस्सा ज्यादा था।
उसने \(\left(\frac{3}{5}-\frac{2}{5}\right)\) = \(\frac{1}{5}\) भाग ज्यादा खाया।

प्रश्न 8.
माइकल ने एक तस्वीर में रंग भरने का कार्य \(\frac{7}{12}\) घण्टे में समाप्त किया। वैभव ने उसी तस्वीर में रंग भरने का कार्य \(\frac{3}{4}\) घण्टे में समाप्त किया। किसने ज्यादा समय कार्य किया? यह समय कितना ज्यादा था?
हल:
माइकल ने तस्वीर को रंगा = \(\frac{7}{12}\) घण्टे में
वैभव ने उसी तस्वीर को रंगा = \(\frac{3}{4}\) घण्टे
या \(\frac{3 \times 3}{4 \times 3}=\frac{9}{12}\) घण्टे में
चूँकि \(\frac{9}{12}\) > \(\frac{7}{12}\)
अतः वैभव ने अधिक समय कार्य किया
= \(\frac{9}{12}-\frac{7}{12}\) = \(\frac{2}{12}\) घण्टे = \(\frac{1}{6}\) घण्टे
वैभव ने \(\frac{1}{6}\) घण्टे अधिक कार्य किया।