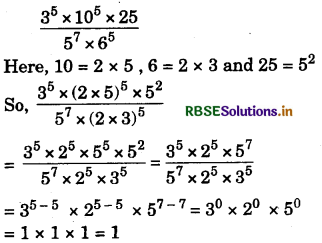RBSE Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.2

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.2 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 13 Exponents and Powers Ex 13.2

Question 1.
Using laws of exponents, simplify and write the answer in exponential form:
(i) 3² × 3⁴ × 3⁸
Answer:
3² × 3⁴ × 3⁸ = 3^{2 + 4 + 8} = 3¹⁴ (Applying a^m × aⁿ = a^{m + n})

(ii) 6¹⁵ ÷ 6¹⁰
Answer:
6¹⁵ ÷ 6¹⁰ = 6^{15 - 10} = 6⁵
(Applying a^m ÷ aⁿ = a^{m - n})

(iii) a³ × a²
Answer:
a³ × a² = a^{3 + 2} = a⁵
(Applying a^m × aⁿ = a^{m + n})

(iv) 7^x × 7²
Answer:
7^x × 7² = 7^{x + 2}
(Applying a^m × aⁿ = a^{m + n})

(v) (5²)³ ÷ 5³
Answer:
(5²)³ ÷ 5³ = 5^{2 × 3} ÷ 5³
(Applying (a^m)ⁿ = a^mn and a^m ÷ aⁿ = a^{m - n})
= 5⁶ ÷ 5³ = 5^{6 - 3} = 5³

(vi) 2⁵ × 5⁵
Answer:
2⁵ × 5⁵ = (2 × 5)⁵ = 10⁶
(Applying a^m × aⁿ = ab^m)

(vii) a⁴ × b⁴
Answer:
a⁴ × b⁴ = (a × b)⁴ = (ab)⁴
(Applying a^m × aⁿ = ab^m)

(viii) (3⁴)⁸
Answer:
(3⁴)⁸ = 3^{4 × 3} = 3¹²
(Applying (a^m)ⁿ = a^mn)

(ix) (2²⁰ ÷ 2¹⁵) × 2³
Answer:
(2²⁰ ÷ 2¹⁵) × 2³ = 2^{20 - 15} × 2³
(Applying a^m ÷ aⁿ = a^{m - n} and a^m × aⁿ = a^{m + n})

(x) 8^t ÷ 8²
Answer:
8^t ÷ 8² = 8^t-2
(Applying a^m ÷ aⁿ = a^{m - n})

Question 2.
Simplify and express each of the following in exponential form:
(i) \(\frac{2^{3} \times 3^{4} \times 4}{3 \times 32}\)
Answer:

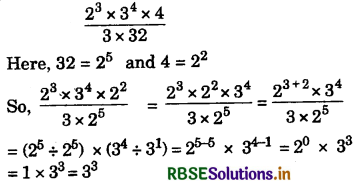
(ii) [(5²)³ × 5⁴] ÷ 5⁷
Answer:
(5²)³ × 5⁴] ÷ 5⁷ = (5⁶ × 5⁴) ÷ 5⁷ = 5^{6 + 4} ÷ 5⁷
= 5¹⁰ ÷ 5⁷
= 5^{10 - 7}
= 5³

(iii) 25⁴ ÷ 5³
Answer:
25⁴ ÷ 5³
Here, 25 = 5²
So, (5²)⁴ ÷ 5³ = 5⁸ ÷ 5³ = 5^{8 - 3} = 5⁵

(iv) \(\frac{3 \times 7^{2} \times 11^{8}}{21 \times 11^{3}}\)
Answer:

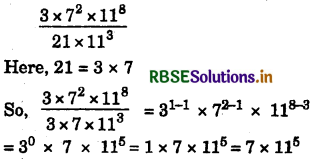
(v) \(\frac{3^{7}}{3^{4} \times 3^{3}}\)
Answer:
\(\frac{3^{7}}{3^{4} \times 3^{3}}\) = \(\frac{3^{7}}{3^{4+3}}\) = \(\frac{3^{7}}{3^{7}}\) = 3^{7 - 7} = 3⁰ = 1

(vi) 2⁰ + 3⁰ + 4⁰
Answer:
2⁰ + 3⁰ + 4⁰
Applying a⁰ = 1
2⁰ + 3⁰ + 4⁰ = 1 + 1 + 1 = 3

(vii) 2⁰ × 3⁰ × 4⁰
Answer:
2⁰ × 3⁰ × 4⁰
Applying a⁰ = 1
2⁰ × 3⁰ × 4⁰ = 1 × 1 × 1 = 1

(viii) (3⁰ + 2⁰) × 5⁰
Answer:
(3⁰ + 2⁰) × 5⁰
Applying a⁰ = 1
(3⁰ + 2⁰) × 5⁰ = (1 + 1) × 1
= 2 × 1 = 2

(ix) \(\frac{2^{8} \times a^{5}}{4^{3} \times a^{3}}\)
Answer:

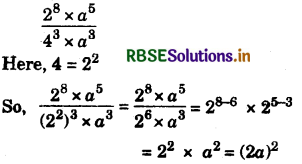
(x) \(\left[\frac{a^{5}}{a^{3}}\right] \)× a⁸
Answer:
\(\left[\frac{a^{5}}{a^{3}}\right]\) × a⁸ = [a^{5 - 3}] × a⁸ = a² × a⁸
= a² + 8 = a¹⁰

(xi) \(\frac{4^{5} \times a^{8} b^{3}}{4^{5} \times a^{5} b^{2}}\)
Answer:
\(\frac{4^{5} \times a^{8} b^{3}}{4^{5} \times a^{5} b^{2}}\) = 4^{5 - 5} × a^{8 - 5} × b^{3 - 2}
= 4⁰ × a³ × b¹ = a³b

(xii) (2³ × 2)²
Answer:
(2³ × 2)² = (2³⁺¹)² = (2⁴)² = 2^{4 × 2} = 2⁸

Question 3.
Say true or false and justify your answer:
(i) 10 × 10¹¹ = 100¹¹
Answer:
10 × 10¹¹ = 100¹¹
∵ 10 × 10u= 101+11= 1012
But 10¹² ≠ 100¹¹
∴ 10 × 1011 10011
So, it is false.

(ii) 2³ > 5²
Answer:
2³ > 5²
2³ = 2 × 2 × 2 = 8
5² = 5 × 5 = 25 and 8 < 25
∴ 2³ < 5²
So, it is false.

(iii) 2³ × 3² = 6⁵
Answer:
2³ × 3² = 6⁵
L.H.S. = 2³ × 3² = 2 × 2 × 2 × 3 × 3 = 72 and
R.H.S. = 6⁵ = 6 × 6 × 6 × 6 × 6 = 7776
72 ≠ 7776
∴ 2³ × 3² ≠ 6⁵
So, it is false.

(iv) 3⁰ = (1000)⁰
Answer:
3⁰ = (1000)⁰
Here, 3⁰= 1 and (1000)⁰ = 1
So, 3⁰ = (1000)⁰
So, it is true.

Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
Answer:
108 × 192
Here, 108 = 2 × 2 × 3 × 3 × 3
(By prime factorization)
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
108 × 192 = (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (2² × 3³) × (2⁶ × 3) = 2^{2 + 6} × 3^{3 + 1} = 2⁸ × 3⁴

(ii) 270
Answer:
270
Here, 270 = 2 × 3 × 3 × 3 × 5 = 2 × 3³ × 5

(iii) 729 × 64
Answer:
729 × 64
Here, 729 = 3 × 3 × 3 × 3 × 3 × 3
64 = 2 × 2 × 2 × 2 × 2 ×2
∴ 729 ×64 = (3 × 3 × 3 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2) = 3⁶ × 2⁶

(iv) 768
Answer:
768
Here, 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁸ × 3¹ = 2⁸ × 3

Question 5.
Simplify:
(i) \(\frac{\left(2^{5}\right)^{2} \times 7^{8}}{8^{3} \times 7}\)
Answer:

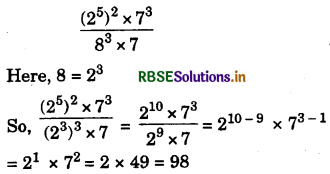
(ii) \(\frac{25 \times 5^{2} \times t^{8}}{10^{3} \times t^{4}}\)
Answer:

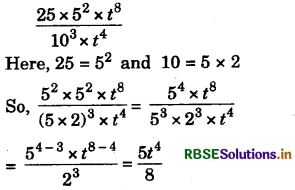
(iii) \(\frac{3^{5} \times 10^{5} \times 25}{5^{7} \times 6^{5}}\)
Answer: