RBSE Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 13 Exponents and Powers Ex 13.1

Question 1.
Find the value of:
(i) 2⁶
Answer:
2⁶ = 2 × 2 × 2 ×2 × 2 × 2 = 64

(ii) 9³
Answer:
9³ = 9 × 9 × 9 = 729

(iii) 11²
Answer:
11² = 11 × 11 = 121

(iv) 5⁴
Answer:
5⁴ = 5 × 5 × 5 × 5 = 625

Question 2.
Express the following in exponential form:
(i) 6 × 6 × 6 × 6
Answer:
6 × 6 × 6 × 6 = 6⁴

(ii) t × t
Answer:
t × t = t²

(iii) b × b × b × b × b
Answer:
b × b × b × b = b⁴

(iv) 5 × 5 × 7 × 7 × 7
Answer:
5 × 5 × 7 × 7 × 7 = 5² × 7³

(v) 2 × 2 × a × a
Answer:
2 × 2 × a × a = 2² × a⁴ = (2a)²

(vi) a × a × a × c × c × c × c × d
Answer:
a × a × a × c × c × c × c × d = a³ × c⁴ × d

Question 3.
Express each of the following numbers using exponential notation :
(i) 512
Answer:
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁹

(ii) 343
Answer:
343 = 7 × 7 × 7 = 7³

(iii) 729
Answer:
729 = 3 × 3 × 3 × 3 × 3 × 3 = 3⁶

(iv) 3125
Answer:
3125 = 5 × 5 × 5 × 5 × 5 = 5⁵

Question 4.
Identify the greater number, wherever possible in each of the following:
(i) 4³ or 3⁴
Answer:
4³ or 3⁴
Since, 4³ = 4 × 4 × 4 = 64
and 3⁴ = 3 × 3 × 3 × 3 = 81
and 64 < 81
So, 4³ < 3⁴

(ii) 5³ or 3⁵
Answer:
5³ or 3⁵
Since 5³ = 5 × 5 × 5 = 125
and 3⁵ = 3 × 3 × 3 × 3 × 3 = 243
and 125 < 243
So, 53 < 35

(iii) 2⁸ or 8²
Answer:
2⁸ or 8²
Since 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
and 8² = 8 × 8 = 64
and 256 > 64
So, 2⁸ > 8²

(iv) 100² or 2¹⁰⁰
Answer:
100² or 2¹⁰⁰
Since 100² = 100 × 100 = 10,000
and 2¹⁰⁰ = (2¹⁰)¹⁰ = (1024)¹⁰ = [1024²]⁵
= [1024 × 1024]⁵ = [1048576]⁵
Since 1048576 > 10,000
So, (1048576)⁵ > 10,000
and 2¹⁰⁰ > 100²

(v) 2¹⁰ or 10²
Answer:
2¹⁰ or 10²
Since 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
and 10² = 10 × 10 = 100
and 1024 >100
So, 2¹⁰ > 10²

Question 5.
Express each of the following as product of powers of their, prime factors: „
(i) 648
Answer:
648

(ii) 405
Answer:
405

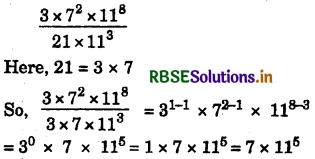
(iii) 540
Answer:
540

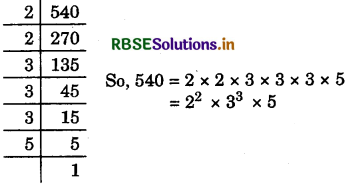
(iv) 3,600
Answer:
3,600

Question 6.
Simplify
(i) 2 × 10³
Answer:
2 × 10³ = 2 × 10 × 10 × 10 = 2 × 1000 = 2000

(ii) 7² × 2²
Answer:
7² × 2² = 7 × 7 × 2 × 2 = 49 × 4 = 196

(iii) 2³ × 5
Answer:
2³ × 5 = 2 × 2 × 2 × 5 = 8 × 5 = 40

(iv) 3 × 4⁴
Answer:
3 × 4⁴ = 3 × 4 × 4 × 4 × 4 = 3 × 256 = 768

(v) 0 × 10²
Answer:
0 × 10² = 0 × 10 × 10 = 0 × 100 = 0

(vi) 5² × 3³
Answer:
5² × 3³ = 5 × 5 × 3 × 3 × 3 = 25 × 27 = 675

(vii) 2⁴ × 3²
Answer:
2⁴ × 3² = 2 × 2 × 2 × 2 × 3 × 3 = 16 × 9 = 144

(viii) 3² × 10⁴
Answer:
3² × 10⁴ = 3 × 3 × 10 × 10 × 10 × 10 = 9 × 10000 = 90,000

Question 7.
Simplify:
(i) (- 4)³
Answer:
(- 4)³ = (- 4) × (- 4) × (- 4) = - 64

(ii) (- 3) × (- 2)³
Answer:
(- 3) × (- 2)³ = (- 3) × (- 2) × (- 2) × (- 2) = (- 3) × (- 8) = 24

(iii) (- 3)² × (- 5)²
Answer:
(- 3)² × (- 5)² = (- 3) × (- 3) × {- 5) × (- 5) = 9 × 25 = 225

(iv) (- 2)³ × (- 10)³
Answer:
(- 2)³ × (- 10)³
= - 2 × - 2 × - 2 × - 10 × - 10 × - 10
= (- 8) × (-1000) = 8000

Question 8.
Compare the following numbers:
(i) 2.7 × 10¹²; 1.5 × 10⁸
Answer:
2.7 × 10¹²; 1.5 × 10⁸
Since 2.7 × 10¹² = \(\frac{27}{10}\) × 10¹² = 27 × 10¹¹
= 27 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10
= 27,00,00,00,00,000
and 1.5 × 10⁸ = \(\frac{15}{10}\) × 10⁸ = 15 × 10⁷
= 15 × 10 × 10 × 10 × 10 × 10 × 10 × 10
= 15,00,00,000
and 27,00,00,00,00,000 > 15,00,00,000
So, 2.7 × 10¹² > 1.5 × 10⁸

(ii) 4 × 10¹⁴; 3 × 10¹⁷
Answer:
4 × 10¹⁴; 3 × 10¹⁷
4 × 10¹⁴ will have 15 digits and 3 × 10¹⁷ will have 18 digits
and 3 × 10¹⁷ will have 18 digits
So, 3 × 10¹⁷ > 4 × 10⁴
(A number containing more digits is greater.)