RBSE Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Intext Questions
Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Intext Questions Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 7. Students can also read RBSE Class 7 Maths Important Questions for exam preparation. Students can also go through RBSE Class 7 Maths Notes to understand and remember the concepts easily. Students can access the data handling class 7 extra questions with answers and get deep explanations provided by our experts.
RBSE Class 7 Maths Solutions Chapter 12 Algebraic Expressions Intext Questions
(Try These - Page 230)
Question 1.
Describe how the following expressions are obtained:
7xy + 5, 3x2y, 4x2 - 5x
Answer:
(i) 7xy + 5
We first multiply two variables x and y, i.e. x × y = xy. Then we .multiply product by a constant 7 to get 7xy. Next we add 5 to 7xy to obtain 7xy + 5.
(ii) x2y
First the variable x is multiplied by itself, i.e. x × x = x2. Then multiply x2 by y to get x2y.
(iii) 4x2 - 5x
First the variable x is multiplied by itself, i.e. x × x = x2. Then multiply x2 by a constant 4, i.e. x2 × 4 = 4x2. Next, we multiply the variable x by a constant 5, i.e. x × 5 = 5x. Now, we subtract 5x from 4x2 to get 4x2 - 5x.

(Try These - Page 231)
Question 1.
What are the terms in the following expressions? Show how the terms are are formed ? Draw a tree diagram for each expression:
8y + 3x2, 7mn - 4, 2x2y
Answer:
(i) 8y + 3x2 Terms are 8y and 3x2.
The term 8y is formed by multiplying the variable y by constant 8.
Then term 3x2 is formed by first multiplying the variable x with itself to get x × x = x2 and term multiplying x2 by 3.
Tree diagram:
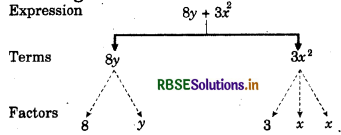
(ii) 7mn - 4
Terms are 7mn and - 4.
The term 7mn is formed by first multiplying variable m and n to get m × n = mn, then multiplying mn by constant 7 to get 7 × mn = 7mn. ,
The term - 4 is a constant.
Tree diagram:
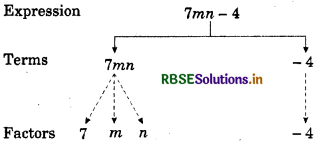
(iii) 2x2y
This expression has only one term to form 2x2y. First we multiply the variable x by itself to get x × x = x2, then x2 is multiplied by another variable y to get x2 + y = x2y, next this product x2y is multiplied by constant 2 to get 2x2y.
Tree diagram:
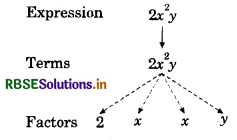
Question 2.
Write three expression each having 4 terms.
Answer:
Expression having 4 terms
- x2 + xy - 2x + 3
- 3x2 + x - 2y - 1
- - 5xy + 3x2 - y2 - x

(Try These - Page 231)
Question 1.
Identify the coefficients of the terms of the following expressions :
4x - 3y, a + b + 5, 2y + 5, 2xy.
Answer:
(i) 4x - 3y
- The coefficient of x in 4x is 4.
- The coefficient of y in - 3y is - 3.
(ii) a + b + 5
- The coefficient of a is then a is 1.
- The coefficient of b in term 6 is 1.
- The coefficient of 5 in term 5 is 1.
(iii) 2y + 5
- The coefficient of y in term 2y is 2.
- The coefficient of 5 in term 5 is 1.
(iv) 2xy
The coefficient of xy in 2xy is 2.
(Try These - Page 233)
Question 1.
Group the like terms together from the following:
12x, 12, - 25x, - 25, - 25y, 1, x, 12y, y
Answer:
25x, x and 12x are the like terms; - 25y, 12y and y are the like terms; 12, - 25 and 1 are like terms.
(Try These - Page 233)
Question 1.
Classify the following expressions as a monomial, a binomial or a trinomial: a, a + b, ab + a + b, ab + a + b - 5, xy, xy + 5, 5x2 - x + 2, 4pq - 3q + 5p, 7, 4m - 7n + 10, 4mn + 7.
Answer:
|
a |
monomial |
|
a + b |
binomial |
|
ab + a + b |
trinomial |
|
ab + a + b - 5 |
polynomial |
|
xy |
monomial |
|
xy + 5 |
binomial |
|
5x2 - x + 2 |
trinomial |
|
4pq - 3q + 5p |
trinomial |
|
7 |
monomial |
|
4m - 7n + 10 |
trinomial |
|
4mn + 7 |
binomial |
(Try These - Page 236)
Question 1.
Think of at least two situations in each of which you need to form two algebraic expressions and add or subtract them.
Answer:
- Ram has thrice the number of book Shaym has. Vinod has 10 books more than twice the number of books Ram and Shyam together have. Find the number of books that Vinod has.
- Rohan’s per month salary is twice the per month salary of Abha. Kavya’s per month salary is ₹ 1000 more than the sum of Rohan’s and Abha’s per month salary. What is the per month salary of Kavya?
(Try These - Page 238)
Question 1.
Add and subtract:
(i) m - n, m + n
(ii) ran + 5 - 2, mn + 3
Answer:
(i) Addition of m - n and m + n
= m - n + m + n - m + m + n - n
= 2m + 0
= 2m
Subtraction of m + n from m - n
= (m - n) - (m + n)
= (m - n) + (- m - n)
= m - n - m - n
= m - m - n-n = 0 - 2n = -2n
(ii) Addition of mn + 5 - 2 and mn + 3
= mn + 5 - 2 + mn + 3
= mn + mn + 5 - 2 + 3
= 2 mn + 6
Subtraction of mn + 3 from mn + 5 - 2
= (mn + 5 - 2) - (mn + 3)
(mn + 5 - 2) + (- mn - 3)
= mn + 5 - 2 - mn - 3
= mn - mn + 5 - 2 - 3
= 0 + 0 = 0
Note: Subtracting a term is the same as adding its inverse. Subtracting - 10b is the same as adding + 10b.
(Try These - Page 245)
Question 1.
Make similar pattern with basic figures as shown:

(The number of segments required to make the figure is given to the right. Also, the expression for the number of segments required to make n shapes is also given.)
Go ahead and discover more such patterns,
Answer:
Some more such patterns are as follow:
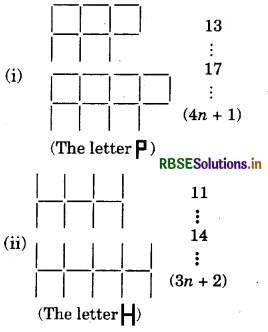

- RBSE Solutions for Class 7 Maths Chapter 8 Comparing Quantities Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Intext Questions
- RBSE Class 7 Maths Notes in Hindi & English Medium Pdf Download
- RBSE Class 7 Maths Important Questions in Hindi & English Medium
- RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Ex 12.2
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 9 परिमेय संख्याएँ Ex 9.1
- RBSE Solutions for Class 7 Maths Chapter 4 सरल समीकरण Ex 4.3
- RBSE Class 7 Maths Important Questions Chapter 13 घातांक और घात