RBSE Solutions for Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल Ex 11.4

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल Ex 11.4 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.4

प्रश्न 1.
एक बगीचा 90 m लम्बा और 75 m चौड़ा है। इसके बाहर, चारों ओर एक 5 m चौड़ा पथ बनाना है। पथ का क्षेत्रफल ज्ञात कीजिए। बगीचे का क्षेत्रफल हेक्टेयर में भी ज्ञात कीजिए।
हल:
माना ABCD एक बगीचा है और PQRS पथ की बाहरी चारदीवारी है।

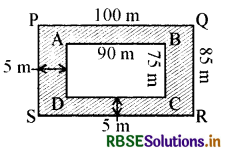
AB = 90 m
AD = 75 m
PQ = (90 + 5 + 5) m = 100 m
और QR = (75 + 5 + 5) = 85 m
अब, पथ का क्षेत्रफल = PQRS का क्षेत्रफल - ABCD का क्षेत्रफल
= (100 × 85 - 90 × 75) m²
= (8500 - 6750) m
= 1750 m2 उत्तर बगीचे का क्षेत्रफल
= ABCD का क्षेत्रफल
= (90 × 75) m²
= 6750 m²
= \(\frac{6750}{10000}\) हेक्टेयर = 0.675 हेक्टेयर

प्रश्न 2.
125 m लम्बाई और 65 m चौड़ाई वाले एक आयताकार पार्क के चारों ओर बाहर 3 m चौड़ा एक पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए।
हल:
माना ABCD एक आयताकार पार्क है। PQRS बाहरी पथ की चारदीवारी है।

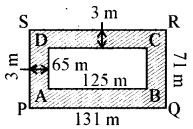
AB = 125 m, AD = 65 m
PQ = (125 + 3 + 3) m
= 131 m और QR = (65 + 3 + 3) m
= 71 m

पथ का क्षेत्रफल = PQRS का क्षेत्रफल - ABCD का क्षेत्रफल
= (131 × 71 - 125 × 65) m²
= (9301 - 8125) m² = 1176 m²

प्रश्न 3.
8 cm लम्बे और 5 cm चौड़े एक गत्ते पर | एक चित्र की पेंटिंग इस प्रकार बनाई गई है कि इसकी प्रत्येक भुजाओं के अनुदिश 1.5 cm चौड़ा हाशिया (margin) छोड़ा गया है। हाशिये का कुल क्षेत्रफल ज्ञात कीजिए।

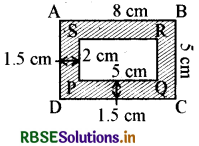
हल:
AB = 8 cm, BC = 5 cm
PQ = (8 - 1.5 - 1.5) cm = 5 cm
PS = (5 - 1.5 - 1.5) cm = 2 cm

हाशिये का क्षेत्रफल = ABCD का क्षेत्रफल - PQRS का क्षेत्रफल
= (8 × 5 - 5 × 2) cm²
= (40 - 10) cm² = 30 cm²

प्रश्न 4.
5.5 m लम्बे और 4 m चौड़े कमरे के चारों ओर बाहर 2.25 m चौड़ा एक बरामदा बनाया गया है। ज्ञात कीजिए:
(i) बरामदे का क्षेत्रफल
(ii) 200 रु. प्रति m' की दर से बरामदे के फर्श पर सीमेंट कराने का व्यय। .

हल:
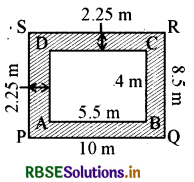
माना ABCD एक कमरा है और माना PORS बाहरी बरामदे की चार दीवारें हैं।
यहाँ, AB = 5.5 m
BC = 4 m
PQ = (5.5 + 2.25 + 2.25) m = 10 m
और QR = (4 + 2.25 + 2.25) m = 8.5 m
(i) बरामदे का क्षेत्रफल = PQRS का क्षेत्रफल - ABCD का क्षेत्रफल
= (10 × 8.5 - 5.5 × 4) m²
= (85 - 22) m² = 63 m²

(ii) 200 रु. प्रति मीटर की दर से बरामदे के फर्श पर सीमेन्ट कराने का व्यय
= (200 × 63) रु. = 12600 रु.

प्रश्न 5.
30 m भुजा वाले एक वर्गाकार बगीचे की परिसीमा से लगा भीतर की ओर 1 m चौड़ा पथ बना हुआ है। ज्ञात कीजिए :
(i) पथ का क्षेत्रफल
(ii) 40 रु. प्रति m² की दर से बगीचे के शेष भाग पर घास लगवाने का व्यय।
हल:
माना ABCD वर्गाकार बगीचे की परिसीमा

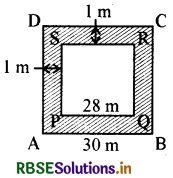
PQRS भीतर के पथ की दीवार है।
यहाँ, AB = 30 m
और PQ = (30 - 1 - 1) m
= 28 m²
पथ का क्षेत्रफल = ABCD का क्षेत्रफल
- PQRS का क्षेत्रफल = (30² - 28²) m
= (30 + 28) (30 - 28) m²
= (58 × 2) m² = 116 m²

(ii) बगीचे के शेष भाग का क्षेत्रफल
= PORS का क्षेत्रफल = (28 × 28) m² = 784 m²
40 रु. प्रति m² की दर से घास लगवाने का व्यय . = (40 × 784) रु. = 31,360 रु.

प्रश्न 6.
700 m लम्बे और 300 m चौड़े एक आयताकार पार्क के मध्य से होकर जाते 10 m चौड़े दो पथ बने हुए हैं जो एक-दूसरे पर परस्पर लम्ब और चौपड़ के आकार के हैं। इनमें से प्रत्येक पथ का क्षेत्रफल ज्ञात कीजिए तथा पार्क की भुजाओं को छोड़कर पार्क के शेष भाग का भी क्षेत्रफल ज्ञात कीजिए। उत्तर को हेक्टेयर में दीजिए।
हल:
माना ABCD और EFGH दो परस्पर पथ हैं।

सजाव आल इन वन

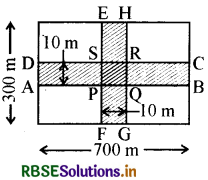
AB = 700 m,
BC = 10 m
∴ ABCD का क्षेत्रफल
= (700 × 10) m
= 7000 m²

पुनः EF = 300 m
और FG = 10 m
∴ EFGH का क्षेत्रफल
= (300 × 10) m² = 3000 m²
यहाँ पथ PQRS दोनों पथों में उभयनिष्ठ है। PQRS का क्षेत्रफल
= (10 × 10) m² = 100 m²

पथों का कुल क्षेत्रफल = पथ ABC का क्षेत्रफल + पथ EFGH का क्षेत्रफल
- PQRS का क्षेत्रफल = (7000 + 3000 - 100) m²
= \(\frac{9900}{10000}\)हेक्टेयर
= 0.99 हेक्टेयर
चौपड़ पथ को छोड़कर पार्क का. क्षेत्रफल = आयताकार पार्क का क्षेत्रफल - सड़कों का क्षेत्रफल
= (700 × 300 - 9900) m² = (210000 - 9900) m²
= 200100 m²
= \(\frac{200100}{10000}\)हेक्टेयर = 20.01 हेक्टेयर

प्रश्न 7.
90 m लम्बाई और 60 m चौड़ाई वाले एक आयताकार मैदान में दो पथ बनाए गए हैं, जो भुजाओं के समान्तर हैं, एक-दूसरे को लम्बवत् काटते हैं और मैदान के मध्य से होकर निकलते हैं। यदि प्रत्येक - पथ की चौड़ाई 3 m हो, तो ज्ञात कीजिए :
(i) पथों द्वारा आच्छादित क्षेत्रफल
(ii) 110 रु. प्रति m² की दर से पथ बनाने का व्यय।
हल:
(i) माना ABCD और EFGH लम्बवत् पथ

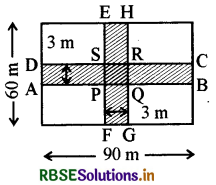
AB = 90 m
और BC = 3 m
∴ ABCD पथ का क्षेत्रफल
= (90 × 3) m²
= 270 m²

पुनः EF = 60 m
और FG = 3 m
∴ EFGH पथ का क्षेत्रफल
= (60 × 3) m² = 180 m²
पथ PQRS दोनों पथों में उभयनिष्ठ है।
PQRS का क्षेत्रफल = (3 × 3) m² = 9 m²
∴ कुल क्षेत्रफल जो पथ के लिए है =ABCD पथ का क्षेत्रफल + पथ EFGH का क्षेत्रफल - PQRS का क्षेत्रफल
= (270 + 180 - 9) m²
= 441 m²

(ii) 110 रु. प्रति mकी दर से पथ बनाने का व्यय
= (110 × 441) रु. = 48510 रु.

प्रश्न 8.
प्रज्ञा 4 cm त्रिज्या वाले एक वृत्ताकार पाइप के चारों ओर एक रस्सी लपेटती है (जैसा दिखाया गया है) और रस्सी की आवश्यक लम्बाई को काट लेती है। इसके बाद वह उसे 4 cm भुजा वाले एक वर्गाकार बॉक्स के चारों ओर लपेटती है (दिखाया गया है)। क्या उसके पास कुछ और रस्सी बचेगी? (π = 3.14)

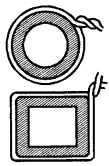
हल:
वृत्ताकार पाइप के चारों ओर लपेटी गई रस्सी की लम्बाई
= पाइप की परिधि
= (2 × 3.14 × 4) cm = 25.12 cm
वर्गाकार बॉक्स के चारों ओर लपेटी गई रस्सी की लम्बाई
= वर्ग का परिमाप = 4 × भुजा = (4 × 4) cm = 16 cm
स्पष्ट है, 25.12 cm > 16 cm
हाँ, (25.12 - 16) cm = 9.12 cm रस्सी प्रज्ञा के पास बचती है।

प्रश्न 9.
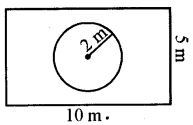
संलग्न आकृति, एक आयताकार पार्क के मध्य में एक वृत्ताकार फूलों की क्यारी को दर्शाती है। ज्ञात कीजिए :
(i) पूरे पार्क का क्षेत्रफल
(ii) फूलों की क्यारी का क्षेत्रफल
(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल
(iv) क्यारी की परिधि।

हल:
(i) पूरे पार्क का क्षेत्रफल
= (10 × 5) m² = 50 m²

(ii) फूलों की क्यारी का क्षेत्रफल 2ur = (2 × 3.14 × 2) m²
= 12.56 m²

(iii) पार्क के शेष भाग का क्षेत्रफल
= (50 - 12.56) m²
= 37.44 m²

(iv) फूलों की क्यारी की परिधि
= (2 × 3.14 × 2) m
= 12.56 m

प्रश्न 10.
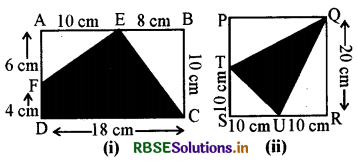
दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए :

हल:
(i) छायांकित भाग DCEFD का क्षेत्रफल = आयत ABCD का क्षेत्रफल - ΔECB का क्षेत्रफल - ΔEAF का क्षेत्रफल
= AB × BC - \(\frac{1}{2}\) × EB : BC - \(\frac{1}{2}\) × AE × AF
= (18 × 10 - \(\frac{1}{2}\) × 8 × 10 - \(\frac{1}{2}\) × 10 × 6) cm²
= (180 - 40 - 30) cm²
= 110 cm²

(i) छायांकित भाग TUQ का क्षेत्रफल = वर्ग PQRS का क्षेत्रफल - (ΔTSU) का क्षेत्रफल - (ΔURQ) का क्षेत्रफल - (ΔTPQ) का क्षेत्रफल
= (PQ)² - \(\frac{1}{2}\) × TS × SU - \(\frac{1}{2}\) × UR × QR - \(\frac{1}{2}\) × PQ × TP)
= (20 × 20 - \(\frac{1}{2}\) × 10 × 10 - \(\frac{1}{2}\) × 10 × 20 - \(\frac{1}{2}\) × 20 × 10) cm²
= (400 - 50 - 100 - 100) cm²
= (400 - 250) cm²
= 150 cm²

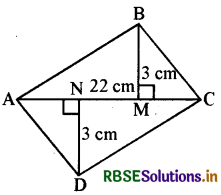
प्रश्न 11.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए। यहाँ AC = 22 cm, BM = 3 cm, DN = 3 cm और BM ⊥ AC, DN ⊥ AC.

हल:
चतुर्भुज ABCD का क्षेत्रफल
= (ΔABC) का क्षेत्रफल + (ΔACD) का क्षेत्रफल
= (\(\frac{1}{2}\) × 22 × 3 × \(\frac{1}{2}\) × 22 × 3)
= (33 + 33) cm²
= 66 cm²