RBSE Solutions for Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल Ex 11.2

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.2

प्रश्न 1.
निम्न में प्रत्येक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए :

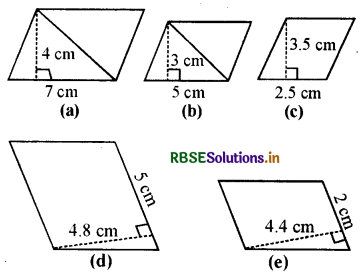
हल:
(a) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (7 × 4) cm²
= 28 cm

(b) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (5 × 3) cm² = 15 cm

(c) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (2.5 × 3.5) cm² = 8.75 cm

(d) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (5 × 4.8) cm² = 24 cm

(e) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (2 × 4.4) cm² = 8.8 cm

प्रश्न 2.
निम्न में प्रत्येक त्रिभुज का क्षेत्रफल ज्ञात कीजिए :

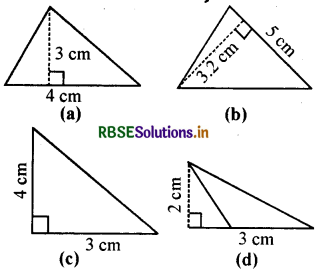
हल:
(a) त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
= (\(\frac{1}{2}\) × 4 × 3) cm² = 6 cm

(b) त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
= (\(\frac{1}{2}\) × 5 ×32) cm² = 8 cm

(c) त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
= (\(\frac{1}{2}\) × 3 × 4) cm² = 6 em

(d) त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
= (\(\frac{1}{2}\) × 3 × 2) cm²
= 3 cm²

प्रश्न 3.
रिक्त स्थान का मान ज्ञात कीजिए :
हल:
हम जानते हैंसमान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई इसलिए रिक्त स्थान की गणना इस प्रकार है :

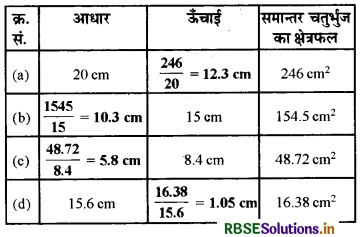
प्रश्न 4.
रिक्त स्थानों का मान ज्ञात कीजिए :
हल:
हम जानते हैं
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई

रिक्त स्थानों का मान इस प्रकार है :

प्रश्न 5.
PQRS एक समान्तर चतुर्भुज है (आकृति देखें)।QM शीर्ष Q से SR तक की ऊँचाई तथा QN शीर्ष से PS तक की ऊँचाई है। यदि SR = 12 cm और OM = 7.6 cm तो ज्ञात कीजिए :
(a) समान्तर चतुर्भुज PORS का क्षेत्रफल
(b) QN, यदि PS = 8 cm

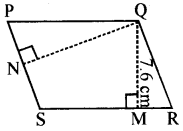
हल:
(a) PQRS समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई = SR × QM = (12 × 7.6) cm² = 91.2 cm²

(b) समान्तर चतुर्भुज PQRS का क्षेत्रफल
= आधार - ऊँचाई इसलिए,
PS × QN = समान्तर चतुर्भुज PQRS का क्षेत्रफल
या 8 × QN = 91.2
या QN = \(\frac{91.2}{8}\) cm = 11.4 cm उत्तर

प्रश्न 6.
DL और BM समान्तर चतुर्भुज ABCD की क्रमशः भुजाएँ AB और AD पर लम्ब हैं ( आकृति देखें)। यदि समान्तर चतुर्भुज का क्षेत्रफल 1470 cm है, AB = 35 cm और AD = 49 cm है, तो BM तथा DL की लम्बाई ज्ञात कीजिए।

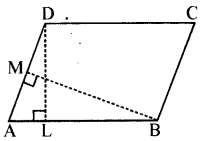
हल:
समान्तर चतुर्भुज ABCD का क्षेत्रफल
= 1470 cm²
AB = 35 cm और AD = 49 cm

समान्तर चतुर्भुज ABCD का क्षेत्रफल
= AD × BM
इसलिए, 1470 = 49 × BM
या BM = \(\frac{1470}{49}\) cm = 30 cm

समान्तर चतुर्भुज ABCD का क्षेत्रफल
- AB × DL
इसलिए, 1470 = 35 × DL
या DL = \(\frac{1470}{35}\)cm = 42 cm

प्रश्न 7.
त्रिभुज ABC,A पर समकोण है ( आकृति देखें), और AD भुजा BC पर लम्ब है। यदि AB = 5 cm, BC = 13 cm और AC = 12 cm है, तो AABC का क्षेत्रफल ज्ञात कीजिए। AD की लम्बाई भी ज्ञात कीजिए। .

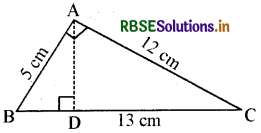
हल:
ΔABC, A पर समकोण है तथा AD भुजा BC पर लम्ब है, इसलिए ΔABC का क्षेत्रफल
= \(\frac{1}{2}\) × AB × AC = (\(\frac{1}{2}\) × 5 × 12) cm
= 30 cm

पुन: ΔABC का क्षेत्रफल
= \(\frac{1}{2}\) × BC × AD
इसलिए, 30 = \(\frac{1}{2}\) × 13 × AD
या AD = \(\frac{2 \times 30}{13}\) cm = \(\frac{60}{13}\) cm

प्रश्न 8.
ΔABC समद्विबाहु त्रिभुज है जिसमें AB = AC = 7.5 cm और BC = 9 cm है (आकृति देखें)। A से BC तक की ऊँचाई AD, 6 cm है। ΔABC का क्षेत्रफल ज्ञात कीजिए।C से AB तक की ऊँचाई, अर्थात् CE क्या होगी?

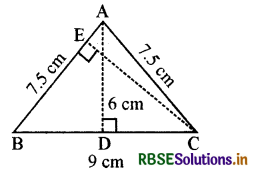
हल:
ΔABC का क्षेत्रफल
= \(\frac{1}{2}\) × BC × AD
= (\(\frac{1}{2}\) × 9 × 6) cm
= 27 cm²

ΔABC का क्षेत्रफल = \(\frac{1}{2}\) × AB × ऊँचाई
इसलिए, 27 = \(\frac{1}{2}\) × 7.5 × C से AB
तक की ऊँचाई अर्थात् CE
या CE = \(\frac{2 \times 27}{7.5}\) = 7.2 cm