RBSE Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 11 Perimeter and Area Ex 11.2

Question 1.
Find the area of each of the following parallelograms:

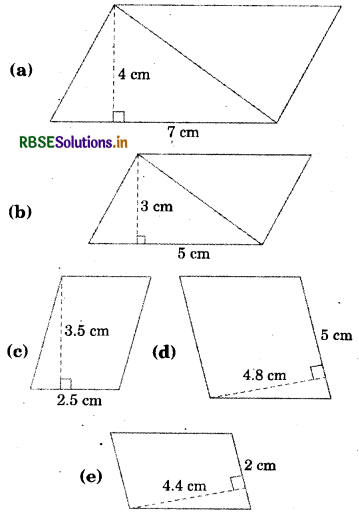
Answer:
Area of parallelogram = base × height
(a) Area = 4 cm × 7 cm = 28 cm²
(b) Area = 5 cm × 3 cm = 15 cm²
(c) Area = 2.5 cm × 3.5 cm = 8.75 cm²
(d) Area = 5 × 4.8 cm = 24 cm²
(e) Area = 2 cm × 4.4 cm = 8.8 cm².

Question 2.
Find the area of each of the following triangles:
(a)

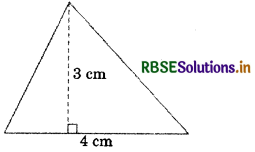
Answer:
Area of triangle = \(\frac{1}{2}\) × base × height
Area = \(\frac{1}{2}\) × 4 × 3 = 6 cm²

(b)

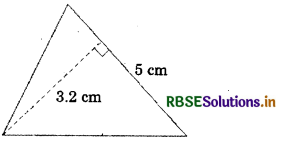
Answer:
Area of triangle = \(\frac{1}{2}\) × base × height
Area = \(\frac{1}{2}\) × 5 × 3.2 = 8 cm²

(c)

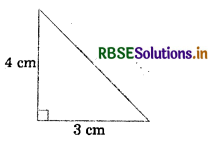
Answer:
Area of triangle = \(\frac{1}{2}\) × base × height
Area = \(\frac{1}{2}\) × 3 × 4 = 6 cm²

(d)

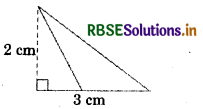
Answer:
Area of triangle = \(\frac{1}{2}\) × base × height
Area = \(\frac{1}{2}\) × 3 × 2 = 3 cm²

Question 3.
Find the missing values:

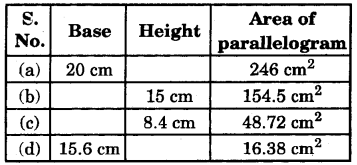
Answer:
(a) Height = \(\frac{\text { Area of parallelogram }}{\text { base }}\)
= \(\frac{246 \mathrm{~cm}^{2}}{20 \mathrm{~cm}}\) = 12.3 cm

(b) Base = \(\frac{\text { Area of parallelogram }}{\text { base }}\)
= \(\frac{154.5 \mathrm{~cm}^{2}}{15 \mathrm{~cm}}\) = 10.3 cm

(c) Base = \(\frac{\text { Area of parallelogram }}{\text { base }}\)
= \(\frac{48.72 \mathrm{~cm}^{2}}{8.4 \mathrm{~cm}}\) = 5.8 cm

(d) Height = \(\frac{\text { Area of parallelogram }}{\text { base }}\)
= \(\frac{16.38 \mathrm{~cm}^{2}}{15.6 \mathrm{~cm}}\) = 1.05 cm

Question 4.
Find the missing values:

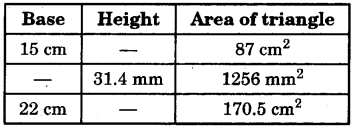
Answer:
(a) Area of triangle = \(\frac{1}{2}\) × base × height
Height of triangle = \(\frac{2 \times \text { Area }}{\text { Base }}\) = \(\frac{2 \times 87}{15}\) = \(\frac{58}{5}\) = 11.6 cm

(b) Base = \(\frac{2 \times \text { Area }}{\text { Base }} \)= \(\frac{2 \times 1256}{31.4}\) = 80 mm

(c) Height = \(\frac{2 \times \text { Area }}{\text { Base }}\) = \(\frac{2 \times 170.5}{22}\) = 15.5 cm.

Question 5.
PQRS is a parallelogram (see fig.). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:

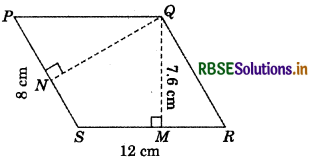
(a) The area of the parallelogram PQRS.
(b) QN, if PS = 8 cm.
Answer:
(a) Area of parallelogram PQRS = base × height
= SR × QM = 12 cm × 7.6 cm = 91.2 cm²

(b) Height QN = \(\frac{\text { Area of parallelogram }}{\text { Base (SP) }}\)
= \(\frac{91.2 \mathrm{~cm}^{2}}{8 \mathrm{~cm}}\) = 11.4 cm

Question 6.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (see fig.). If the area of the parallelogram is 1470 cm2, AB - 35 cm and AD = 49 cm, find the length of BM and DL.

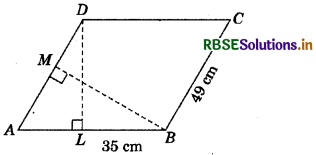
Answer:
Area of parallelogram ABCD
= base × height = AD × BM
⇒ 1470 = 49 × BM
⇒ BM = \(\frac{1470}{49}\) cm = 30 cm.
Hence, the length of BM is 30 cm.
Again, area of parallelogram ABCD
= AB × DL
⇒ 1470 = 35 × DL
⇒ DL = \(\frac{1470}{35}\) cm = 42 cm
Hence, the length of DL is 42 cm.

Question 7.
∆ABC is right-angled at A (see fig.). AD is perpendicular to BC. If AB = 5 cm, BC s 13 cm and AC = 12 cm. Find the area of ∆ABC. Also find the length of AD.

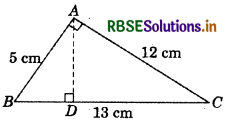
Answer:
Area of AABC = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 5 × 12 cm²
= 30 cm²
Length of height AD = \(\frac{2 \times \text { area of } \Delta A B C}{\text { Base }}\)
= \(\frac{2 \times 30}{13}\) = \(\frac{60}{13}\) cm
= 4.6 cm (approx.)
So, the area of ∆ABC is 30 cm2 and the length of height AD is 4.6 cm (approx.).

Question 8.
∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC is 6 cm. Find the area of ∆ABC. What will be the height from C to AB, i.e., CE?

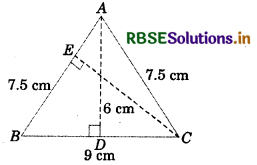
Answer:
Area of ∆ABC = \(\frac{1}{2}\) × (base × height)
= \(\frac{1}{2}\) × BC × AD
= \(\frac{1}{2}\) (9 × 6) cm² = 27 cm²
Hence, the area of ∆ABC is 27 cm².
Again area of ∆ABC = \(\frac{1}{2}\) (base × height)
27 cm² = \(\frac{1}{2}\) (AB × CE)
⇒ 27 cm² = \(\frac{1}{2}\) (7.5 cm × CE)
⇒ CE = \(\frac{2 \times 27 \mathrm{~cm}^{2}}{7.5 \mathrm{~cm}}\) = 7.2 cm
Hence, the height from C to AB is CE is 7.2 cm.