RBSE Solutions for Class 7 Maths Chapter 10 प्रायोगिक ज्यामिती Intext Questions
Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 10 प्रायोगिक ज्यामिती Intext Questions Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 7. Students can also read RBSE Class 7 Maths Important Questions for exam preparation. Students can also go through RBSE Class 7 Maths Notes to understand and remember the concepts easily. Students can access the data handling class 7 extra questions with answers and get deep explanations provided by our experts.
RBSE Class 7 Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Intext Questions
(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 211)
प्रश्न 1.
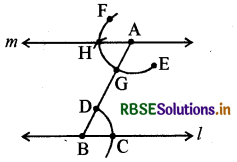
निम्न रचना में, क्या आप A से होकर जाती हुई अन्य रेखा खींच सकते हैं जो । के समान्तर हो।
हल:
नहीं, कोई दूसरी रेखा जो A से होकर जाती हो तथा के समान्तर हो, नहीं खींच सकते हैं। यहाँ केवल एक ही रेखा खींची जा सकती है, जो बिन्दु A और H से होकर जाती है।
प्रश्न 2.
क्या आप इस रचना में इस प्रकार का परिवर्तन कर सकते हैं कि बराबर एकान्तर अन्तःकोण बनाने के स्थान पर बराबर संगत कोण बनें?
हल:
रचना के पद
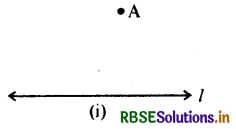
1. एक रेखा खींचेंगे और l के बाहर एक बिन्दु 'A' लेंगे।
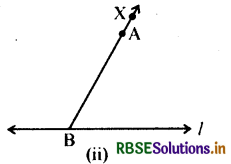
2. l पर दूसरा बिन्दु B लेंगे और BA को मिलायेंगे। इसे X तक बढ़ायेंगे।
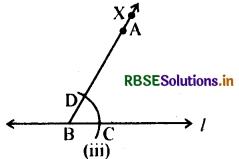
3. B को केन्द्र मानकर उचित त्रिज्या लेकर चाप खींचेंगे जो l को C पर और BX को D पर काटेगी।
4. A को केन्द्र मानकर उसी त्रिज्या से एक चाप EF खींचेंगे जो AX को G पर काटता है।
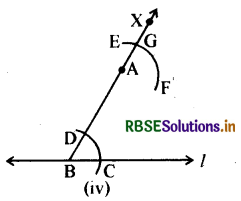
5. परकार को C पर रखेंगे। पेंसिल टिप D पर व्यवस्थित करेंगे।
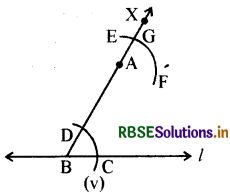
6. पाँचवें चरण के अनुसार G को केन्द्र मानकर चाप खींचेंगे जो EF को H पर काटता है।
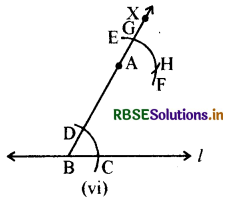
7. AH को मिलाकर रेखा 'm' खींचेंगे।
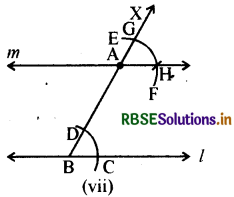
ध्यान दीजिए-∠ABC और ∠GAH संगत कोण हैं।
∴ m ∥ l
(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 214)
प्रश्न 1.
एक विद्यार्थी ने एक ऐसा त्रिभुज खींचने का प्रयत्न किया, जिसकी रफ आकृति यहाँ दी गई है। पहले उसने QR खींचा। फिर उसने Q को केन्द्र मानकर और 3 cm त्रिज्या लेकर एक चाप खींची तथा R को केन्द्र मानकर और 2 cm त्रिज्या लेकर एक अन्य चाप खींची। परन्तु वह P नहीं प्राप्त कर सका। इसका क्या कारण है? इस प्रश्न से सम्बन्धित त्रिभुज के किस गुण को आप जानते हैं? क्या ऐसे त्रिभुज का अस्तित्व है?
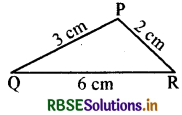
हल:
हम जानते हैं कि किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से सदैव बड़ा होता है। इस त्रिभुज में तीन भुजाओं, जिनकी लम्बाइयाँ दी हुई हैं, में दो भुजाओं की लम्बाई तीसरे से बड़ी है। लेकिन तीसरी स्थिति में 3 + 2 = 5 ≯ 6 यही कारण है P बिन्दु प्राप्त नहीं हो सका।
(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 218)
प्रश्न 1.
ΔABC में, यदि AC = 7 cm, m∠A = 60° और m∠B = 50° है, तो क्या आप त्रिभुज की रचना कर सकते हैं? (त्रिभुज का कोण योग गुण आपकी सहायता कर सकता है।)
हल:
यहाँ पर हमें भुजा AC, ∠A तथा ∠B दिया हुआ है लेकिन त्रिभुज खींचने के लिए ∠C की आवश्यकता है।
त्रिभुज के कोणों के योग के गुण से
∠A + ∠B + ∠C = 180°
इसलिए, 60° + 50° + ∠C = 180°
110° + ∠C = 180° या
∠C = 180° - 110° = 70°
AC = 7cm, ∠A = 60° और
∠C = 70°
इसलिए, हम ΔABC खींच सकते हैं।
विविध प्रश्न
प्रश्न 1.
नीचे कुछ त्रिभुजों की भुजाओं और कोणों के माप दिए गए हैं। इनमें से उनकी पहचान कीजिए, जिनकी रचना नहीं की जा सकती तथा यह भी बताइए कि आप इनकी रचना क्यों नहीं कर सकते? शेष त्रिभुजों की रचना कीजिए।
|
त्रिभुज |
दिए हुए माप |
|
1. ΔABC |
m∠A = 85°, m∠B = 115°, AB = 5 cm |
|
2. ΔPQR |
m∠Q = 30°, m∠R = 60°, QR = 4.7 cm |
|
3. ΔABC |
m∠A = 70°, m∠B = 50°, AC = 3 cm |
|
4. ΔLMN |
m∠L = 60°, m∠N = 120°, LM = 5 cm |
|
5. ΔABC |
BC = 2 cm, AB = 4 cm, AC = 2 cm |
|
6. ΔPQR |
PQ = 3.5 cm, QR = 4 cm, PR = 3.5 cm |
|
7. ΔXYZ |
XY = 3 cm, YZ = 4 cm, XZ = 5 cm |
|
8. ΔDEF |
DE = 4.5 cm, EF = 5.5 cm, DF = 4 cm |
हल:
1. M∠A + m∠B = 85° + 115° = 200° > 180°
लेकिन त्रिभुज में तीनों कोणों का योग 180° होता है।
∴ ΔABC की रचना नहीं हो सकती।
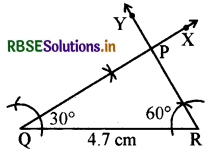
2. ΔPQR बन सकता है।
रचना के चरण
- QR = 4.7 cm की रेखा खींचिए।
- ∠XQR = 30° खींचिए।
- ∠YRQ, Y के एक ही दिशा में खींचिए। ∠YRQ = 60° QX और RY आपस में बिन्दु P पर काटते हैं। तब, ΔPQR ही अभीष्ट त्रिभुज होगा।
3. m∠A, m∠B और भुजा AC दिए हुए हैं।
त्रिभुज ABC खींचने के लिए ∠C की आवश्यकता है।
∠C की माप :
∠A + ∠B + ∠C = 180°
या 70° + 50° + ∠C = 180°
120° + ∠C = 180°
∠C = 180° - 120° = 60°
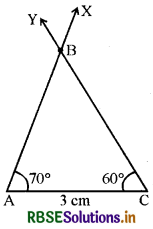
रचना के चरण
- AC = 3 cm का रेखाखण्ड खींचिए।
- ∠CAX = 70° खींचिए।
- ΔACY = 60° खींचिए। AX और CY बिन्दु B पर काटते हैं। इस प्रकार प्राप्त ΔABC ही अभीष्ट त्रिभुज होगा।
4. m∠L + m∠N = 60° + 120° = 180° त्रिभुज के तीनों कोणों का योग 180° होता है।
∴ ΔLMN नहीं बन सकता है।
5. BC + AC = 2 cm + 2 cm = 4 cm ≯ ABI
लेकिन त्रिभुज की दो भुजाओं का योग तीसरी से बड़ा होता है।
∴ भुजा-भुजा-भुजा की रचना का प्रयोग करके, ΔABC की रचना नहीं की जा सकती है।
6. दिया है, PQ = 3.5 cm, QR = 4 cm, PR = 3.5 cm
भुजा-भुजा-भुजा की रचना का प्रयोग करके, ΔPQR की रचना की जा सकती है।
रचना के चरण
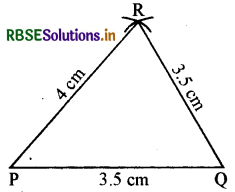
- रेखाखण्ड PQ = 3.5 cm खींचिए ।
- बिन्दु P से परकार की सहायता से 4 cm का चाप काटो।
- बिन्दु Q से 3.5 cm का चाप काटो जो पहले वाले चाप को बिन्दु R पर मिले।
- PR तथा QR को मिलाओ। यही अभीष्ट ΔPQR है।
7. भुजा-भुजा-भुजा की रचना का प्रयोग करके, ΔXYZ की रचना की जा सकती है। [नोट - ऊपर प्रश्न 6 में बतलाये अनुसार रचना करें।]
8. भुजा-भुजा-भुजा की रचना का प्रयोग करके, ऊपर प्रश्न 6 में बतलाये अनुसार ΔDEF की रचना की जा सकती है।
- RBSE Solutions for Class 7 Maths Chapter 8 Comparing Quantities Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Intext Questions
- RBSE Class 7 Maths Notes in Hindi & English Medium Pdf Download
- RBSE Class 7 Maths Important Questions in Hindi & English Medium
- RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Ex 12.2
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 9 परिमेय संख्याएँ Ex 9.1
- RBSE Solutions for Class 7 Maths Chapter 4 सरल समीकरण Ex 4.3
- RBSE Class 7 Maths Important Questions Chapter 13 घातांक और घात