RBSE Solutions for Class 7 Maths Chapter 10 Practical Geometry Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 10 Practical Geometry Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 10 Practical Geometry Intext Questions

(Think, Discuss and Write - Page 195)

Question 1.
In the above construction, can you draw any other line through A that would be also parallel to the line l?
Answer:
No, because through a given point only one line parallel to a given line can be drawn.

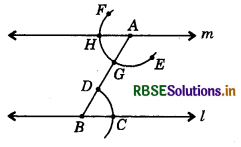
Question 2.
Can you slightly modify the above construction, to use the idea of equal corresponding angles instead of equal alternate angles?
Answer:
Yes

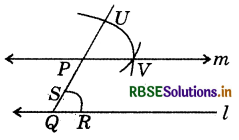
In this, with P as centre and radius equal to QR draw an arc to cut PQ (extended) at U. With centre as U and radius equal to SR mark a point V as shown in the figure. Now join PV to draw a line m, which is parallel to given line l.
Here, the corresponding angles ∠RQU and ∠VPU are equal. Therefore l∥m.

(Think, Discuss and Write - Page 198)

Question 1.
A student attempted to draw a triangle whose rough figure is given here. He drew QR first. Then with Q as centre, he drew an arc of 3 cm and with R centre, he drew an arc of 2 cm. But he could not get P. What is the reason? What property of triangle do you know in connection with this problem? 
Can such a triangle exist? (Remember the property of triangle, “The sum of any two sides of a triangle is always greater than the third side.)
Answer:
In a triangle sum of lengths of any two sides is greater than the third side, Q But here, 2 cm + 3 cm, i.e. 5 cm < 6 cm. So, this triangle does not exist.

(Think, Discuss and Write - Page 202)

Question 1.
In the above example, length of a side and measures of two angles were given. Now study the following problem:
In ΔABC, if AC = 7 cm, m∠A = 60° and m∠B = 50°. Can you draw the triangle? (Angle sum property of a triangle may help you!)
Answer:
Draw line segment AC and ∠A = 60°. Now we will construct ∠C which is not given but using angle sum property of triangle we can find ∠C.

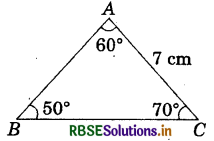
∠C = 180° - (∠B + ∠A)
= 180° - (60° + 50°) = 180° - 110° = 70° 
Now construct ∠C = 70° we will get ΔABC.

(Miscellaneous question - Page 204)

Question 1.
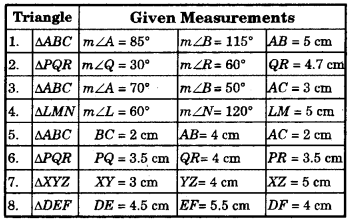
Below are given the measures of certain sides and angles of triangles.
Identify those which cannot be constructed, and say why you cannot construct them? Construct rest of the triangles.

Answer:
1. In given triangle ABC,
m∠A = 85°, m∠B = 115° and AB = 5 cm
In ΔABC, ∠A + ∠B + ∠C = 180°
∠A + ∠B =85°+ 115° =200°
Here, ∠A + ∠B (200°) >180°
So ∠A + ∠B + ∠C will be greater than 180°. 
Thus, ΔABC cannot be constructed.

2. In given triangle PQR, m∠Q = 30°, m∠R = 60° and QR = 4.7 cm.

1. Draw a line segment QR = 4.7 cm.
2. At Q, construct ∠RQX = 30°.
3. At R, construct ∠QRY = 60°.
4. Let QX and RY intersect at P.

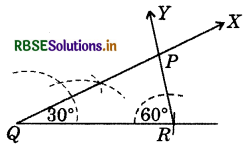
Thus, ΔPQR is the required triangle.

3. In given triangle ABC, m∠A = 70°, m∠B = 50° and AC = 3 cm, we need measure of ∠C to complete triangle.
m∠C = 180° - (∠A + ∠B)
= 180° - (70°+ 50°)
= 180° - 120° = 60°

1. Draw a line segment AC = 3 cm.
2. At A, construct ∠CAX - 70°.
3. At C, construct ∠ACY = 60°.
4. Let the rays AX and CY meet at B.

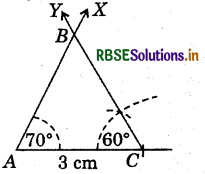
∴ ΔABC is the required triangle.

4. In given triangle LMN, m∠L = 60°, m∠N = 120° and LM = 5 cm.
In ΔLMN, ∠L + ∠M + ∠N = 180°
∠L + ∠M = 60° + 120° = 180°
So, ∠L + ∠M + ∠N > 180°
Thus, ΔLMN cannot be constructed.

5. In given triangle ABC, BC = 2 cm, AB = 4 cm and AC = 2 cm.
A triangle is possible only when the sum of lengths of any two sides is greater than the length of the third side.
Here, BC + AC = 2 cm + 2 cm = 4 cm = AB [AB = 4 cm]
So, ΔABC is not possible.

6. In given triangle PQR, PQ = 3.5 cm, QR = 4 cm and PR = 3.5 cm ,

1. Draw a line segment PQ = 3.5 cm.
2. With centre P and radius 3.5 cm, draw an arc.
3. With centre Q and radius 4 cm, draw another arc, such that it cuts the previous arc at R.
4. (iv) Join RP and RQ.

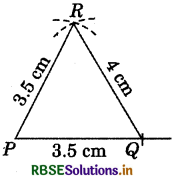
Thus, ΔPQR is the required triangle.

7. In given triangle XYZ, XY = 3 cm, YZ = 4 cm and XZ = 5 cm.

1. Draw a line segment YZ = 4 cm.
2. With centre Y and radius 3 cm, draw an arc.
3. With centre Z and radius 5 cm, draw another arc which cuts the previous arc at X.
4. Join XY and XZ.

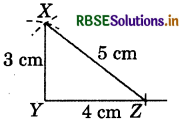
Thus, ΔXYZ is the required triangle.

8. In given triangle DEF, DE = 4.5 cm, EF = 5.5 cm and DF = 4.0 cm.

1. Draw a line segment EF = 5.5 cm.
2. With centre E and radius 4.5 cm, draw an arc.
3. With centre F and radius 4 cm, draw another arc such that it intersects the previous arc at D.
4. Join DE and DF.

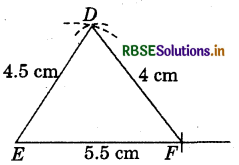
Thus, ΔDEF is the required triangle.