RBSE Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 10 Practical Geometry Ex 10.1

Question 1.
Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
Answer:
Step 1. Draw a line AB, and mark a point C outside it.
Step 2. Mark another point D on AB and join CD.
Step 3. With D as centre and a convenient radius, draw an arc cutting AB at E and CD at F.

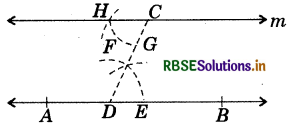
Step 4. With C as centre and radius equal to DE draw an arc, cutting CD at G.
Step 5. With G as centre* and radius (opening) equal to EF, mark a point H on the above arc.
Step 6. Join CH to draw a line ‘m’.
Thus 'm' is the required line such that m ∥ AB.

Question 2.
Draw a line Z. Draw a perpendicular to Z at any point on l. On this perpendicular choose a point X, 4 cm away from Z. Through X, draw a line m parallel to Z.
Sol. : Step 1. Draw a line l, and mark a point A on it.
Step 2. Construct an angle of 90° at A to draw AL perpendicular to l.
Step 3.. Mark a point X on AL such that AX = 4 cm.
Step 4. At X, construct an angle of 90° to draw a perpendicular (m) to AL.

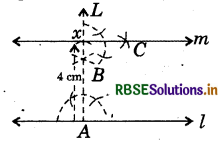
Thus ‘m’ is the required line through X such that m ∥ l.
 
Question 3.
Let Z be a line and P be a point not on Z. Through P, draw a line m parallel to Z. Now join P to any point Q on Z. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet Z as S. What shape do the two sets of parallel lines enclose?
Answer:

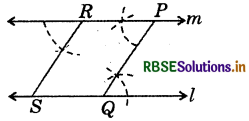
Step 1. Draw a line l and mark a point P outside it.
Step 2. Take a point Q on l and join PQ
Step 3. Draw m ∥ l through P.
Step 4. Mark a point R on m.
Step 5. Through R, draw RS ∥ PQ, such that it meets l at S.
Since, l ∥ m, so RP ∥ SQ also PQ ∥ RS. 
∴ PQSR is a parallelogram.