RBSE Solutions for Class 7 Maths Chapter 1 पूर्णांक Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 1 पूर्णांक Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 1 पूर्णांक Intext Questions

(प्रयास कीजिए पृष्ठ 2)

प्रश्न 1.
पूर्णांकों को निरूपित करने वाली एक संख्या रेखा नीचे दी गई है:

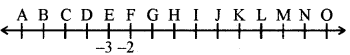
- 3 एवं - 2 को क्रमशः E और F से अंकित किया गया है। B, D, H, J, M एवं 0 द्वारा कौनसे पूर्णांक अंकित किए जाएंगे?
हल:
हम जानते हैं कि संख्या रेखा पर शून्य के दायीं ओर धन पूर्णांक तथा बायीं ओर ऋण पूर्णांक होते हैं।
चूँकि दी गई संख्या रेखा पर E तथा F पर - 3 तथा -2 दिया गया है। अतः इस संख्या रेखा पर E के -3 से बायीं ओर प्रत्येक इकाई पर ऋणात्मक 1 जोड़ते हुए निम्नानुसार - 4, - 5, - 6 तथा - 7 अंकित करेंगे। इसी प्रकार F के - 2 से दायीं ओर प्रत्येक इकाई पर धनात्मक 1 जोड़ते हुए निम्नानुसार - 1, 0, 1, 2, 3, 4, 5, 6 तथा 7 अंकित करेंगे।

इस प्रकार स्पष्ट है कि B, D, H, J, M एवं 0 द्वारा क्रमशः - 6, - 4, 0, 2, 5 एवं 7 पूर्णांक अंकित किए जाएंगे।

प्रश्न 2.
पूर्णांकों 7, -5, 4,0 एवं - 4 को आरोही क्रम में क्रमबद्ध कीजिए और अपने उत्तर की जाँच करने के लिए इन्हें एक संख्या रेखा पर अंकित कीजिए।
हल:
पूर्णांकों 7,-5, 4, 0 तथा - 4 का आरोही क्रम
- 5, - 4, 0, 4 और 7
इन संख्याओं को संख्या रेखा पर प्रदर्शित करने के लिए संख्या रेखा बनाई तथा इसके मध्य में एक बिन्दु 0 लिया। जैसा निम्न आकृति में दिया है। अब समान दूरी .. पर 0 के बायीं व दायीं ओर, 0 से आरम्भ करते हुए बिन्दु लिये और 0 से 4 इकाई दायीं ओर 4 प्राप्त किया और | उससे 3 इकाई दायीं ओर 7 प्राप्त किया।
फिर 0 से प्रारम्भ कर बायीं ओर 4 इकाई पर - 4 प्राप्त किया तथा वहाँ से 1 इकाई बायीं ओर - 5 प्राप्त किया।

इस प्रकार से प्राप्त पूर्णांक आरोही क्रम में हैं।

(प्रयास कीजिए पृष्ठ 4)

प्रश्न 1.
अपनी पिछली कक्षा में हमने संख्याओं के साथ विभिन्न प्रकार के प्रतिरूप (पैटर्न) ज्ञात किए हैं। क्या आप निम्नलिखित में से प्रत्येक के लिए एक पैटर्न ज्ञात कर सकते हैं? यदि हाँ, तो इनको पूरा कीजिए।
(a) 7, 3, - 1, - 5, ___, ___, ___ .
(b) - 2, - 4, - 6, - 8, ___, ___, ___ .
(c) 15, 10, 5, 0, ___, ___, ___ .
(d) - 11, - 8, - 5, - 2, ___ , ___ , ___ .
हल:
(a) स्पष्टतः, 7 - 4 = 3, 3 - 4 = -1 - 1 - 4 = -5
अतः उससे आगे की संख्याएँ -5, - 4 = -9. -9 - 4 = -13 तथा –13 – 4 = -17 होंगी।
इस प्रकार पैटर्न होगा: 7, 3, -1, -5, -9, -13, -17

(b) स्पष्टतः, इसमें हमें ज्ञात हैं -2 - 2 = -4, -4 - 2 = -6, -6 - 2 = -8।
अतः अगली संख्याएँ -8 - 2 = -10, -10 -2 = -12
तथा -12 - 2 = -14 होंगी। इस प्रकार पैटर्न होगा: -2, -4, -6, -8, -10, -12, -14

(c) स्पष्टतः, 15 - 5 = 10, 10 - 5 = 5, 5 - 5 = 0।
अतः अगली संख्याएँ 0 - 5 = -5, -5 - 5 = -10 और -10 - 5 = -15 होंगी।
इस प्रकार पैटर्न होगा : 15, 10, 5, 0, -5, -10, -15

(d) स्पष्टतः, -11 + 3 = -8, -8 + 3 = -5, -5 + 3 = -2
अतः अगली संख्याएँ -2 + 3 = 1, 1 + 3 = 4 और 4 + 3 = 7 होंगी।
इस प्रकार पैटर्न होगा : -11, -8, -5, -2, 1, 4, 7

(प्रयास कीजिए पृष्ठ 9)

प्रश्न 1.
एक ऐसा पूर्णांक युग्म लिखिए जिसके - योग से हमें निम्नलिखित प्राप्त होता है :
(a) एक ऋणात्मक पूर्णांक
(b) शून्य
(c) दोनों पूर्णांकों से छोटा एक पूर्णांक
(d) दोनों पूर्णांकों में से केवल किसी एक से छोटा पूर्णांक
(e) दोनों पूर्णांकों से बड़ा एक पूर्णांक।
हल:
(a) - 3 + (-4) = -3 - 4 = - 7 (एक ऋणात्मक पूर्णांक)
(b) - 10 + 10 = 0 (शून्य)
(c ) - 5 + (-3) = -5 - 3 = -8 (यह दोनों पूर्णांकों से छोटा है)
(d) 9 + (-4) = 9 - 4 = 5 (केवल 9 से छोटा पूर्णांक)
(e) 5 + 3 = 8 (दोनों पूर्णांकों से बड़ा पूर्णांक)

प्रश्न 2.
एक ऐसा पूर्णांक युग्म लिखिए जिसके अन्तर से हमें निम्नलिखित प्राप्त होता है :
(a) एक ऋणात्मक पूर्णांक
(b) शून्य
(c) दोनों पूर्णांकों से छोटा एक पूर्णांक
(d) दोनों पूर्णांकों में से केवल किसी एक से बड़ा पूर्णांक
(e) दोनों पूर्णांकों से बड़ा एक पूर्णांक
हल:
(a) - 8 तथा 5
(- 8) - (5) = - 8 - 5 = - 13 (एक ऋणात्मक पूर्णांक)

(b) 4 तथा 4
4 - 4 = 0 (शून्य)

(c) 9 तथा 7
9 - 7 = 2 (दोनों पूर्णांकों से छोटा एक पूर्णांक)

(d) 6 तथा 2
6 - 2 = 4 (दोनों पूर्णांकों में से केवल किसी एक से बड़ा पूर्णांक)

(e) 3 तथा - 7
3 - (-7) = 3 + 7 = 10 (दोनों पूर्णांकों से बड़ा एक पूर्णांक)

(प्रयास कीजिए पृष्ठ 10)

प्रश्न-संख्या रेखा का उपयोग करते हुए, ज्ञात कीजिए:
(i) 4 × (- 8)
(ii) 8 × (- 2)
(iii) 3 × (- 7)
(iv) 10 × (- 1)
हल:
(i) 4 × (- 8) = (- 8) + (- 8)+ ( -8) + (- 8)
इसको हम संख्या रेखा पर निम्न प्रकार से प्रदर्शित कर सकते हैं:

इसलिए, 4 × (- 8) = - 32

(ii) 8 × (- 2) = (- 2) + (- 2) + (- 2) + (- 2)
इसे हम निम्न प्रकार प्रदर्शित कर सकते हैं:

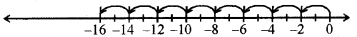
इसलिए, 8 × (- 2) = - 16

(iii) 3 × (- 7) = (- 7) + (- 7) + (- 7)
इसे हम संख्या रेखा पर निम्न प्रकार प्रदर्शित कर सकते हैं:

इसलिए, 3 × (- 7) = - 21

(iv) 10 × (- 1) = (- 1) + (- 1) + (- 1) + (- 1) + (- 1) + (- 1) + (- 1) + (- 1) + (- 1) + (- 1)
इसे हम संख्या रेखा पर निम्न प्रकार प्रदर्शित कर | सकते हैं :

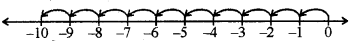
इसलिए, 10 × (- 1) = -10

(प्रयास कीजिए पृष्ठ 11)

प्रश्न-ज्ञात कीजिए:
(i) 6 × (- 19)
(ii) 12 × (-32)
(iii) 7 × (- 22)
हल:
(i) 6 × (- 19) = - (6 × 19) = - 114
(ii) 12 × (- 32) = - (12 × 32) = - 384
(iii) 7 × (- 22) = - (7 × 22) = - 154

(प्रयास कीजिए पृष्ठ 12)

प्रश्न 1.
ज्ञात कीजिए:
(a) 15 × (- 16)
(b) 21 × (- 32)
(c) (- 42) × 12
(d) - 55 × 15
हल:
(a) 15 × (-16) = - (15 × 16) = - 240
(b) 21 × (-32) = - (21 × 32) = - 672
(c) (- 42) × 12 = - (42 × 12) = - 504
(d) - 55 × 15 = - (55 × 15) = - 825

प्रश्न 2.
जाँच कीजिए कि क्या
(a) 25 × (- 21) = (- 25) × 21 है?
(b) (- 23) × 20 = 23 × (-20) है?
इस प्रकार के पाँच और उदाहरण लिखिए।
हल:
(a) बायाँ भाग = 25 × (-21)
= - (25 × 21) = - 525
दायाँ भाग = (- 25) × 21
= - (25 × 21) = - 525
अतः बायाँ भाग = दायाँ भाग।

(b) बायाँ भाग = (- 23) × 20
= - (23 × 20) = - 460
दायाँ भाग = 23 × (- 20)
= - (23 × 20) = - 460
अतः, बायाँ भाग = दायाँ भाग इस प्रकार के पाँच उदाहरण निम्न हैं:
(i) 25 × (-17) = (-25) × 17 = - (25 × 17)
(ii) 52 × (-24) = (-52) × 24 = - (52 × 24)
(iii) 9 × (-11) = (-9) × 11 = - (9 × 11)
(iv) 45 × (-22) = (-45) × 22 = – (45 × 22)
(v) 65 × (-26) = (-65) × 26 = - (65 × 26)

(प्रयास कीजिए पृष्ठ 13-I)

प्रश्न 1.
(i) (-5) × 4, से शुरू करते हुए, (-5) × (-6) ज्ञात कीजिए।
हल:
(- 5) × 4 = - 20
(- 5) × 3 = - 15 = - 20 + 5
(- 5) × 2 = - 10 = - 15 + 5
(- 5) × 1 = - 5 = - 10 + 5
(- 5) × 0 = 0 = - 5 + 5
(- 5) - (- 1) = 5 = 0 + 5
(- 5) × (- 2) = 10 = 5 + 5
(- 5) × (- 3) = 15 = 10 + 5
(- 5) × (- 4) = 20 = 15 + 5
(- 5) × (- 5) = 25 = 20 + 5
(- 5) × (- 6) = 30 = 25 + 5

(ii) (- 6) × 3 से शुरू करते हुए, (- 6) × (- 7) ज्ञात कीजिए।
हल:
(- 6) × 3 = -18
(- 6) × 2 = - 12 = - 18 + 6
(- 6) × 1 = - 6 = - 12 + 6
(- 6) × 0 = 0 = - 6 + 6.
(- 6) × (- 1) = 6 = 0 + 6
(- 6) × (- 2) = 12 = 6 + 6
(- 6) × (- 3) = 18 = 12 + 6
(- 6) × (- 4) = 24 = 18 + 6
(- 6) × (- 5) = 30 = 24 + 6
(- 6) × (6) = 36 = 30 + 6
(- 6) × (- 7) = 42 = 36 + 6

(प्रयास कीजिए पृष्ठ 13-II)

प्रश्न 1.
ज्ञात कीजिए: (-31) × (-100), (- 25) × (- 72), (- 83) × (- 28)
हल:
(i) (- 31) × (- 100) = 31 × 100 = 3100

(ii) (-25) × (-72)
= 25 × 72
= 1800

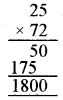
(iii) (- 83) × (- 28)
= 83 × 28
= 2324

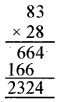
(सोचिए, चर्चा कीजिए एवं लिखिए पृष्ठ 15-16)

प्रश्न (i)
गुणनफल (-9) × (-5) × (- 6) × 1(- 3) धनात्मक है, जबकि गुणनफल (- 9) × (- 5) × 16 × (-3) ऋणात्मक है। क्यों?
हल:
(- 9) × (- 5) × (- 6) × (- 3) में ऋणात्मक पूर्णांकों की संख्या सम है। अतः इनका गुणनफल धन संख्या (पूर्णांक) होगा तथा (- 9) × (- 5) × 6 × (-3) में ऋणात्मक पूर्णांक विषम संख्या में है। अतः इनका गुणनफल ऋणात्मक पूर्णांक होगा।

प्रश्न (ii) गुणनफल का चिह्न क्या होगा, यदि हम निम्नलिखित को एक साथ गुणा करते हैं?
(a) आठ ऋणात्मक पूर्णांक एवं तीन धनात्मक पूर्णांक
(b) पाँच ऋणात्मक पूर्णांक और चार धनात्मक पूर्णांक
(c) (-1) को बारह बार
(d) (-1) को 2m बार, जहाँ m एक प्राकृत संख्या
हल:
(a) क्योंकि 8 एक सम संख्या है। अतः 8 ऋणात्मक पूर्णांक तथा 3 धनात्मक पूर्णांक का गुणनफल धनात्मक राशि ही होगी।
(b) क्योंकि 5 एक विषम संख्या है। अतः 5 ऋणात्मक तथा 4 धनात्मक पूर्णांकों का गुणनफल ऋणात्मक होगा।
(c) क्योंकि 12 सम संख्या है। अतः (-1) का 12 बार गुणनफल धनात्मक होगा।
(d) क्योंकि 2m राशि सम संख्या है। अतः (-1) 2m बार गुणा करने पर गुणनफल धनात्मक प्राप्त होगा।

(प्रयास कीजिए पृष्ठ 19-I)

प्रश्न 1.
(i) क्या 10 × [(6) + (-2)] = 10 × 6 + 10 × (-2) है?
हल:
हमें ज्ञात है:
10 × [(6) + (-2)] = 10 × [6 - 2] = 10 × 4 = 40
तथा 10 × 6 + 10 × (-2) = 60 - 20 = 40
∴ 10 × [(6) + (-2)] = 10 × 6 + 10 × (- 2)

(ii) क्या (-15) × [(-7) + (-1)] = (-15) × (-7) + (-15) × (-1) है?
हल:
हमें ज्ञात है:
(- 15) × [(- 7) + (- 1)] = (- 15) × (- 8) = 120
तथा (- 15) × (- 7) + (- 15) × (- 1) = 105 + 15 = 120
∴ (-15) × [(-7) + (-1)] = (-15) × (-7) + (-15) × (-1)

(प्रयास कीजिए पृष्ठ 19-II)

प्रश्न 1.
(i) क्या 10 × 6 - (-2)] = 10 × 6 - 10 × (-2) है?
हल:
(i) हमें ज्ञात है:
10 × [6 - (-2)1 = 10 × [6+2] = 10 × 8 = 80
तथा 10 × 6 - 10 × (-2) = 60 - (- 20) = 60 + 20 = 80
अतः 10 - [6 - (- 2)] = 10 × 6 - 10 - (-2)

(ii) क्या (-15) × [(-7) - (-1)] = (-15) × (-7) - (-15) × (-1) है?
हल:
हमें ज्ञात है:
(- 15) × [(- 7) - (-1)] = (- 15) × (- 7 + 1)
= (-15) × (-6) = 90 और - 15 × (-7) - (-15) × (- 1)
= 105 - 15 = 90 अतः (-15) × [(-7) - (- 1)]
= (-15) × (-7) - (-15) × (- 1)

(प्रयास कीजिए पृष्ठ 20)

प्रश्न वितरण गुण का उपयोग करते हुए (-49) × 18; (-25) ४ (-31); 70 × (-19) + (-1) × 70 के मान ज्ञात कीजिए।
हल:
(-49) × 18
= (- 49) × (20 - 2)
= (- 49) × 20 - (-49) × 2
= - 980 + 98 = - 882

(-25) × (-31)
= (-25) × [(-30) + (-1)]
= (-25) × (-30) + (-25) × (-1)
= 750 + 25 = 775

70 × (-19) + (-1) × 70
= 70 × (-19) + 70 × (-1)
= 70 × [(-19) + (-1)]
= 70 × (-20) = - 1400

(प्रयास कीजिए पृष्ठ 23)

प्रश्न 1.
ज्ञात कीजिए:
(a) (-100) ÷ 5
(b) (-81) ÷ 9
(c) (-75) ÷ 5
(d) (-32) ÷ 2
हल:
(a) (-100) ÷ 5 = -20
(b) (-81) 9 ÷ - 9 .
(c) (-75) ÷ 5 = -15
(d) (-32) ÷ 2 = -16

(प्रयास कीजिए पृष्ठ 24-I)

प्रश्न ज्ञात कीजिए:
(a) 125 ÷ (-25)
(b) 80 ÷ (-5)
(c) 64 ÷ (-16)
हल:
(a) 125 ÷ (-25) = - 5
(b) 80 ÷ (-5) = - 16
(c) 64 ÷ (-16) = - 4

(प्रयास कीजिए पृष्ठ 24-II)

प्रश्न ज्ञात कीजिए:
(a) (- 36) ÷ (- 4)
(b) (- 201) ÷ (- 3)
(c) (- 325) ÷ (- 13)
हल:
(a) (- 36) ÷ (- 4)
= 36 ÷ 4
= 9

(b) (- 201) ÷ (-3)
= 201 ÷ 3
= 67

(c) (- 325) ÷ (-13)
= 325 ÷ 13.
= 25

(प्रयास कीजिए पृष्ठ 25)

प्रश्न 1.
क्या किसी भी पूर्णांक a के लिए
(i) 1 ÷ a = 1 है?
(ii) a ÷ (- 1) = - a है?
a के विभिन्न मानों के लिए इनकी जाँच कीजिए।
हल:
(i) माना a = 4
∴ 1 ÷ a = 1 ÷ 4 = \(\frac{1}{4}\) ≠ 1
अतः 1 ÷ a = 1 असत्य है।

(ii) माना a = 8
∴ a ÷ (- 1) = 8 ÷ (-1) = - 8
अत: a ÷ (- 1) = - a सत्य है।