RBSE Solutions for Class 11 Maths Chapter 9 अनुक्रम तथा श्रेणी विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 9 अनुक्रम तथा श्रेणी विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 9 अनुक्रम तथा श्रेणी विविध प्रश्नावली

प्रश्न 1.
दर्शाइए कि किसी समान्तर श्रेढी के (m + n )वें तथा (m - n)वें पदों का योग mवें पद का दुगुना है।
हल:
माना कि किसी समान्तर श्रेढी का प्रथम पद a तथा सार्वअन्तर d है । हमें सिद्ध करना है कि
T_m+n + T_m-n = 2T_m
L.H.S. = T_m+n + T_m-n
= [a + (m + n - 1) d] + [a + (m - n - 1) d]
= 2a + (m + n - 1 + m - n - 1) d
= 2a + (2m - 2) d
= 2 [a + (m - 1) d]
= 2 T_m
= R.H.S.

प्रश्न 2.
यदि किसी समान्तर श्रेढी की तीन संख्याओं का योग 24 है तथा उनका गुणनफल 440 है, तो संख्याएँ ज्ञात कीजिए ।
हल:
माना कि तीन संख्याएँ a - d, a तथा a + d समान्तर श्रेढी में हैं
अतः इनका योग
⇒ प्रश्नानुसार a - d + a + a + d = 24
⇒ 3a = 24
⇒ a = 8
तथा इनका गुणनफल
= (a − d) (a) (a + d) = 440
या a (d² - d²) = 440
या 8 (64 – d²) = 440 [∵ a = 8]
या 64 - d² = \(\frac{440}{8}\) = 55
या d² = 64 - 55 = 9
∴ d² = ± 3
अतः वे संख्याएँ 8 - 3, 8, 8 + 3 या 8 + 3, 8, 8 - 3 या 5, 8, 11 या 11, 8, 5 होंगी।

प्रश्न 3.
माना कि किसी समान्तर श्रेढी के n, 2n तथा 3n पदों का योगफल क्रमशः S₁, S₂ तथा S₃ है तो दिखाइए कि S₃ = 3(S₂ - S₁)
हल:
माना कि किसी समान्तर श्रेढी का प्रथम पद a तथा सार्वअन्तर d है अत:

 

प्रश्न 4.
200 तथा 400 के मध्य आने वाली उन सभी संख्याओं का योगफल ज्ञात कीजिए जो 7 से विभाजित हों ।
हल:
200 से 400 के मध्य आने वाली 7 से विभाज्य हों क्रमश: 203, 210, 217, 224, 399 होंगी।
यहाँ a = 203, d = 210 - 203 = 7, l = T_n = 399
∴ T_n = a + (n - 1)d
या 399 = 203 + (n - 1)7
या 399 - 203 = (n - 1)7
या 196 = (n - 1)7
या (n - 1) = \(\frac{196}{7}\) = 28
अर्थात् 200 से 400 के मध्य 29 संख्याएँ होंगी ।
S_n = \(\frac{n}{2}\)(a+l)
= \(\frac{29}{2}\)(203+399)
= \(\frac{29}{2}\) × 602 = 29 × 301
= 8729

प्रश्न 5.
1 से 100 तक आने वाले उन सभी पूर्णांकों का योगफल ज्ञात कीजिए जो 2 या 5 से विभाजित हों ।
हल:
1 से 100 के मध्य 2 से भाज्य संख्याएँ 2, 4, 6, ............ 100
यहाँ दिया गया है a = 2, d = 2 एवं 1 = 100
∴ T_n = l = a + (n - 1)d
100 = 2 + (n - 1) × 2 = 2n
n = \(\frac{100}{2}\) = 50
अतः 2 + 4 + 6 + .......... + 100 तक की संख्याओं का योग
S_n = \(\frac{n}{2}\)[2a + (n - 1)d]
S_n = \(\frac{50}{2}\)[2 × 2 + (50 - 1) × 2]
= 25 [4 + 98]
= 25 × 102 = 2550
1 से 100 के मध्य 5 से भाज्य संख्यायें परन्तु 2 से भाज्य नहीं हो ।
5, 15, 25, ........... 95
यहाँ पर a = 5, d = 10, l = 95
∴ T_n = l = a + (n - 1) d
95 = 5 + (n - 1) × 10
⇒ 95 = 10n - 5
⇒ 10n = 100 ⇒ n = 10
S_n = \(\frac{n}{2}\)[2a + (n - 1)d]
⇒ S₁₀ = \(\frac{n}{2}\)[2a + (n - 1)d]
⇒ S₁₀ = \(\frac{10}{2}\)[2 × 5 + (10 - 1) × 10]
= 5 [10 + 90] = 5 × 100 = 500
अतः 2 या 5 से भाज्य संख्याओं का योग
= 2550 + 500 = 3050

प्रश्न 6.
दो अंकों की उन सभी संख्याओं का योगफल ज्ञात कीजिए, जिनको 4 से विभाजित करने पर शेषफल 1 हो।
हल:
दो अंकों की ऐसी संख्याएँ जो 4 से विभाजित हो जाएँ तथा शेषफल 1 बचे क्रमश: 13, 17, 21, ......... 97 होंगी।
a = 13, d = 17 – 13 = 4 तथा T_n = 97
⇒ 13 + (n - 1)4 = 97
⇒ 4(n - 1) = 84
या n - 1 = 21
n = 22
S₂₂ = \(\frac{n}{2}\)[a + l]
= \(\frac{22}{2}\)(13 + 97)
= 11 × 110 = 1210

प्रश्न 7.
सभी x, y ∈ N के लिए f (x + y) = f (x),f (y) को संतुष्ट करता हुआ एक ऐसा फलन है कि f(1) = 3 एवं \(\sum_{x=1}^n\) f(x) = 120 तो n का मान ज्ञात कीजिए ।
हल:
दिया है -f (x + y) = f (x) . f (y) ∀ x, y ∈ N
f(1) = 3
तथा \(\sum_{x=1}^n\)f(x) = 120
अब x = 1 तथा y = 1 के लिए
f(1 + 1) = f(1) . f(1)
f(2) = 3 × 3 = 9
x = 1 तथा y = 2 के लिए
f (1 + 2) = f (1) . f (2)
f(3) = 3 × 9 = 27

x = 1 तथा y = 3 के लिए
f (1 + 3) = f (1) . f (3)
f(4) = 3 × 27 = 81

अब L.H.S. = \(\sum_{x=1}^n\)f(x)
= f (1) + f (2) + f(3) + ............... + f (n)
= 3 + 9 + 27 + 81 + ..... n पदों तक
= \(\frac{3\left(3^n-1\right)}{3-1}=\frac{3}{2}\)(3n - 1)

अब \(\sum_{x=1}^n\)f(x) = 120
∴ \(\frac{3}{2}\)(3ⁿ - 1) = 120
⇒ (3ⁿ - 1) = 120
⇒ 3ⁿ - 1 = 80
⇒ 3ⁿ = 81 = 3⁴
n = 4

प्रश्न 8.
गुणोत्तर श्रेढी के कुछ पदों का योग 315 है, उसका प्रथम पद तथा सार्वअनुपात क्रमशः 5 तथा 2 हैं । अन्तिम पद तथा पदों की संख्या ज्ञात कीजिए ।
हल:
प्रश्नानुसार S_n = 315, a = 5 तथा r = 2

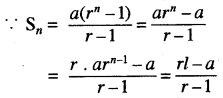
[∵ अंतिम पद l = a. r^n-1]
या 315 = \(\frac{2 l-5}{2-1}\)
यां 315 = 2l - 5
या 2l = 315 + 5 = 320
या l = \(\frac{320}{2}\) = 160
अब l = T_n = a .r^n-1
⇒ 160 = 5 (2)^n-1
या 2^n-1 = \(\frac{160}{5}\) = 32
या 2^n-1 = (2)⁵
या n - 1 = 5
n = 6

प्रश्न 9.
किसी गुणोत्तर श्रेढ़ी का प्रथम पद 1 है। तीसरे एवं पाँचवें पदों का योग 90 हो तो गुणोत्तर श्रेढ़ी का सार्वअनुपात ज्ञात कीजिए ।
हल:
प्रश्नानुसार किसी गुणोत्तर श्रेढ़ी का प्रथम पद 1 है। माना कि इसका सार्वअनुपात r है। अत:
T₃ + T₅ = 90 (दिया है)
a. r^3-1 + a.r^5-1 = 90
या 1.r^3-1 + 1.r^5-1 = 90 [∵ a = 1]
या r⁴ + r² = 90
या r⁴ + r² - 90 = 0
r² = y रखने पर y² + y - 90 = 0
या y² + 10y - 9y - 90 = 0
या y(y + 10) - 9(y + 10) = 0
या (y + 10)(y - 9) = 0
y = -10 या 9
y = - 10 की उपेक्षा करने पर y = 9
या r²
r = ± 3

प्रश्न 10.
किसी गुणोत्तर श्रेढ़ी के तीन पदों का योग 56 है। यदि हम क्रम से इन संख्याओं में से 1, 7, 21 घटाएँ तो हमें एक समान्तर श्रेढ़ी प्राप्त होती है । संख्याएँ ज्ञात कीजिए।
हल:
माना कि गुणोत्तर श्रेढ़ी के तीन पद a, ar तथा ar² हैं । अतः इनका योग
= a + ar + ar² = 56 ....(i)
इन पदों में से क्रमश: 1, 7 व 21 घंटाने पर नए पद क्रमशः a - 1, ar – 7 तथा ar² - 21 होंगे जो कि समान्तर श्रेढी में हैं ।
अर्थात् 2(ar - 7) = (a - 1) + (ar² - 21)
या 2ar - 14 = a - 1 + ar² - 21
या ar² - 2ar + a = 8

समीकरण (i) में से (ii) को घटाने पर
3ar = 48
या ar = \(\frac{48}{3}\) = 16
या a = \(\frac{16}{r}\) ............(iii)
समीकरण (i) में a = \(\frac{16}{r}\) रखने पर
या \(\frac{16}{r}\) + 16 + 16r = 56
या 16 + 16r+ 16r² = 56r
या 2r² - 5r + 2 = 0
या 2r² - 4r - r + 2 = 0
या 2r(r - 2) - 1(r - 2) = 0
या (r - 2)(2r - 1) = 0
r = 2 या \(\frac{1}{2}\)
यदि r = 2 तो a = \(\frac{16}{2}\) = 8
तब संख्याएँ क्रमश: 8, 16, 32 होंगी ।
यदि r = \(\frac{1}{2}\) तो a = \(\frac{16}{1 / 2}\) = 32
तब संख्याएँ क्रमशः 32, 16, 8 होंगी।

प्रश्न 11.
किसी गुणोत्तर श्रेढी के पदों की संख्या सम है । यदि उसके सभी पदों का योगफल, विषम स्थान पर रखे पदों के योगफल का 5 गुना है, तो सार्वअनुपात ज्ञात कीजिए ।
हल:
माना गुणोत्तर श्रेढी का प्रथम पद a, सार्वअनुपात r तथा पदों की संख्या 2n है । अतः श्रेढी a, ar, ar², ar³, ............ ar^2n-1 होगी ।
तब S_2n = \(\frac{a\left(r^{2 n}-1\right)}{r-1}\) जहाँ r > 1 ..........(i)
अब विषम स्थानों पर रखे पदों की संख्या = n
तथा इनका सार्वअनुपात = r²
विषम स्थानों पर रखे पदों से बनी श्रेणी a, ar², ar⁴, .............. होगी

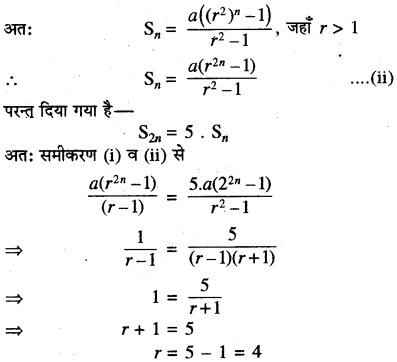
अतः दी गई श्रेढी का अभीष्ट सार्वअनुपात = 4

प्रश्न 12.
एक समान्तर श्रेढी के प्रथम चार पदों का योगफल 56 है। अन्तिम चार पदों का योगफल 112 है। यदि इसका प्रथम पद 11 है, तो पदों की संख्या ज्ञात कीजिए ।
हल:
माना कि किसी समान्तर श्रेढी के चार पद क्रमश: a, a + d, a + 2d तथा a + 3d हैं ।
अतः प्रश्नानुसार
a + (a + d) + (a + 2d) + (a + 3d) = 56
या 4a + 6d = 56
या 2a + 3d = 28....(i)

अन्तिम चार पद T_n, T_n-1, T_n-2 तथा T_n-3 हैं। अतः
T_n + T_n-1 + T_n-2 + T_n-3 = 112
या [a + (n - 1) d] + [a + (n - 2)d] + [a + (n - 3)d]
या 4a + 4nd - 10d = 112
या 2a + 2nd - 5d = 56 .........(ii)

समीकरण (i) से
2a + 3d = 28

समीकरण (ii) में मान रखने पर
2 × 11 + 2nd - 5d = 56
2nd - 5d = 34 ....(iii)

समीकरण (i) में मान रखने पर
2 × 11 + 3d = 28
3d = 6
या d = 2
d का मान समीकरण (iii) में रखने पर
⇒ 2n × 2 - 5 × 2 = 34
⇒ 4n - 10 = 34
या 4n = 44
∴ n = 11
अर्थात् पदों की संख्या 11 है।

प्रश्न 13.
यदि \(\frac{a+b x}{a-b x}=\frac{b+c x}{b-c x}=\frac{c+d x}{c-d x}\) (x ≠ 0) हो, तो दिखाइए कि a, b, c तथा d गुणोत्तर
हल:
हम जानते हैं कि यदि \(\frac{a}{b}=\frac{c}{d}\)

⇒ a, b, c, d गुणोत्तर श्रेढी में हैं।

प्रश्न 14.
किसी गुणोत्तर श्रेढी में S, n पदों का योग, P उनका गुणनफल तथा R उनके व्युत्क्रमों का योग हो तो सिद्ध कीजिए कि P²Rⁿ = Sⁿ.
हल:
माना कि n पदों की एक गुणोत्तर श्रेढी a, ar, ar² ........... ar^n-1 है। तब

प्रश्न 15.
किसी समान्तर श्रेढी का pवाँ, वाँ, वाँ पद क्रमशः a, b, c हैं, तो सिद्ध कीजिए
(q - r) a + (r - p) b + (p - q) c = 0
हल:
माना कि समान्तर श्रेढी का प्रथम पद A तथा सार्वअन्तर d है। तब
प्रश्नानुसार
T_p = a, T_q = b तथा T_c = c

या A + (p - 1) d = a ....(i)
A + (q - 1)d = b ......(ii)
A + (r - 1) d = c ....(iii)

अब समीकरण (ii) में से (iii), (iii) में से (i) तथा (i) में से (ii) को घटाने पर
(q - r) d = b - c ....(iv)
(r - p) d = c - a ...(v)
(p - 9) d = a - b ....(vi)

अब समीकरण (iv) को a से, (v) को b से तथा (vi) को c से गुणा करने पर
a (q - r) d = ab - ac
b (r - p) d = bc - ba
c (p - q)d = ca - bc

अब इन तीनों को जोड़ने पर
a(q - r)d + b(r - p) d + c(p - q)d = 0
अतः a (q - r) + (r - p) b + (p - q) c = 0

प्रश्न 16.
यदि a\(\left(\frac{1}{b}+\frac{1}{c}\right)\), b\(\left(\frac{1}{c}+\frac{1}{a}\right)\), c\(\left(\frac{1}{a}+\frac{1}{b}\right)\) समान्तर श्रेढी में हैं, तो सिद्ध कीजिए कि a, b, c समान्तर श्रेढी में हैं ।
हल:
प्रश्नानुसार a\(\left(\frac{1}{b}+\frac{1}{c}\right)\), b\(\left(\frac{1}{c}+\frac{1}{a}\right)\) तथा c\(\left(\frac{1}{a}+\frac{1}{b}\right)\) समान्तर
श्रेढी में हैं ।
सभी पदों में 1 जोड़ने पर

प्रत्येक पद में ab + bc + ca से भाग देने पर
⇒ \(\frac{1}{b c}, \frac{1}{c a}, \frac{1}{a b}\) भी समान्तर श्रेढी में हैं ।
प्रत्येक पद को abc से गुणा करने पर
⇒ \(\frac{a b c}{b c}, \frac{a b c}{c a}, \frac{a b c}{a b}\) समान्तर श्रेढी में हैं ।
⇒ a, b, c समान्तर श्रेढी में हैं ।

प्रश्न 17.
यदि a, b, c, d गुणोत्तर श्रेढी में हैं, तो सिद्ध कीजिए कि (aⁿ + bⁿ), (bⁿ + cⁿ), (cⁿ + dⁿ) गुणोत्तर श्रेढी में हैं।
हल:
प्रश्नानुसार a, b, c व d गुणोत्तर श्रेढी में हैं अर्थात्
\(\frac{d}{c}=\frac{c}{b}=\frac{b}{a}\) = r (माना कि)
⇒ b = ar, c = br = ar², d = cr = ar³
सिद्ध करना है कि aⁿ + bⁿ, bⁿ + cⁿ, cⁿ + dⁿ गुणोत्तर श्रेढी में हैं।
अर्थात् (bⁿ + cⁿ)² = (aⁿ + bⁿ)(cⁿ + dⁿ)
∴ जब a, b तथा C G. P. में होते हैं तब b² = ac
L.H.S. = (bⁿ + cⁿ)²
= [(ar)ⁿ + (ar²)ⁿ]²
= [(aⁿrⁿ + aⁿ. rⁿ)²
= [aⁿrⁿ. (1 + rⁿ)]²
= a²ⁿ, r²ⁿ (1 + rⁿ)² ............(i)

R.H.S. = (aⁿ + bⁿ) (cⁿ + dⁿ)
= [aⁿ + (ar)ⁿ] [(ar²)ⁿ + (ar³)ⁿ]
= aⁿ (1 + rⁿ) [aⁿ r²ⁿ + aⁿ r³ⁿ]
= aⁿ (1 + rⁿ) × aⁿ, r²ⁿ (1 + rⁿ)²
= a²ⁿ r²ⁿ (1 + r²)² ............(ii)
इसलिए समीकरण (i) तथा (ii) से
L.H.S. = R.H.S.

प्रश्न 18.
यदि x² - 3x + p = 0 के मूल a तथा b हैं तथा x² - 12x + q = 0 के मूल c तथा d हैं, जहाँ a, b, c, d गुणोत्तर श्रेढी के रूप में हैं। सिद्ध कीजिए कि (q + p) : (q - p) = 17 : 15
हल:
समीकरण x² - 3x + p = 0 के मूल a तथा b हैं अत:
a + b = 3 तथा ab = p .........(i)
पुन: समीकरण x² - 12x + q = 0 के मूल c तथा d हैं अतः
c + d = 12 तथा cd = q ..........(ii)
\(\frac{d}{c}=\frac{c}{b}=\frac{b}{a}\) = r
b = ar, c = br = ar² तथा d = cr = ar³
ये मान समीकरण (i) व (ii) में रखने पर

प्रश्न 19.
दो धनात्मक संख्याओं a तथा 6 के बीच समान्तर माध्य तथा गुणोत्तर माध्य का अनुपात m : n है। दर्शाइए कि
a: b = (m. (m + \(\sqrt{m^2-n^2}\)) : (m - \(\sqrt{m^2-n^2}\))
हल:
प्रश्नानुसार a तथा b के बीच समान्तर माध्य (AM) = \(\frac{a+b}{2}\)
तथा a और b के बीच गुणोत्तर माध्य (GM) = \(\sqrt{ab}\)
इन दोनों माध्यों का अनुपात = m: n

प्रश्न 20.
यदि a, b, c समान्तर श्रेढी में हैं, b, c, d गुणोत्तर श्रेढी में हैं तथा \(\frac{1}{c}, \frac{1}{d}, \frac{1}{e}\) समान्तर श्रेढी में हैं, तो सिद्ध कीजिए कि a, c, e गुणोत्तर श्रेढी में हैं ।
हल:
प्रश्नानुसार a, b तथा c समान्तर श्रेढी में हैं अर्थात्
b = \(\frac{a+c}{2}\) ......(i)
तथा b, c व d गुणोत्तर श्रेढी में हैं अर्थात्
c² = bd ......(ii)
तथा \(\frac{1}{c}, \frac{1}{d}\) व \(\frac{1}{e}\) समान्तर श्रेढी में हैं अर्थात्
\(\frac{2}{d}=\frac{1}{c}+\frac{1}{e}\)
या d = \(\frac{2 c e}{c+e}\) ........(iii)
समीकरण (ii) में समीकरण (i) तथा (iii) से b व d का मान रखने पर
c² = \(\frac{a+c}{2} \cdot \frac{2 c e}{c+e}\)
c² = \(\frac{c e(a+c)}{(c+e)}\)
या c ( c + e) = e (a + c)
या c² + ce = ae + ce
या c² = ae
अर्थात् a, c व e गुणोत्तर श्रेढी में हैं।

प्रश्न 21.
निम्नलिखित श्रेणियों के n पदों का योग ज्ञात कीजिए-
(i) 5+55 + 555 + .....
(ii) .6 + .66 + .666 + .....
हल:
(i) माना कि S_n = 5 + 55 + 555 + ..... n पदों तक
= 5 [1 + 11 + 111 + .............. n पदों तक ]

(ii) माना कि S_n = 6 + .66 + .666 + ...... n पदों तक
= 6 [.1 + .11 + .111 + .... n पदों तक]

प्रश्न 22.
श्रेढी का 20वाँ पद ज्ञात कीजिए- 2 × 4 + 4 × 6 + 6 × 8 + ...... + n पदों तक
हल:
दी गई श्रेढी = 2 × 4 + 4 × 6 + 6 × 8 + ...... + n पदों तक
T_n = [2, 4, 6, .......... n पदों तक].[4, 6, 8 ............ n पदों तक ]
= [2 + (n - 1)2]. [4 + (n - 1)2]
= [2 + 2n - 2]. [4 + 2n - 2]
= 2n (2n + 2)
= 4n (n + 1)
T₂₀ = 4 × 20 (20 + 1)
= 80 × 21 = 1680

प्रश्न 23.
श्रेढी 3 + 7 + 13 + 21 + 31 + ............ के पदों का योग ज्ञात कीजिए ।
हल:
माना
S_n = 3 + 7 + 13 + 21 +31 + ....... + T_n....(i)
एक स्थान आगे बढ़ाकर लिखने पर
S_n = 3 + 7 + 13 + 21 + .......... + T_n-1 + T_n .......(ii)
समीकरण (i) में से (ii) को घटाने पर
0 = 3 + [4 + 6 + 8 + 10 + ... (n - 1) पदों तक ] - T_n
T_n = 3 + \(\frac{n-1}{2}\) [2 x 4 + (n − 2). 2]
= 3 + \(\frac{n-1}{2}\)[8 + 2n - 4]
= 3 + \(\frac{n-1}{2}\)·(2n + 4)
T_n = 3 + (n - 1)(n + 2)
= 3 + n² + 2n - n - 2
= n² + n - 2 + 3
T_n = n² + n + 1
∵ दी हुई श्रेढी का योग S_n = ΣT_n = Σn² + Σn + Σ1

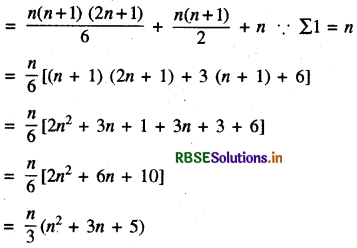
प्रश्न 24.
यदि S₁, S₂, S₃ क्रमश: प्रथम n प्राकृत संख्याओं का योग, उनके वर्गों का योग तथा घनों का योग है तो सिद्ध कीजिए कि
9S₂₂ = S₃ (1 + 8S₁).
हल:
प्रथम n प्राकृत संख्याओं का योग है अतः
S₁ = \(\frac{n(n+1)}{2}\)
प्रथम n प्राकृत संख्याओं के वर्गों का योग S₂ है अत:
S₂ = \(\frac{n(n+1)(2 n+1)}{6}\)
तथा प्रथम n प्राकृत संख्याओं के घनों का योग S₃ है अतः
S₃ = \(\left\{\frac{n(n+1)}{2}\right\}^2\)
अब प्रश्नानुसार R.H.S. = S₃ (1 + 8 S₁)

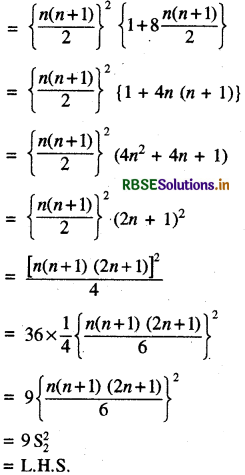
प्रश्न 25.
निम्नलिखित श्रेणियों के पदों तक योग ज्ञात कीजिए-
\(\frac{1^3}{1}+\frac{1^3+2^3}{1+3}+\frac{1^3+2^3+3^3}{1+3+5}\) + ..........
हल:

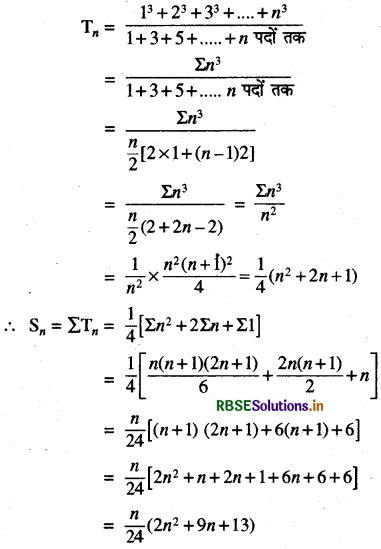
प्रश्न 26.
दर्शाइए कि \(\frac{1 \times 2^2+2 \times 3^2+\ldots .+n \times(n+1)^2}{1^2 \times 2+2^2 \times 3+\ldots .+n^2 \times(n+1)}=\frac{3 n+5}{3 n+1}\)
हल:
अंश के लिए - माना कि दी गई श्रेढी का nवाँ पद T_n है ।
T= [1, 2, 3 , ........... का n वाँ पद] [2, 3, 4.... का वाँ पद]²
[1 + (n - 1)1] [2 + (n - 1) 1]²
= n (n + 1)²
= n (n² + 2n + 1)
T_n = n³ + 2n² + n
S_n = Σn³ + 2Σn² + Σn

प्रश्न 27.
कोई किसान एक पुराने ट्रैक्टर को 12,000 रुपए में खरीदता है । वह 6,000 रुपए नकद भुगतान करता है और शेष राशि को 500 रुपए की वार्षिक किस्त के अतिरिक्त उस धन पर जिसका भुगतान न किया गया हो, 12% वार्षिक ब्याज भी देता है। किसान को ट्रैक्टर की कुल कितनी कीमत देनी पड़ेगी?
हल:
पुराने ट्रैक्टर का मूल्य = 12,000 रुपए
नकंद भुगतान = 6,000 रुपए
शेष राशि = 12,000 - 6,000
= 6, 000 रुपए
एक किस्त की राशि = 500
∴ कुल किस्तों की संख्या = \(\frac{6,000}{500}\) = 12
6,000 रुपए मूलधन पर 12% प्रतिवर्ष की दर से 1 वर्ष का ब्याज़
= \(\frac{6,000 \times 12 \times 1}{100}\) = 720 रुपए

एक वर्ष बाद राशि का भुगतान = 500 + 720 = 1,220 रुपए
दो वर्ष बाद ब्याज = \(\frac{5,500 \times 12 \times 1}{100}\)
= 660 रुपए
दो वर्ष बाद राशि का भुगतान = 500 + 660
= 1,160 रुपए
तीन वर्ष बाद ब्याज = \(\frac{5,000 \times 12 \times 1}{100}\)
= 600 रुपए
तीन वर्ष बाद राशि का भुगतान = 500 + 600
= 1,100 रुपए
इस प्रकार 1,220 + 1,160 + 1,100 + ........... 12 किस्तें

यहाँ a = 1,220 रुपए, d = - 60, n = 12
S₁₂ = \(\frac{12}{2}\)[2 × 1,220 + (12 - 1) (- 60)]
= 6 [2,440 - 660]
= 6 × 1,780 = 10,680 रुपए
अतः किसान द्वारा दी गई राशि
= 6,000 + 10,680
= 16,680 रुपए

प्रश्न 28.
शमशाद अली 22,000 रुपए में एक स्कूटर खरीदता है । वह 4,000 रुपए नकद देता है तथा शेष राशि को 1,000 रुपए वार्षिक किस्त के अतिरिक्त उस धन पर जिसका भुगतान न किया गया हो 10% वार्षिक ब्याज भी देता है। उसे स्कूटर के लिए कुल कितनी राशि चुकानी पड़ेगी ?
हल:
स्कूटर का मूल्य = 22,000 रुपए
नकद भुगतान = 4,000 रुपए
शेष = 22,000 - 4,000 = 18,000 रुपए
एक किस्त की राशि = 1,000 रुपए
कुल किस्तें: = \(\frac{18,000}{1,000}\) = 18,000 रुपए
18,000 रुपए पर 1 वर्ष का 10% प्रतिवर्ष की दर से ब्याज
= \(\frac{17,000 \times 10 \times 1}{100}\) = 1,700 रुपए
प्रथम किस्त = 1,000 + 1,800 = 2,800 रुपए
17,000 रुपए पर 1 वर्ष का 10% प्रतिवर्ष की दर से ब्याज
= \(\frac{17,000 \times 10 \times 1}{100}\) = 1, 700 रुपए
द्वितीय किस्त = 1,000 + 1,700 = 2,700 रुपए देय किस्तें
अतः 18 माह तक कुल = 2,800, 2,700, 2,600..... 18 पद
यहाँ a = 2,800 रुपए, d = -100, n = 18
S₁₈ = \(\frac{18}{2}\)[2 × 2,800 + (18 - 1).- 100]
= 9 [5,600 - 1,700]
= 9 × 3,900 = 35,100 रुपए
∴ शमशाद द्वारा स्कूटर की कुल चुकाई गई राशि
= 4,000 + 35,100 = 39,100 रुपए

प्रश्न 29.
एक व्यक्ति अपने चार मित्रों को पत्र लिखता है । वह प्रत्येक को उसकी नकल करके चार दूसरे व्यक्तियों को भेजने का निर्देश देता है, तथा उनसे यह भी करने को कहता है कि प्रत्येक पत्र प्राप्त करने वाला व्यक्ति इस श्रृंखला को जारी रखे। यह कल्पना करके कि श्रृंखला न टूटे तो 8वें पत्रों के समूह भेजे जाने तक कितना डाक खर्च होगा जबकि एक पत्र का डाक खर्च 50 पैसे है।
हल:
प्रथम व्यक्ति चार पत्र लिखता है । पुनः पत्र प्राप्त करने वाले चारों व्यक्ति चार-चार पत्र लिखते हैं। इस प्रकार श्रृंखला बढ़ती जाती है । इस प्रकार पत्रों की क्रमशः संख्याएँ
4, 16, 64, .......... 8 पदों तक
कुल पत्रों की संख्या = 4 + 16 + 64 + ...... 8 पदों तक यह एक गुणोत्तर श्रेणी है ।
S_n = \(\frac{a\left(r^n-1\right)}{r-1}\)
= \(\frac{4\left(4^8-1\right)}{4-1}=\frac{4}{3}\)(65,536 - 1)
= \(\frac{4}{3}\) × 65,535 = 87,380

एक पत्र का डाक खर्च = 50 पैसे = \(\frac{1}{2}\) रुपए
कुल डाक खर्च = 87,380 × \(\frac{1}{2}\)
= 43,690 रुपए

प्रश्न 30.
एक आदमी ने एक बैंक में 10,000 रुपए 5% वार्षिक साधारण ब्याज पर जमा किया। जब से रकम बैंक में जमा की गई तब से, 15वें वर्ष में उसके खाते में कितनी रकम हो गई तथा 20 वर्षों बाद कुल कितनी रकम हो गई, ज्ञात कीजिए ।
हल:
बैंक में जमा की गई राशि = 10,000 रुपए
ब्याज की दर = 5% वार्षिक साधारण ब्याज पर
एक वर्ष बाद ब्याज = \(\frac{10,000 \times 5 \times 1}{100}\) = 500 रुपए
अर्थात् उस व्यक्ति को प्रतिवर्ष 500 रुपए ब्याज मिलेगा। इस प्रकार उसके खाते में पहले, दूसरे, तीसरे, वर्ष क्रमशः 10,000, 10,500, 11,000, रुपए होंगे। अतः 15वें वर्ष में उसके खाते की राशि = ( 10,000 + 14 × 500) 17,000 रुपए

तथा 20 वर्ष के बाद उसके खाते की राशि अर्थात् 21वें वर्ष में राशि
T_n = a + (n - 1)d
T₂₁ = (10,000 + 20 × 500)
∵ a = 10,000, n = 21, d = 500
= 10,000 + 10,000
= 20,000 रुपए उत्तर

प्रश्न 31.
एक निर्माता घोषित करता है कि उसकी मशीन जिसका मूल्य 15,625 रुपए है, हर वर्ष 20% की दर से उसका अवमूल्यन होता है। 5 वर्ष बाद मशीन का अनुमानित मूल्य ज्ञात कीजिए ।
हल:
दिया गया है कि मशीन का वर्तमान मूल्य = 15,625 रुपए
अवमूल्यन की दर = 20% प्रति वर्ष
अतः 1 वर्ष पश्चात् मशीन का मूल्य
= 15,625 - 15,625 का 20%
= 15,625 - \(\frac{15,625 \times 20}{100}\)
= 15,625 - 3,125
= 12,500 रुपए
इसी तरह से 2 वर्ष पश्चात् मशीन का मूल्य
= 12,500 - \(\frac{12,500 \times 20}{100}\)
= 12,500 - 2,500
= 10,000 रुपए
3 वर्ष पश्चात् मशीन का मूल्य
= [10, 000 - \(\frac{10,000 \times 20}{100}\)]
= 10,000 - 2,000
= 8,000 रुपए
अतः मशीन के मूल्य को क्रमबद्ध करने पर, 12,500, 10,000, 8,000....
यह अनुक्रम गुणोत्तर श्रेढी है जिसका प्रथम पद
a = 12,500
तथा सार्वअनुपात r = \(\frac{10,000}{12,500}=\frac{4}{5}\)

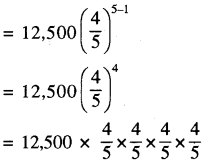
अतः 5 वर्ष पश्चात् मशीन का अभीष्ट मूल्य = 5,120 रुपए

प्रश्न 32.
किसी कार्य को कुछ दिनों में पूरा करने के लिए 150 कर्मचारी लगाए गए। दूसरे दिन 4 कर्मचारियों ने काम छोड़ दिया, तीसरे दिन 4 और कर्मचारियों ने काम छोड़ दिया तथा इस प्रकार अन्य । अब कार्य पूर्ण करने में 8 दिन अधिक लगते हैं, तो दिनों की संख्या ज्ञात कीजिए, जिनमें कार्य पूर्ण किया गया।
हल:
माना कि 150 कर्मचारी उस कार्य को n दिनों में पूरा करते हैं ।
अतः 150 कर्मचारियों का 1 दिन का काम = \(\frac{1}{n}\)
तथा 1 कर्मचारी का 1 दिन का काम = \(\frac{1}{150n}\)
पहले दिन 150 कर्मचारियों द्वारा 1 दिन में किया गया कार्य = \(\frac{150}{150 n}\)
दूसरे दिन 146 कर्मचारियों द्वारा 1 दिन में किया गया कार्य = \(\frac{146}{150 n}\)
तीसरे दिन 142 कर्मचारियों द्वारा 1 दिन में किया गया कार्य = \(\frac{142}{150 n}\)
कार्य पूर्ण होने में लगा कुल समय = n + 8 दिन
\(\frac{150}{150 n}+\frac{146}{150 n}+\frac{142}{150 n}\) + ... + (n + 8) पदों तक = 150 n
या \(\frac{1}{150 n}\)[150 + 146 + 142 + ...... + (n + 8) पदों तक] = 1
या \(\frac{(n+8)}{2}\)[2 × 150 + (n + 8 - 1) × (- 4)] = 150 n
या (n + 8) (- 4n + 272) = 300 n
या (n + 8) (n - 68) = - 75 n
या n² - 60n - 544 = -75n
या n² + 15n - 544 = 0
या (n + 32)(n - 17) = 0
या n = -32
या n = 17
क्योंकि n = -32 असम्भव है n = 17
∴ लगने वाला कुल समय = 17 + 8 = 25 दिन