RBSE Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.4
Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.4 Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 11 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 11. Students can also read RBSE Class 11 Maths Important Questions for exam preparation. Students can also go through RBSE Class 11 Maths Notes to understand and remember the concepts easily.
RBSE Class 11 Maths Solutions Chapter 9 Sequences and Series Ex 9.4
Find the sum to n terms of each of the series in exercise 1 to 7
Question 1.
1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + ...................
Answer:
Let the sum of n terms of series be Sn.
Sn = (1 × 2) + (2 × 3) + (3 × 4) + (4 × 5) + ......... + n terms
Now,nth term of given series
= [1, 2, 3, 4, ........ nth term] × nth term of [2, 3, 4, 5, ...............]
Tn = [1 + (n - 1).1] × [2 + (n - 1).1]
[∵ nth term of A.P. = a + (n - 1)d]
⇒ T n = n(n + 1)


Question 2.
1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 ..............
Answer:
Let the sum of n terms of the sequence is S.
Sn = 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + .............. n terms
nth term of series = nth term of [1, 2, 3, ..........] × nth term of [2, 3, 4, ..............] × n term of [3, 4, 5, ................]
Tn = [1 + (n - 1).1] × [2 + (n - 1).1] × [3 + (n - 1).1]
[∵ nth term of A.P. = 9 + (n - 1)d]
Tn = (1 + n - 1) (2 + n - 1) (3 + n - 1)
= n (n + 1) (n + 2)
= n(n2 + 3n + 2)
= n3 + 3n2 + 2n

∴ Sn = \(\frac{1}{4}\) n(n + 1) (n + 2) (n + 3)
Thus, sum of n terms of the given series
= \(\frac{1}{4}\) n(n + 1) (n + 2) (n + 3)
Question 3.
3 × 12 + 5 × 22 + 7 × 32 + .............
Answer:
Let sum of n terms of series be Sn.
Then Sn = 3 × 12 + 5 × 22 + 7 × 32 + .................. + n terms
nth term of series = (nth term of 3 + 5 + 7 + .... ) × n2
[∵ an = a + (n - 1)d]
= [3 + (n - 1) × 2]n2
= [3 + 2n - 2] × n2
= (2n + 1) n2
= 2n3 + n2


Question 4.
\(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}+\ldots \ldots\)
Answer:
Let the sum of n terms of series is Sn.


Question 5.
52 + 62 + 72 + .......... + 202
Answer:
Given series = 52 + 62 + 72 + ....................... + 202
So, nth term of series
= [nth term of sequence]
= [5 + (n - 1) × 1]2 (∵ 5, 6, 7, ... are in A.P.)
= [5 + n - 1]2
= (n + 4)2 = n2 + 8n + 16
Sum of n terms of series
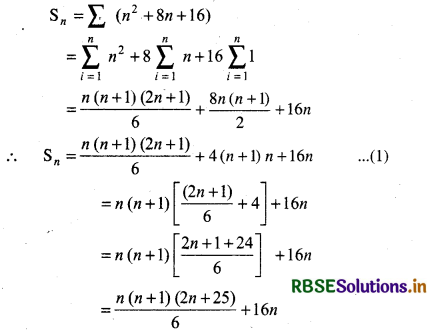
We see that last term of sequence 5, 6, 7, ........ 20 is 20.
Since, Tn = a + (n - 1)d
20 = 5 + (n - 1) × 1
⇒ 20 = 5 + n - 1
⇒ 20 = n + 4
⇒ n = 16
Putting n =16 in equation (1), we have
S16 = \(\frac{16(16+1)(2 \times 16+25)}{6}\) + 16 × 16
= \(\frac{16 \times 17 \times 57}{6}\) + 256
= 8 × 17 × 19 + 256
= 2584 + 256
= 2840
Thus, 52 + 62 + 72 + ...................... + 202 = 2840
Note: Since, series is 52 + 62 + 72 + ...................... + 202 and square of numbers are from 5 to 20. Thus, number of terms will be 16.

Question 6.
3× 8 + 6 × 11 + 9 × 14 + ...........
Answer:
Given series 3 × 8 + 6 × 11 + 9 × 14 + .............. n terms
Let nth term of sequence be Tn.
Tn = (nth term of sequence 3, 6, 9, ............ ) × (nth term of sequence 8, 11, 14 ............)
= [3 + (n - 1) × 3] × [8 + (n - 1) × 3]
[∵ nth term of A.p. = a + (n - 1)d]
= [3 + 3n - 3] × [8 + 3n - 3]
= 3n × (3n + 5)
= 9n2 + 15n
Let Sn be the sum of n term of the series.

= n(n + 1) (3n + 9)
= 3n (n + 1) (n + 3)
Thus, sum of n terms of the given series
Sn = 3n(n + 1) (n + 3)
Question 7.
12 + (12 + 22) + (12 + 22 + 32) + ..............
Answer:
Given series = 12 + (12 + 22) + (12 + 22 + 32) + .............. n terms
nth term of series = 12 + 22 + ............... + n2


Find the sum of n terms of the series ¡n exercIse 8 to 10 whose nth term is given by:
Question 8.
n(n + 1) (n + 4)
Answer:
nth term of the given series = n (n + 1) (n + 4)
Tn = n(n2 + 5n + 4)
Tn = n3 + 5n2 + 4n
Let Sn be the sum of n terms of the sequence.
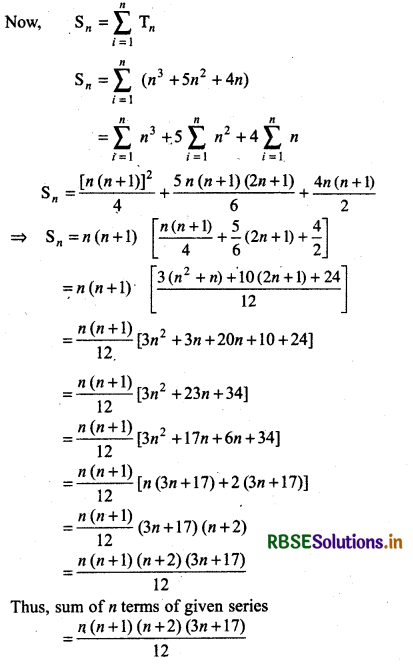
Question 9.
n2 + 2n
Answer:
nth term of the series Tn = n2 + 2n


Question 10.
(2n - 1)2
Answer:
nth term of given series Tn = (2n - 1)2
= 4n2 - 4n + 1
Let Sn be the sum of n terms of the sequence
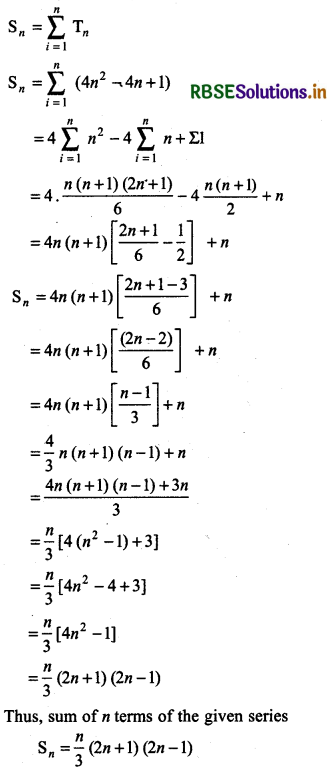

- RBSE Solutions for Class 11 Maths Chapter 3 त्रिकोणमितीय फलन Ex 3.1
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन विविध प्रश्नावली
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.3
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.2
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.1
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय विविध प्रश्नावली
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.6
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.5
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.4
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.3
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.2