RBSE Solutions for Class 11 Maths Chapter 9 अनुक्रम तथा श्रेणी Ex 9.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 9 अनुक्रम तथा श्रेणी Ex 9.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 10 सरल रेखाएँ Ex 9.2

प्रश्न 1.
1 से 2001 तक के विषम पूर्णांकों का योग ज्ञात कीजिए ।
हल:
प्रश्नानुसार S_n = 1 + 3 + 5 + 7 + ................ + 2001
यहाँ a = 1, d = 3 - 1 = 2, l = 2001
माना T_n = 2001
∵ T_n = a + (n - 1)d
⇒ 1 + (n - 1) (2) = 2001
⇒ 2(n - 1) = 2000
⇒ n - 1 = 1000
∴ n = 1001
∵ S_n = \(\frac{n}{2}\)[a + 1]
∴ S₁₀₀₁ = \(\frac{1001}{2}\)[1 + 2001]
= \(\frac{1001}{2}\) [2002] = 1001 × 1001
= 1002001

प्रश्न 2.
100 तथा 1000 के मध्य उन सभी प्राकृत संख्याओं का योगफल ज्ञात कीजिए जो 5 के गुणज हों ।
हल:
100 तथा 1000 के मध्य 5 के गुणज क्रमश: 105, 110, 115, .................... 995 होंगे।
∴ a = 105, d = 110 - 105 = 5, l = T_n = 995
∵ 995 = 105 + (n - 1) 5
∴ 995 - 105 = 5 (n - 1)

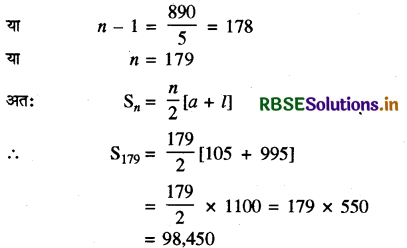
प्रश्न 3.
किसी समान्तर श्रेढी में प्रथम पद 2 है तथा प्रथम पाँच पदों का योगफल, अगले पाँच पदों के योगफल का एक-चौथाई है। दर्शाइए कि 20वाँ पद - 112 है।
हल:
माना कि किसी समान्तर श्रेणी का सार्वअन्तर d है तथा प्रश्नानुसार a = 2
∴ प्रथम पाँच पदों का योगफल = \(\frac{5}{2}\) [2 × 2 + 4 . d]
[∵ S_n = \(\frac{n}{2}\) [2a + (n - 1)d]
= 5 [2 + 2d] = 10 (1 + d)
छठा पद 2 + (6 − 1). d = 2 + 5d
अतः अगले पाँच पदों का योगफल
= \(\frac{5}{2}\) [2 (2 + 5d) + (5 - 1) d]
= \(\frac{5}{2}\) [4 + 10d + 4d]
= \(\frac{5}{2}\) [4 + 14d] = 5 (2 + 7d)
प्रश्नानुसार प्रथम पाँच पदों का योगफल = \(\frac{1}{4}\) अगले पाँच पदों का योगफल
⇒ 10 (1 + d) = \(\frac{1}{4}\) × 5 (2 + 7d)
⇒ 8 + 8d = 2 + 7d
⇒ d = 2 - 8 = - 6
∴ 20वाँ पद = T₂₀ = a + (n - 1)d
= 2 + (20 - 1) (- 6) = 2 + 19 × (- 6)
= 2 - 114 = - 112

प्रश्न 4.
समान्तर श्रेढी 6, - \(\frac{11}{2}\), - 5, ................. के कितने पदों का योगफल - 25 है?
हल:

⇒ - 100 = n (n = 25)
⇒ n² - 25n + 100 = 0
⇒ n² - 20n - 5n + 100 = 0
⇒ n (n - 20) - 5 (n - 20) = 0
⇒ (n - 20) (n - 5) = 0
∴ n = 5 य 20

प्रश्न 5.
किसी समान्तर श्रेढी का p वाँ पदों \(\frac{1}{q}\) का योगफल \(\frac{1}{p}\) हो तो सिद्ध कीजिए कि प्रथम pg पदों का योग \(\frac{1}{2}\)(pq + 1 ) होगा जहाँ p ≠ q.
हल:
माना कि किसी समान्तर श्रेढी का प्रथम पद a तथा सार्वअन्तर d है तथा हमें सिद्ध करना है कि

प्रश्न 6.
यदि किसी समान्तर श्रेढी 25, 22, 19, ................. योगफल 116 है तो अंतिम पद ज्ञात कीजिए ।
हल:
यहाँ a = 25, d = 22 - 25 = - 3
माना कि इस समान्तर श्रेढी में n पद हैं । अतः 1 पदों का योगफल
(S_n) = \(\frac{n}{2}\) [2a + (n - 1) d]
या 116 = \(\frac{n}{2}\) [2 × 25 + (n - 1) (- 3)]
या 232 = n[50 - 3n + 3]
या 232 = 50n - 3n² + 3n
या 3n² - 53n + 232 = 0
या 3n² - 29n - 24n + 232 = 0
या n(3n - 29) - 8 (3n - 29) = 0
या (3n - 29) (n - 8) = 0
∴ n = 8 क्योंकि n ≠ \(\frac{29}{3}\)
∴ आठवाँ पद T₈ = a + (n - 1)d
= 25 + (8 - 1), (- 3)
= 25 + 7 × (- 3)
= 25 - 21 = 4

प्रश्न 7.
उस समान्तर श्रेढी के n पदों का योगफल ज्ञात कीजिए, जिसका k वाँ पद 5k + 1 है।
हल:
∵ k वाँ पद T_k = 5k + 1
∴ T₁ = 5 . 1 + 1 = 5 + 1 = 6
T₂ = 5 . 2 + 1 = 10 + 1 = 11
T₃ = 5 . 3 + 1 = 15 + 1 = 16
T₄ = 5 . 4 + 1 = 20 + 1 = 21
अतः a = 6, d = 11 - 6 = 5
∴ S_n = \(\frac{n}{2}\) [2a + (n - 1)d]
= \(\frac{n}{2}\) [2 × 6 + (n - 1)5]
= \(\frac{n}{2}\) [12 + 5n - 5]
= \(\frac{n}{2}\) [5n + 7]

प्रश्न 8.
यदि किसी समान्तर श्रेढी के n पदों का योगफल (pn + qn)² है, जहाँ p तथा q अचर हों तो सार्वअन्तर ज्ञात कीजिए।
हल:
प्रश्नानुसार n पदों का योगफल (S_n) = pn + qn²
∴ S₁ = p × 1 + q(1)² = p + q = T₁
S₂ = p × 2 + q(2)² = 2p + 4q = T₁ + T₂
S₃ = p × 3 + q(3)² = 3p + 9q = T₁ + T₂ + T₃
T₂ = 2p + 4q - p - q = p + 3q
T₃ = 3p + 9q - (2p + 4q) = p + 5q
∴ d = T₂ - T₁ = p + 3q - p - q = 2q
d = T₃ - T₂ = p + 5q - p - 3q = 2q
अतः श्रेढी का सार्वअन्तर d = 2q है।

प्रश्न 9.
दो समान्तर श्रेढियों के n पदों के योगफल का अनुपात 5n + 4 : 9n + 6 हो, तो उनके 18 वें पदों का अनुपात ज्ञात कीजिए।
हल:
माना कि प्रथम समान्तर श्रेढी का प्रथम पद a₁, सार्वअन्तर d₁ तथा n पदों का योग S_n1 है तथा इसी प्रकार द्वितीय समान्तर श्रेढी का प्रथम पद a₂, सार्वअन्तर d₂ तथा n पदों का योग S_n2 है।
प्रश्नानुसार दिया है कि \(\frac{S_{n 1}}{S_{n 2}}\) = \(\frac{5 n+4}{9 n+6}\)

प्रश्न 10.
यदि किसी समान्तर श्रेढी के प्रथम p पदों का योग, प्रथम q पदों के योगफल के बराबर हो तो प्रथम (p + q) पदों का फलज्ञात कीजिए।
हल:
माना कि समान्तर श्रेढी का प्रथम पद a तथा सार्वअन्तर d है।
अतः
प्रथम p पदों का योगफल = \(\frac{p}{2}\)[2a + (p - 1)d] ........ (i)
तथा प्रथम q पदों का योगफल = \(\frac{q}{2}\) [2a + (q - 1)d] ............ (ii)
प्रश्नानुसार p पदों का योगफल = q पदों का योगफल
अर्थात् \(\frac{p}{2}\)[2a + (p - 1)d] = \(\frac{q}{2}\)[2a + (q - 1)d]
2ap + p (p - 1)d = 2aq + q (q - 1)d
या 2a (p - q) + [p (p - 1) - q (q - 1)] d = 0
या 2a (p - q) + (p² - q²) - (p - q)]d = 0
या 2a (p - q) + (p - q) (p + q - 1)]d = 0
p - q से भाग देने पर 2a + (p + q - 1) d = 0 .... (iii)
अब (p + q) पदों का योगफल = \(\frac{p+q}{2}\) [2a + (p + q - 1)d]
[∵ S_n = \(\frac{n}{2}\) [2a + (n - 1)d]]
= \(\frac{p+q}{2}\) × 0 [समीकरण (iii) से मान रखने पर]
= 0

प्रश्न 11.
यदि किसी समान्तर श्रेढी के प्रथम p q r पदों का योगफल क्रमशः a, b तथा c हो तो सिद्ध कीजिए कि \(\frac{a}{p}\) (q - r) + \(\frac{b}{q}\) (r - p) + \(\frac{c}{r}\) (p - q) = 0
हल:
माना कि समान्तर श्रेढी का प्रथम पद A तथा सार्वअन्तर D है,

प्रश्न 12.
किसी समान्तर श्रेढी के m तथा n पदों के योगफलों का तो दशाइए कि m वें तथा n वें पदों का अनुपात m² : n² है अनुपात (2m - 1 ) : (2n - 1) है।
हल:
माना समान्तर श्रेढी का प्रथम पद a एवं सार्वअन्तर d है।

समीकरण (i) एवं (ii) में d के गुणांकों को समान बनाने के लिए समीकरण (i) m के स्थान पर (2m - 1) एवं n के स्थान पर (2n - 1) रखने पर,

प्रश्न 13.
यदि किसी समान्तर श्रेढी के n वें पद का योगफल 3n² + 5n है तथा इसका m वाँ पद 164 है, तो m का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार S_n = 3n² + 5n
∴ S₁ = 3(1)² + 5(1) = 3 + 5 = 8 ⇒ T₁ = 8
S₂ = 3(1)² + 5(2)
= 12 + 10 = 22
∴ T₁ + T₂ = 22
या 8 + T₂ = 22
∴ T₂ = 22 - 8 = 14
अब a = 8, d = 14 - 8 = 6 तथा T_m = 164
∴ a + (m - 1 ) d = 164
या 8 + (m - 1 ) 6 = 164
या 8 + 6m - 6 = 164
या 6m = 162
या m = \(\frac{162}{6}\) = 27
अतः m = 27.

प्रश्न 14.
8 और 26 के बीच ऐसी 5 संख्याएँ डालिए ताकि प्राप्त अनुक्रम समान्तर श्रेढी बन जाए ।
हल:
माना कि 8 और 26 के बीच पाँच संख्याएँ A₁, A₂, A₃, A₄ तथा A₅ डाली गई हैं जिससे प्राप्त समान्तर श्रेढी 8, A₄, A₅, A₆, होगी।
इसमें प्रथम पद (a) = 8, अंतिम पद (l) = 26
यदि सार्वअन्तर d हो तो
26 = a + (n - 1) d = 8 + (7 - 1 ) d
26 = 8 + 6d
या 6d = 18 ∴ d = \(\frac{18}{6}\) = 3
अतः दूसरा पद (A₁) = a + d = 8 + 3 = 11
तीसरा पद (A₂) = 11 + 3 = 14
चौथा पद (A₃) = 14 + 3 = 17
पाँचवाँ पद (A₄) = 17 + 3 = 20
छठा पद (A₅) = 20 + 3 = 23
अतः 8 व 26 के बीच पाँच संख्याओं क्रमश: A₁, A₂, A₃, A₄ व A₅ के मान क्रमश: 11, 14, 17, 20 व 23 हैं।

प्रश्न 15.
यदि \(\frac{a^n+b^n}{a^{n-1}+b^{n-1}}\), a तथा b के मध्य समान्तर माध्य हो तो का मान ज्ञात कीजिए।
हल:
a तथा b के मध्य समान्तर माध्य = \(\frac{a+b}{2}\)
लेकिन प्रश्नानुसार \(\frac{a^n+b^n}{a^{n-1}+b^{n-1}}=\frac{a+b}{2}\)
या 2aⁿ + 2bⁿ = aⁿ + a^{n - 1} b + ab^{n - 1} + bⁿ
या aⁿ - a^{n - 1}b - ab^{n - 1} + bⁿ = 0
या a^{n - 1} (a - b) - b^{n - 1} (a - b) = 0
या (a - b) [a^{n - 1} - b^{n - 1}] = 0 [∵ a ≠ b]
या a^{n - 1} - b^{n - 1} = 0
यां a^{n - 1} = b^{n - 1}
या \(\left(\frac{a}{b}\right)^{n-1}\) = 1 = \(\left(\frac{a}{b}\right)^0\)
या n - 1 = 0
∴ n = 1

प्रश्न 16.
m संख्याओं को 1 तथा 31 के रखने पर प्राप्त अनुक्रम एक समान्तर श्रेढी है और 7वीं एवं (m - 1 ) वीं संख्याओं का अनुपात 5:9 है, तो mm का मान ज्ञात कीजिए ।
हल:
माना कि 1 तथा 31 के बीच m संख्याएँ क्रमश: A₁, A₂, A₃, ..................., A_m हैं अतः समान्तर श्रेढी जो प्राप्त होगी-
1, A₁, A₂, A₃, ................... A_m, 31
यहाँ a = 1, T_{m + 2} = 31
या a + (m + 2 - 1) d = 31
या 1 + (m + 1) d = 31

या 9m + 1899 = 155m - 145
या 9m - 155m = - 145 - 1899
या - 146m = - 2044
या m = \(\frac{2044}{146}\) = 14
m = 14

प्रश्न 17.
एक व्यक्ति ऋण का भुगतान 100 रुपए की प्रथम किस्त से शुरू करता है। यदि वह प्रत्येक किस्त में 5 रुपए प्रति माह बढ़ाता है तो 30वीं किस्त की राशि क्या होगी ?
हल:
प्रथम किस्त (a) = 100 रुपए
प्रत्येक माह किस्त में वृद्धि = सार्वअन्तर (d) = 5 रुपए
∴ 30वीं किस्त = समान्तर श्रेणी का 30वाँ पदं
= a + (n - 1) d
= 100+ (30 - 1) 5 [∵ n = 30]
= 100 + 29 × 5
= 100 + 145 = 245 रुपये.
अतः 30वीं किंस्त की राशि = 245 रुपये

प्रश्न 18.
एक बहुभुज के दो क्रमिक अंतः कोणों का अन्तर 5° है। यदि सबसे छोटा कोण 120° हो, तो बहुभुज की भुजाओं की संख्या ज्ञात कीजिए ।
हल:
हम जानते हैं कि n भुजाओं वाले बहुभुज के अन्तःकोणों का योग
= (2n - 4) × 90°
= 180 n - 360° ....... (i)
अब प्रश्नानुसार कोणों का क्रम = 120°, 125°, 130°, ........
यहाँ a = 120°, d = 125 - 120 = 5°
∵ S_n = \(\frac{n}{2}\) [2a + (n - 1)d]
या 180n - 360° = \(\frac{n}{2}\) [2 × 120 + (n - 1)5]
या 2(180n - 360°) = n (240 + 5n - 5)
या 360n - 720 = 240n + 5n² - 5n
या 360n - 720 = 5n² + 235n