RBSE Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 9 Sequences and Series Ex 9.2

Question 1.
Find the sum of odd integers from 1 to 2001.
Answer:
Sequence of odd integers from 1 to 2001
1, 3, 5, 7, 9, ....................., 2001
Let sequence has n terms, then
First term a₁ = 1, common difference d = 3 - 1 = 2
Thus, n^th term = a_n = a₁ + (n - 1) d
= 1 + (n - 1) × 2
= 2n - 1
But n^th term will be 2001 (nth term = last term)
Then 2n - 1 = 2001
or 2n = 2001 + 1
or 2n = 2002
∴ n = 1001
Thus, there are 1001 terms in the sequence.

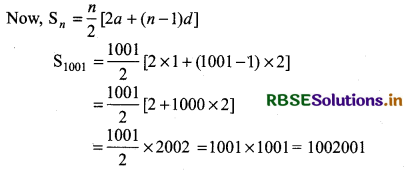
Thus, sum of odd integers from 1 to 2001 = 1002001

Question 2.
Find the sum of all natural numbers lying between 100 and 1000 which are multiples of 5.
Answer:
Between 100 and 1000 multiples of 5 are 105, 110, 115, ................, 995.
Let the sequence has n terms, then
First term a₁ = 105.
Common difference d = 110 - 105 = 5
n^th term, a_n = a₁ + (n - 1)d
= 105 + (n - 1) × 5
= 105 + 5n - 5
= 5n + 100
Here, n^th term is last term which is 995 in sequence.
So, 5n + 100 = 995
⇒ 5n = 995 - 100
⇒ 5n = 895
⇒ n = \(\frac{895}{5}\)
∴ n = 179
Thus, there will be 179 terms in sequence.
Sum of n terms, S_n = \(\frac{n}{2}\)(a + l)
Sum of 179 terms, S₁₇₉ = \(\frac{179}{2}\) (105 + 995)
= \(\frac{179}{2}\) × 1100
= 179 × 550 = 98450
Thus, sum of natural numbers, between 10 and 1000 which are multiples of 5 = 98450

Question 3.
In an A.P., the first term is 2 and the sum of the first five terms is one-fourth of the next five terms. Show that 20^th term is - 112.
Answer:
Given, first term. a1 = 2 and common difference = d
Then sum of first 5 terms = a₁ + a₂ + a₃ + a₄ + a₅
Thus,sum of n terms, S_n = \(\frac{n}{2}\) [2a + (n - 1)d]
∴ Sum of first 5 terms,
S₅ = \(\frac{5}{2}\)[2 × 2 + (5 - 1)d] (∵ Given, first term a =2)
⇒ S₅ = \(\frac{5}{2}\) [4 + 4d]
⇒ S₅ = 10 + 10d ............. (1)
Sum of next 5 terms from first 5 terms
= a₆ + a₇ + a₈ + a₉ + a₁₀
= (a₁ + 5d )+ (a₁ + 6d) + (a₁ + 7d) + (a₁ + 8d) + (a₁ + 9d)
= (2 + 5d) + (2 + 6d) + (2 + 7d) + (2 + 8d) + (2 + 9d) (∵ a₁ = 2)
= 10 + 35d .................... (2)
Now, we have
Sum of first 5 terms = \(\frac{1}{4}\) × sum of next 5 terms .
Then 10 + 10d = \(\frac{1}{4}\)(10 + 35d) [From (I) and (2)]
⇒ 40 + 40d = 10 + 35d
⇒ 40d - 35d = 10 - 40
⇒ 5d = - 30
∴ d = - 6
Then 20th term = a₁ + (20 - 1)d
[By formula a_n = a + (n - 1)d]
= 2 + 19 × (- 6) .
= 2 - 114
= - 112
Thus, 20th term = - 112
Hence Proved.

Question 4.
How many terms of A.P. - 6, - \(\frac{11}{2}\), - 5, ............., are needed to give the sum - 25?
Answer:
Let sum of n terms - 6, - \(\frac{11}{2}\), - 5 ........... is - 25.
Here, first term a₁ = - 6, sum of n terms S_n = - 25

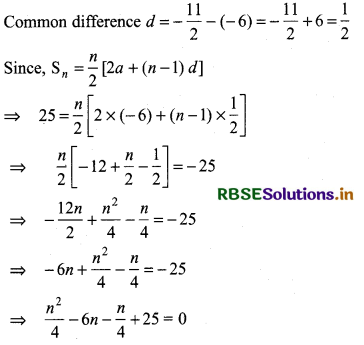
⇒ n² - 24n - n + 100 = 0
⇒ n² - 25n + 100 = 0
⇒ n² - (20 + 5)n + 100 = 0
⇒ n² - 20n - 5n + 100 = 0
⇒ n(n - 20) - 5(n - 20) = 0
⇒ (n - 20) (n - 5) = 0
Either n - 20 = 0 ⇒ n = 20
or n - 5 = 0 ⇒ n = 5 .
Thus, no. of terms will be 5 or 20.

Question 5.
In an A.P., if pth term is \(\frac{1}{q}\) and qth term is \(\frac{1}{p}\), then prove that the sum of first pq terms is \(\frac{1}{2}\) (pq + 1), where p ≠ q.
Answer:
Let first term of the A.P. is a and d be the common difference
Now, pth term = a + (p - 1)d = \(\frac{1}{q}\) ...... (1)
and qth term = a + (q - 1) d = \(\frac{1}{p}\) ......... (2)
[∵ a_n = a + (n - 1)d]
Subtracting equation (2) from (1),

Question 6.
If the sum of a certain number of terms of the A.P. 25, 22, 19, ... is 116. Find the last term.
Answer:
First term of given progression a₁ = 25
Common difference d = 22 - 25 = - 3
Let the sum of n terms of the progression be 116.

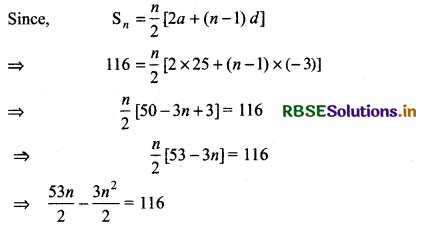
⇒ 3n² - 53n + 116 × 2 = 0
⇒ 3n² - 53n + 232 = 0
⇒ 3n² - (24 + 29)n + 232 = 0
⇒ 3n² - 24n - 29n + 232 = 0
⇒ 3n (n - 8) - 29 (n - 8) = 0
⇒ (3n - 29) (n - 8) = 0
Either 3n - 29 = 0 ⇒ n = \(\frac{29}{3}\)
⇒ n - 8 = 0 ⇒ n = 8
Since no. of terms can only be whole number not rational so n ≠ \(\frac{29}{3}\)
So, n = 8
Let last term or 8th term = a₁ + (n - 1)d.
= 25 + (8 - 1) × (- 3)
= 25 - 21 = 4
Thus, last term of progression is 4.

Question 7.
Find sum of n terms of A.P. whose k^th term is 5k + 1.
Answer:
Let first term of A.P. is a and d its common difference
We have, k^th term of progression = 5k +1
⇒ a_k = 5k + 1
Putting k = 1
First term of the progression a₁ = 5 × 1 + 1 = 6
Putting k = 2
Second term of the progression a₂ = 5 × 2 + 1 = 11
Putting k = 3
Third term of the progression a₃ = 5 × 3 + 1 = 16
Common difference of A.P. d = a₂ - a₁ = a₃ - a₂
⇒ common difference = 11 - 6 = 16 - 11 = 5

Question 8.
If the sum of n terms of an A.P. is (pn + qn²), where p and q are constants, then find the common difference.
Answer:
Let the first term of the progression be a1 and the common difference is d.
According to question,
Sum of n terms of AP.
S_n = pn + qn² (Given)
Sum of (n - 1) terms
S_{n - 1} = p(n - 1) + q(n - 1)²
Since, n^th term, a_n = sum of n terms - sum of (n - 1) terms
⇒ a_n = S_n - S_{n - 1}
⇒ n^th term, a_n = pn + qn² - [p(n - 1) + q(n - 1)²]
= pn + qn² - [pn - p + q(n² - 2n + 1)]
= pn + qn² - pn + p - qn² + 2qn - q
n^th term, a_n = 2qn + p - q
Putting n = 1, 2, 3 ..................
1^st term a₁ = 2q + p - q = (q + p)
2^nd term a₂ = 2q × 2 + p - q
a₂ = 4q + p - q = (3q + p)
and 3^rd term a₃ = 2q × 3 + p - q
= 6q + p - q = 5q + p
........................................................
........................................................
........................................................
Common.difference d = a₂ - a₁
= 3q + p - (q + p)
∴ d = 3q + p - q - p = 2q
Thus, required common difference of the progression is d = 2q.

Question 9.
The sum of n terms of two A.P. are in the ratio 5n + 4 : 9n + 6 Find the ratio of their 18^th terms.
Answer:
Let first term of AP. 1 is a₁ and common difference is d₁
Then n^th term of progression
a _n = a₁ + (n - 1) d₁ ................... (1)
Sum of n terms of this progression
S_n = \(\frac{n}{2}\)[2a₁ + (n - 1)d₁] ....................... (2)
Now, let first term of ASP. II is a, and common difference is d₂
Then n^th term of progression
A_n = a₂ + (n - 1)d₂ ........................... (3)
Sum of n terms of second A.P.
S_n = \(\frac{n}{2}\)[2a₂ + (n - 1)d₂] ........................ (4)
Dividing equation (2) by (4),

n^th term of progression by equation (1)
= a₁ + (n - 1)d₁
So, 18^th term = a₁ + (18 - 1)d₁
= a₁ + 17d₁
Similarly, 18^th term of second progression
= a₂ + (18 - 1) d₂
= a₂ + 17d₂
Then ratio of 18th terms of two progressions
= \(\frac{a_1+17 d_1}{a_2+17 d_2}\) ......................... (6)
So, clearly from equation (5) ratio of 18^th terms of progression can be find if coefficient of d₁ and d₂ are 17.
i.e., \(\frac{n-1}{2}\) = 17
⇒ n - 1 = 2 × 17
⇒ n - 1 = 34
∴ n = 34 + 1 = 35
Now, putting n = 35 in equation (5),

Question 10.
If the sum of first p terms of an A.P. is equal to the sum of the first q terms then find the sum of the first (p + q) terms.
Answer:
Let first term of A.P. is a₁ and common difference is d
∴ Sum of first p terms

Question 11.
Sum of the first p, q and r terms of an A.P. are a, b an c respectively. Prove that
\(\frac{a}{p}\) (q - r) + \(\frac{b}{q}\) (r - p) + \(\frac{c}{r}\) (p - q) = 0
Answer:
Let the first term of given A.P. is a1 and the common difference is d, then we have

Question 12.
The ratio of the sums of m and n terms of an A.P is m² : n². Show that the ratio of m^th and n^th term is (2m - 1) : (2n - 1).
Answer:
If a be the first term of A.P. and d be the common difference.
Sum of m terms S_m = \(\frac{m}{2}\)[2a + (m - 1) d] ...................... (1)
Sum of n terms
S_n = \(\frac{n}{2}\)[2a + (n - 1) d] ............... (2)
We have,
\(\frac{\mathrm{S}_m}{\mathrm{~S}_n}=\frac{m^2}{n^2}\)
Dividing equation (1) by (2),

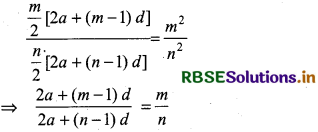
⇒ n[2a + (m - 1)d] = m[2a + (n - 1)d]
⇒ 2an + n(m - 1)d = 2am + m(n - 1)d
⇒ 2an - 2am = m(n - 1)d - n(m - 1)d
⇒ 2a(n - m) = [m(n - 1) - n(m - 1)]d
⇒ 2a(n - m) = [mn - m - nm + n]d
2a (n - m) = (n - m) d
⇒ 2a = d
⇒ d = 2a ................. (1)

Thus, m^th term : n^th = (2m - 1) : (2n - 1)
Hence proved.

Question 13.
If the sum of n terms of an A.P. is 3n² + 5n and its m^th term is 164, then find the value of m.
Answer:
Sum of n terms of A.P.
S_n = 3n² + 5n .
Sum of (n - 1) terms of AP.
S_{n - 1} = 3(n - 1)² + 5(n - 1)
then n th term of A.P. = S_n - S_{n - 1}
a_n = 3n² + 5n - [3(n - 1)² + 5(n - 1)]
= 3n² + 5n - [3n² + 3 - 6n + 5n - 5]
= 3n² + 5n - 3n² + n + 2
⇒ a_n = 6n + 2
and a_m = 6m + 2
Given mth term =164
6m + 2 = 164
⇒ 6m = 164 - 2 = 162
∴ m = \(\frac{162}{6}\) = 27
Thus, m = 27

Question 14.
Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.
Answer:
Let five numbers between 5 and 26 are
A₁, A₂, A₃, A₄ and A₅
Then A₁, A₂, A₃, A₄ and A₅, 26 will be in A.P.
Now, total terms in progression = 7
7^th term = 26, first term = 8 = a₁
If common difference of series is d, then
7^th term = a₁ + (7 - 1)d [∵ a =a+(n—l)d]
⇒ 7th term = 8 + 6d = 26
⇒ 8 + 6d = 26
⇒ 6d = 26 - 8
⇒ 6d = 18
⇒ d = \(\frac{18}{6}\) = 3
Thus A₁ = d + 8 = 3 + 8 = 11
A₂ = A₁ + d
= 11 + 3 = 14
A₃ = A₁ + 2d
= 11 + 2 × 3
= 11 + 6 = 17
A₄ = A₁ + 3d
= 11 + 3 × 3
= 11 + 9
= 20
A₅ = A₁ + 4d
= 11 + 3 × 4
⇒ A₅ = 11 + 12 = 23
Thus, between 8 and 26 required five numbers are 11, 14, 17, 20 and 23.

Question 15.
If \(\frac{a^n+b^n}{a^{n-1}+b^{n-1}}\) is the A.M. between a and b, then find the value of n.
Answer:
We know that A.M. between a and b
= \(\frac{a+b}{2}\)
But A.M. between a and b
= \(\frac{a^n+b^n}{a^{n-1}+b^{n-1}}\) (Given)
Then two A.M's will be same
So, \(\frac{a+b}{2}=\frac{a^n+b^n}{a^{n-1}+b^{n-1}}\)
⇒ (a + b) (a^{n - 1} + b^{n - 1}) = 2(aⁿ + bⁿ)
(By cross-multiplication)
⇒ a × a^{n - 1} + ab^{n - 1} + ba^{n - 1} + b × b^{n - 1} = 2aⁿ + 2bⁿ
aⁿ + ab^{n - 1} + ba^{n - 1} + bⁿ = 2aⁿ + 2bⁿ
⇒ ab^{n - 1} + ba^{n - 1} = 2aⁿ - aⁿ + 2bⁿ - bⁿ = aⁿ + bⁿ
⇒ aⁿ - ba^{n - 1} + bⁿ - ab^{n - 1} = 0
⇒ a^{n - 1} (a - b) + b^{n - 1} (b - a) = 0
⇒ a^{n - 1} (a - b) - b^{n - 1} (a - b) = 0
⇒ (a - b) [a^{n - 1} - b^{n - 1}] = 0
⇒ a^{n - 1} = b^{n - 1} where a ≠ b

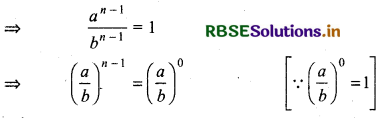
Comparing powers on both sides 
n - 1 = 0
Then n = 1

Question 16.
Between I and 31, m numbers have been inserted in such a way that the resulting sequence is an A.P. and the ratio 0f 17^th and (m - 1)^th numbers is 5 : 9. Find the value of m.
Answer:
Let between 1 and 31, m numbers are,
1 + d, 1 + 2d, 1 + 3d, ............. 1 + md.
Then 1, 1 + d, 1 + 2d, 1 + 3d .......... 1 + md, 31 will be in A.P.
Where d is common difference of terms
Now, 7^th term of sequence = 1 + 7d
and (m - 1)^th number = 1 + (m - 1) d
We have,
\(\frac{1+7 d}{1+(m-1) d}=\frac{5}{9}\)
Thus 9 + 63d = 5 + 5(m - 1)d
⇒ 9 + 63d = 5 + 5md - 5d
⇒ 63d + 5d = 5 - 9 + 5 md
⇒ 68d - 5md = -4
⇒ d(68 - 5m) = - 4
⇒ d = - \(\frac{4}{68-5 m}\)
∴ d = \(\frac{4}{5 m-68}\) ............ (1)
Number of terms in sequence = (m + 2)
Now, (m + 2)^th term = 31
⇒ 1 + (m + 2 - 1)d = 31
⇒ 1 + (m + 1)d = 31
⇒ (m + 1)d = 31 - 1
⇒ (m + 1)d = 30
∴ d = \(\frac{30}{(m+1)}\)
Putting value of d in equation (1)
\(\frac{30}{m+1}=\frac{4}{5 m-68}\)
⇒ 30(5m - 68) = 4(m + 1)
⇒ 150m - 2040 = 4m + 4
⇒ 150m - 4m = 2040 + 4
⇒ 146m = 2044
⇒ m = \(\frac{2044}{146}\) = 14
Thus, m = 14

Alternative Method:
If between 1 and 31, m A.M. are A₁, A₂, A₃, A₄, ......................, A_m then number of terms will be (m + 2).
⇒ 1, A₁, A₂, A₃, A₄, A₅, ................... A_m, 31 will be in A.P.
∴ a_{m + 2} ⇒ 31 ⇒ 1 + (m + 2 - 1)d = 31
⇒ 1 + (m + 1)d = 31
⇒ (m + 1)d = 31 - 1
⇒ (m + 1)d = 30

⇒ 9m + 1899 = 155m - 145
⇒ 146m = 2044
∴ m = 14

Question 17.
A man starts repaying a loan as first instalment of ₹ 100. If he increases the instalment by ₹ 5 every month, what amount he will pay in the 30^th instalment?
Answer:
1st instalment of repayment, a = ₹ 100
Difference of each instalment (amount), d = ₹ 5
Now, amount 0f 30th instalment = a + (n - 1)d
= 100 + (30 - 1) × 5, where n = 30
= 100 + 29 × 5
= 100 + 145 = 245
Thus, amount of 30th instalment = ₹ 245.

Question 18.
The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 1200, find the number of the sides of the polygon.
Answer:
Let the number of sides in polygon be n.
Interior angles in polygon = n
Sum of interior angles of polygon = 90° × (2n - 4)
Now, smallest angles A = 120°
other angle A₂ = 120° + 50° = 125°
(Difference in angles 5°)

But sum of all n angles = 90° × (2n - 4) ................. (2)
Thus, \(\frac{n}{2}\)(5n + 235) = 90° (2n - 4)
From equation (1) and equation (2)
⇒ \(\frac{n}{2}\) (5n + 235) = (180n - 360)
⇒ 5n² + 235n = 2(180n - 360)
⇒ 5n² + 235n = 360n - 720
⇒ 5n² + 235n - 360n + 720 = 0
⇒ 5n² - 125n + 720 = 0
⇒ n² - 25n + 144 = 0
⇒ n² - (16 + 9)n + 144 = 0
⇒ n² - 16n - 9n + 144 = 0
⇒ n(n - 16)- 9(n - 16) = 0
⇒ (n - 16)(n - 9) = 0
Either n - 16 = 0 ⇒ n = 16
or n - 9 = 0 ⇒ n = 9
∴ n = 16, n = 9
So, number of sides in polygon = 9 or 16
But 16 sides are not possible.
Since a₁₆ = a + 15d [Given, d = 5]
= 120 + 15 × 5
= 120 + 75
= 195°
which is not possible
Thus, number of sides in polygon = 9