RBSE Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 9 Sequences and Series Ex 9.1

Write the first five terms of each of the sequences in exercises 1 to 6 whose n^th terms are:

Question 1.
a_n = n(n + 2)
Answer:
Putting n = 1, 2, 3, 4, 5
a₁ = 1 × (1 + 2) = 3
a₂ = 2 × (2 + 2) = 8
a₃ = 3 × (3 + 2) = 15
a₄ = 4 × (4 + 2) = 24
a₅ = 5 × (5 + 2) = 35
Thus, first five terms of the sequence are 3, 8, 15, 24, 35.

Question 2.
a_n = \(\frac{n}{n+1}\)
Answer:
Putting n = 1, 2, 3, 4, 5

Thus, first five terms of the sequence are \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}\)

Question 3.
a_n = 2ⁿ
Answer:
Putting n = 1, 2, 3, 4, 5
a₁ = 2¹ = 2
a₂ = 2² = 4
a₃ = 2³ = 8
a₄ = 2⁴ = 16
a₅ = 2⁵ = 32
Thus, first five terms of the sequence are 2, 4, 8, 16, 32

Question 4.
a_n = \(\frac{2 n-3}{6}\)
Answer:
Putting n = 1, 2, 3, 4, 5

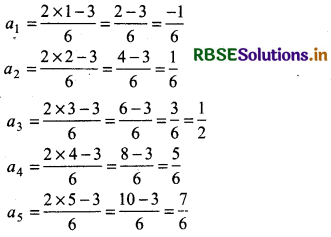
Thus, first five terms of the sequence are \(\frac{-1}{6}, \frac{1}{6}, \frac{1}{2}, \frac{5}{6}, \frac{7}{6}\).

Question 5.
a_n = (- 1)^{n - 1} 5^{n + 1}
Answer:
Putting n = 1, 2, 3, 4, 5
a₁ = (- 1)^{1 - 1} 5^{1 + 1}
= (- 1)⁰ 5² = 25
a₂ = (- 1)² 5^{2 + 1}
= (- 1)¹ 5³ = - 125
a₃ = (- 1)^{3 - 1} 5^{3 + 1}
= (- 1)² 5⁴ = 625
a₄ = (- 1)^{4 - 1} 5^{4 + 1}
= (- 1)³ 5⁵ = - 3125
a₅ = (- 1)^{5 - 1} 5^{5 + 1}
= (- 1)⁴ 5⁶ = 15625
Thus, first five terms of the sequence are 25, - 125, 625, - 3125, 15625

Question 6.
a_n = n\(\frac{n^2+5}{4}\)
Answer:
Putting n = 1, 2, 3, 4, 5

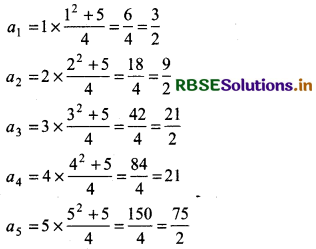
Thus, five terms of the sequence are \(\frac{3}{2}, \frac{9}{2}, \frac{21}{2}, 21, \frac{75}{2}\)

Find the indicated terms in each of the sequences in exercise 7 to 10 whose n^th term are:

Question 7.
a_n = 4n - 3;a₁₇, a₂₄
Answer:
n^th term of given the sequence a_n = 4n - 3
Putting n = 17 and n = 24 in a_n = 4n - 3
a₁₇ = 4 × 17 - 3
= 68 - 3
= 65
and a₂₄ = 4 × 24 - 3
= 96 - 3
= 93
Thus, a₁₇ = 65 and a₂₄ = 93

Question 8.
a_n = \(\frac{n^2}{2^n}\); a₇
Answer:
n^th term of the given sequence a_n = \(\frac{n^2}{2^n}\)
Putting n = 7, we get
a₇ = \(\frac{7^2}{2^7}\) = \(\frac{49}{128}\)
Thus, the required term a₇ = \(\frac{49}{128}\)

Question 9.
a = (- 1)^{n - 1} n³; a₉
Answer:
n^th term of the given sequence
a_n = (- 1)^{n - 1} n³
Putting n = 9, we get
a = (- 1)^{9 - 1} 9³
= (- 1)⁸ 9³ = 729
Thus, required term a₉ = 729

Question 10.
a_n = \(\frac{n(n-2)}{n+3}\); a₂₀
Answer:
n^th term of the given sequence
a_n = \(\frac{n(n-2)}{n+3}\)
Putting n = 20, we get
a₂₀ = \(\frac{20(20-2)}{20+3}=\frac{20 \times 18}{23}=\frac{360}{23}\)
Thus, the required term a₂₀ = \(\frac{360}{23}\)

Write the first five terms of each of the sequences in exercise 11 to 13 and obtain the corresponding series.

Question 11.
a₁ = 3, a_n = 3a_{n - 1} + 2, for all n > 1.
Answer:
Putting n = 2, 3, 4, 5 in a_n = 3a_{n - 1} + 2
a₂ = 3a_{2 - 1} + 2
= 3a₁ + 2
= 3 × 3+ 2 (∵ a₁ = 3)
= 11

a₃ = 3 × a_{3 - 1} + 2
= 3a₂ + 2
= 3 × 11 + 2 (∵ a₂ = 11)
= 35

a4 = 3a_{4 - 1} + 2
= 3 × a₃ + 2
= 3 × 35 + 2 (∵ a₃ = 35)
105 + 2 = 107

a₅ = 3 × a_{5 - 1} + 2
= 3 × a₄ + 2
= 3 × 107 + 2 (∵ a₄ = 107)
= 321 + 2 = 323
Thus, five terms of sequence are 3, 11, 35, 107, 323 and corresponding series is 3 + 11 + 35 + 107 + 323....

Question 12.
a₁ = - 1, a_n = \(\frac{a_{n-1}}{n}\), where n ≥ 2
Answer:

Question 13.
a₁ = a₂ = 2, a_n = a_{n - 1} - 1, n > 2
Answer:
Given a₁ = a₂ = 2, a_n = a_{n - 1} - 1
Here, first term a₁ = second term a₂ = 2
Putting n = 3, 4, 5 in a_n = a_{n - 1}
a₃ = a_{3 - 1} - 1
= a₂ - 1
∴ a₃ = 2 - 1 = 1 (∵ a₂ = 2)
a₄ = a₄ - 1
= 1 - 1 (∵ a₃ = 1)
= 0
a₅ = a₅ - 1 - 1
= a₄ - 1 .
= 0 - 1 [∵ a₄ = 0]
= - 1
Thus, five terms of sequence are 2, 2, 1, 0, - 1 and corresponding series is 2 + 2 + 1 + 0 + (- 1) + ..................

Question 14.
The Fibonacci sequence is defined by:
1 = a₁ = a₂ and a_n = a_{n - 1} + a_{n - 2}, n > 2 find \(\frac{a_{n+1}}{a_n}\) for n = 1, 2, 3, 4, 5, ..............
Answer:
Given: 1 = a₁ = a₂ and a_n = a_{n - 1} + a_{n - 2}
(Fibonacci sequence)
For n = 3, 4, 5, 6
n^th term a_n = a_{n - 1} + a_{n - 2}
Putting n = 3, we get
a₃ = a_{3 - 1} + a_{3 - 2}
= a₂ + a₁
= 1 + 1 (∵ a₁ = a₂ = 1)
= 2
Putting n = 4, we get
a₄ = a_{4 - 1} + a_{4 - 2}
= a₃ + a₂
= 2 + 1 (∵ a₃ = 2, a₂ = 1)
= 3
Putting n = 5, we get
a₅ = a_{5 - 1} + a_{5 - 2}
= a₄ + a₃
= 3 + 2 (∵ a₄ = 3, a₃ = 2)
= 5
And Putting n = 6, we get
a₆ = a_{6 - 1} + a_{6 - 2}
= a₅ + a₄
= 5 + 3 (∵ a₅ = 5, a₄ = 3)
= 8
Now,