RBSE Solutions for Class 11 Maths Chapter 8 क्रमचय और संचयं विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 8 द्विपद प्रमेय विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 8 द्विपद प्रमेय विविध प्रश्नावली

प्रश्न 1.
यदि (a + b) के प्रसार में प्रथम तीन पद क्रमशः 729, 7290 तथा 30375 हों तो a, b और n ज्ञात कीजिए।
हल:
(a + b)ⁿ के प्रसार में प्रथम तीन पद क्रमशः aⁿ, ⁿC₁ a^{n - 1} b तथा ⁿC₂ a^{n -2} b² हैं। प्रश्नानुसार
aⁿ = 729 ............... (1)
n a^{n - 1} b = 7290 .................. (2)

प्रश्न 2.
यदि (3 + ax)⁹ के प्रसार में x² तथा x³ के गुणांक समान हों, तो a का मान ज्ञात कीजिए।
हल:
(3 + ax)⁹ = ⁹C₀ (3)⁹ + ⁹C₁ (3)⁸ (ax)¹ + ⁹C₂ (3)⁷ (ax)² + ⁹C₃ (3)⁶ (ax)³ + ..................... + ⁹C₉ . (ax)⁹
उक्त प्रसार में x² का गुणांक = ⁹C₂ (3)⁷ (ax)²
तथा x³ का गुणांक = ⁹C₃ (3)⁶ (ax)³
प्रश्नानुसार ⁹C₂ (3)⁷ (ax)² = ⁹C₃ (3)⁶ (ax)³
या ⁹C₂ (3) = ⁹C₃ a

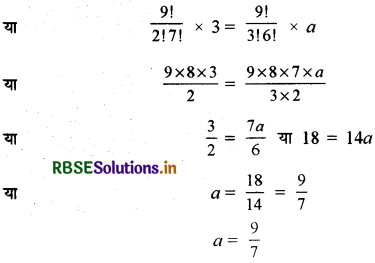
प्रश्न 3.
द्विपद प्रमेय का उपयोग करते हुए गुणनफल (1 + 2x)⁶ (1 - x)⁷ में x⁵ का गुणांक ज्ञात कीजिए ।
हल:
द्विपद प्रमेय के आधार पर
(1 + 2x)⁶ = ⁶C₀ + ⁶C₁ (2x)¹ + ⁶C₁ (2x)² + ⁶C₃ (2x)³ + ⁶C₄ (2x)⁴ + ⁶C₅ (2x)⁵ + ⁶C₁ (2x)⁶
= 1 + 6 (2x) + 15 (4x²2) + 20 (8x³) + 15 (16x⁴) + 6 (32) x⁵ + 64x⁶
= 1 + 12x + 60x² + 160x³ + 240x⁴ + 192x⁵ + 64x⁶
इसी प्रकार
(1 - x)⁷ = ⁷C_o - ⁷C₁ x¹ + ⁷C₂ x² - ⁷C₃ x³ + ⁷C₄ x⁴ - ⁷C₅ x⁵ + ⁷C₆ x⁶ - ⁷C₇ x⁷
= 1 - 7x + 21x² - 35x³ + 35x⁴ - 21x⁵ + 7x⁶ - x⁷
अतः प्रश्नानुसार (1 + 2x)⁶ . (1 - x)⁷
= (1 + 12x + 60x² + 160x³ + 240x⁴ + 192x⁵ + 64x⁶) . (1 - 7x + 21x² - 35x³ + 35x⁴ - 21x⁵ + 7x⁶ - x⁷)
इनके गुणनफल में से X वाले पदों को लेने पर
1 . (- 21x⁵) + (12x) (35x⁴) + (60x²) (- 35x²) + (160x³) (21x²) + (240x⁴) (-7x) + (192x⁵) . 1
अतः x⁵ वाले पदों का गुणांक = - (21) + (12) (35) + (60) (- 35) + (160) (21) + (240) (- 7) + 192
= - 21 +420 2100 + 3360 – 1680 + 192
= 3972 - 3801
= 171

प्रश्न 4.
यदि a और b भिन्न-भिन्न पूर्णांक हों, तो सिद्ध कीजिए कि (aⁿ - bⁿ) का एक गुणनखण्ड (a - b) है, जबकि n एक धन
पूर्णांक है। [संकेत : aⁿ = (a - b + b)ⁿ लिखकर प्रसार कीजिए। ]
हल:
a = b + (a - b)
∴ aⁿ = [b + (a - b)]ⁿ
= bⁿ + ⁿC₁ b^{n - 1} (a - b) + ⁿC₂ b^{n - 2} (a - b)² + ................ + ⁿC_n (a - b)ⁿ
∴ aⁿ - bⁿ = ⁿC₁ bⁿ - 1 (a - b) + ⁿC₂ b^{n - 2} (a - b)² + .................. + ⁿC_n (a - b)ⁿ
= (a - b) [ⁿC₁ b^{n - 1} + ⁿC₂ b^{n - 2} (a - b) + ................. + ⁿC_n (a - b)^{n - 1}]
स्पष्ट होता है कि aⁿ - bⁿ का एक गुणनखण्ड (a - b) है।

प्रश्न 5.
(√3 + √2)⁶ - (√3 - √2)⁶ का मान ज्ञात कीजिए।
हल:
(√3 + √2)⁶ - (√3 - √2)⁶
माना कि √3 = a तथा √2 = b
∴ (a + b)⁶ = a⁶ + ⁶C₁ a⁵b + ⁶C₂ a⁴ b² + ⁶C₃ a³ b³ + ⁶C₅ ab⁵ +⁶C₆ ab⁶
= a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶ .................... (1)
इसी प्रकार (a - b)⁶ = a⁶ - 6a⁵b + 15a⁴b² - 20a³b³ + 15a²b⁴ - 6ab⁵ + b⁶ .................... (2)
∴ (a + b)⁶ - (a - b)⁶ = 2 (6a⁵b + 20a³b³ + 6ab³) = 4ab (3a⁴ + 10a²b² + 3b⁴)
यहाँ a व b का मान रखने पर
(√3+ √2)⁶ - (√3-√2)⁶
= 4√3 √2 |3(√3)⁴ + 10(√3)² (√2)² +3(√2)⁴]
= 4√6 (27 + 60 + 12)
= 4√6 × 99 = 396 √6

प्रश्न 6.
\(\left(a^2+\sqrt{a^2-1}\right)^4+\left(a^2-\sqrt{a^2-1}\right)^4\) का मान ज्ञात कीजिए ।
हल:

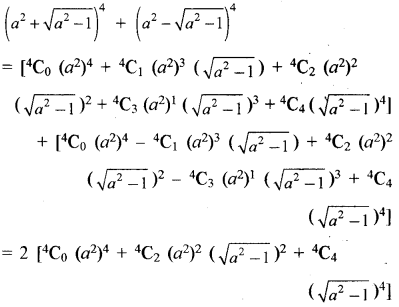
अन्य पदों की उपेक्षा करने पर
= 2 [a³ + 6a² \(\left(\sqrt{a^2-1}\right)^2 + \left(\sqrt{a^2-1}\right)^4\)]
= 2 [a³ + 6a² (a² - 1) + (a² - 1)²]
= 2 [a⁸ + 6a⁶ - 6a⁴ + a⁴ - 2a² + 1]
= 2 [a⁸ + 6a⁶ - 5a² - 2a² + 1]
= 2a⁸ + 12a⁶ - 10a⁴ - 4a² + 2

प्रश्न 7.
(0.99)⁵ के प्रसार के पहले तीन पदों का प्रयोग करते हुए इसका निकटतम मान ज्ञात कीजिए ।
हल:
(0.99)⁵ = (1 - 0.01)⁵
[⁵C₀ (1)³ + ⁵C₁ (1)⁴ (- 0.01) + ⁵C₂ (1)³ (- 0.01)² + ⁵C₃ (1)² (- 0.01)³ + 5C₄ (1) (- 0.01)4 + ⁵C₅ (- 0.01)³
प्रथम तीन पदों का प्रयोग करने पर
= [⁵C₀ (1)³ + ⁵C₁ (1)⁴ (- 0.01) + ⁵C₂ (1)³ (- 0.01)²]
= 1 + 5 (- 0.01) + 10 (- 0.01)²
= 10.05 + 0.001
= 1.001 - 0.05
= 0.951 (लगभग)

प्रश्न 8.
यदि \(\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^n\) के प्रसार में आरम्भ से 5वें और अन्त से 5वें पद का अनुपात √6 : 1 हो तो n ज्ञात कीजिए ।
हल:
(a + b)ⁿ के विस्तार में व्यापक पद T_r+1 = ⁿC_r a^n-r. b^r
अतः \(\left[\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right]^n\) के विस्तार में आरम्भ से पाँचवाँ पद
T₅ = T₄₊₁= ⁿC₄ (4√2 )^n-4\(\left[\frac{1}{\sqrt[4]{3}}\right]^4\) = ⁿC₄ \((2)^{\frac{n-4}{4}} \cdot\left(\frac{1}{3}\right)\)
प्रसार में पदों की कुल संख्या = n+ 1
अतः अन्त से 5वाँ पद = प्रारम्भ के [(n + 1) - 5 + 1]वें पद के
बराबर
अन्त से 5वां पद = प्रारम्भ से (n - 3 ) वाँ पद

प्रश्न 9.
\(\left(1+\frac{x}{2}-\frac{2}{x}\right)^4\), x ≠ 0 का द्विपद प्रमेय द्वारा प्रसार ज्ञात कीजिए ।
हल:

प्रश्न 10.
(3x² - 2ax + 3a²)³ का द्विपद प्रमेय से प्रसार ज्ञात कीजिए ।
हल:
(3x² - 2ax + 3a²)³
माना कि 2ax + 3a² = y
(3x² - 2ax + 3a²)³ = (3x² + y)³
= ³C₀ (3x²)³ + ³C₁ (3x²)². y + ³C₂ (3x²)1 . y² + ³C₃ y³
= 27x⁶ + 3 (9x⁴) y + 3 (3x²) y² + y³
= 27x⁶ + 27x⁴y + 9x²y² + y³
= 27x⁶ + 27x⁴ (− 2ax + 3a²) + 9x² (− 2ax + 3a²)² +(-2ax + 3a²)³
= 27x⁶ - 54ax⁵ + 81a²x⁴ + 9x² [(4a²x²) - 2 (ax) (3a²) + 9a⁴] + (3a²)³ - 3 (3a²)³ (2ax) + 3 (3a²) (2ax)² - (2ax)³
= 27x⁶ - 54ax³ + 81a²x² + 36a²x² - 108a³x³ + 81a⁴x² + 27a⁶ − 54a³. x + 36a²x² - 8a³x³
= 27x⁶ - 54ax² + 117a²x⁴ - 116a³x³ + 117a⁴x² - 54a³x + 27a⁶