RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 8 Binomial Theorem Miscellaneous Exercise

Question 1.
Find a, b and n in the expansion of (a + b)ⁿ first three terms of the expansion are 729, 7290, and 30375 respectively.
Answer:
In the expansion of (a + b)ⁿ
1st term T₁ = aⁿ = 729 .......... (1)
2nd term = T₂ = ⁿC₁ a^{n - 1}. b = 7290 ................ (2)
3rd term = T₃ = ⁿC₂ a^{n - 2}. b² = 30375 ......... (3)
Dividing equation (i) by (ii)

⇒ 12n - 12 = 10n
⇒ 2n = 12 ⇒ n = 6
Putting value of n in equation (1)
a⁶ = 729
⇒ a⁶ = 3⁶
On comparing
a = 3
Putting values of n and a in equation (4)
\(\frac{3}{6 \times b}=\frac{1}{10}\)
⇒ b = 5
Thus, a = 3, b = 5, n = 6

Question 2.
Find a if the coefficients of x² and x³ in the expansion of (3 + ax)⁹ are equal.
Answer:
T_{r + 1} = ⁹C_r 3^{9 - r} . a^r x^r
Putting r = 2
Coefficient of x² = ⁹C₂ 3⁷ . a² = 36.3⁷ a²
Putting r = 3
Coefficient of x³ = ⁹C₃ 3⁶ a³ = 84.3⁶.a³
∵ Coefficient of x² = Coefficient of x³ (given)
Thus, 36.3⁷ . a² = 84(3)⁶ a³

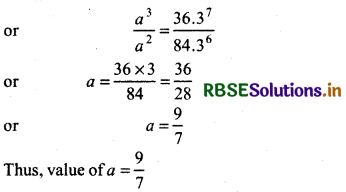
Question 3.
Find the coefficient of x⁵ in product (1 + 2x)⁶ (1 - x)⁷ using binomial theorem.
Answer:
Given expansion = (1 + 2x)⁶ (1 - x)⁷

Now, (1 + 2x)⁶ (1 - x)⁷
= (1 + 12x + 60x² + 160x³ + 240x⁴ + 192x⁵ + ...... ]
[1 - 7x + 21x² - 35x³ + 35x⁴ - 21x⁵ + ........]
Coefficient of x⁵ in above expansion
= [- 21 + 12 × 35 - 60 × 35 + 160 × 21 + 240(- 7) + 192 × 1]
= [- 21 + 420 - 2100 + 3360 - 1680 + 192]
= [- 3801 + 3972] = 171

Question 4.
If a and b are distinct integers prove that a - b is a factor of aⁿ - bⁿ, whenever n is a positive integer. [Hint: Write aⁿ = (a - b + b)ⁿ and expand.]
Answer:
∵ aⁿ - bⁿ = [(a - b) + b]ⁿ - bⁿ
Expanding by binomial theorem,

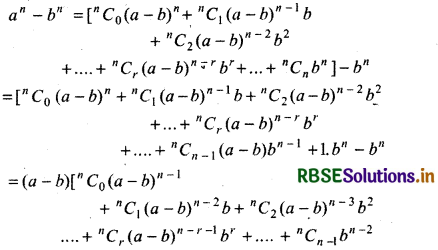
We see that (a - b) is a factor in R.H.S.
So, we can say that
aⁿ - bⁿ = (a - b)k
[Where k = ⁿC₀ (a - b)^{n - 1} + ....... ⁿC_{n - 1}b^{n - 2}]
It is clear that (a - b) is a factor of a - bⁿ
Hence proved

Question 5.
Evaluate (√3 + √2)⁶ - (√3 - √2)⁶
Answer:
By expansion of binomial theorem,

Question 6.
Find the value of
(a² + \(\sqrt{a^2-1}\))⁴ + (a² - \(\sqrt{a^2-1}\))⁴.
Answer:
By Binomial theorem,

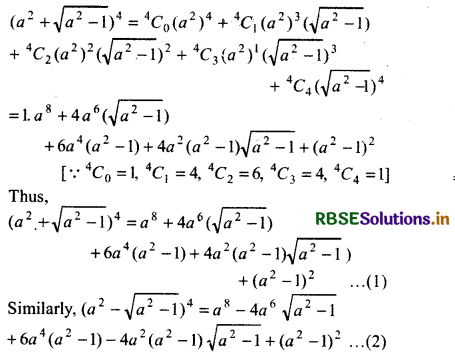
Adding (1) and (2).
(a² + \(\sqrt{a^2-1}\))⁴ + (a² - \(\sqrt{a^2-1}\))⁴.
= 2a⁸ + 12a⁴ (a² - 1) + 2(a² - 1)²
= 2a⁸ + 12a⁴ (a² - 1) + 2(a⁴ - 2a² + 1)
= 2a⁸ + 12a⁶ - 12a⁴ + 2a⁴ - 4a² + 2
= 2a⁸ + 12a⁶ - 10a⁴ - 4a² + 2
Thus, (a² + \(\sqrt{a^2-1}\))⁴ + (a² - \(\sqrt{a^2-1}\))⁴
= 2a⁸ + 12a⁶ - 10a⁴ - 4a² + 2
= 2(a⁸ + 6a⁶ - 5a⁴ - 2a² + 1)

Question 7.
Find an approximation of (0.99)⁵ using the first three terms of its expansion.
Answer:
∵ (0.99)⁵ = (1 - 0.01)⁵
Thus, by Binomial theorem
(1 - 0.01)⁵ = ⁵C₀ - ⁵C₁ (0.01) + ⁵C₂(0.01)²
(upto first 3 terms)
= 1 - 5(0.01) + 10(0.01)²
= 1 - 0.05 + 10 × 0.000 1
= 0.95 + 0.0010 = 0.9510
Thus, value of (0.99)⁵ = 0.9510

Question 8.
Find n if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of \(\left(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\right)^n\) is √6 : 1
Answer:

Question 9.
Expand using binomial theorem
\(\left(1+\frac{x}{2}-\frac{2}{x}\right)^4\), x ≠ 0.
Answer:

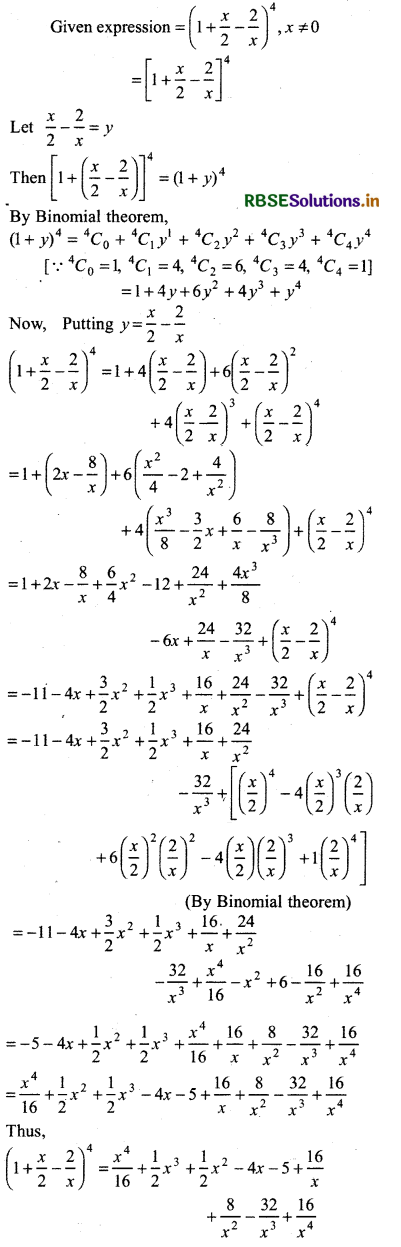
Question 10.
Find the expansion of (3x² - 2ax + 3a²)³ using binomial theorem.
Answer:
Given expression = (3x² - 2ax + 3a²)³
Let, y = 3x² - 2ax
Then by binomial theorem