RBSE Solutions for Class 11 Maths Chapter 8 द्विपद प्रमेय Ex 8.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 8 द्विपद प्रमेय Ex 8.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 8 द्विपद प्रमेय Ex 8.2

प्रश्न 1.
(x + 3)⁸ में x⁵ का
हल:
हम जानते हैं कि व्यापक पद T_{r + 1} = ⁿC_r a^{n - r} b^r
∴ (x + 3)⁸ का व्यापक पद = ⁸C_r, x^{8 - r} . 3^r
x^{8 - r} = x⁵ ⇒ 8 - r = 5
∴ r = 3
∴ x⁵ का गुणांक = ⁸C₃ . 3³ = ⁸C₃ . 27
= \(\frac{8 \times 7 \times 6}{3 \times 2 \times 1}\) × 27
= 56 × 27 = 1512

प्रश्न 2.
(a - 2b)¹² में a⁵b⁷ का
हल:
हम जानते हैं कि व्यापक पद T_{r + 1} = ⁿC_r . a^{n - r} . b^r
∴ (a - 2b)¹² का व्यापक पद = ¹²C_r . a^{12 - r} . (- 2b)^r
= ¹²C_r . a^{12 - r} (- 1)^r . 2^r b^r
यहाँ b^r = b⁷ ∴ r = 7
∴ व्यापक पद = ¹²C₇ . a^{12 - 7} (- 1)⁷ . 2⁷ b⁷
= ¹²C₇ . a⁵b⁷ . (- 1) . 2⁷
∴ a⁵b⁷ का गुणांक = - ¹²C₇ . 2⁷
= - ¹²C₅ . 2⁷ [∵ ⁿC_r = ⁿC_{n - r}]
= - \(\frac{12 \times 11 \times 10 \times 9 \times 8}{5.4 .3 .2 .1}\) × 128
= - 101376
निम्नलिखित के प्रसार में व्यापक पद लिखिए:

प्रश्न 3.
(x² - y)⁶
हल:
व्यापक पद T_{r + 1} = ⁿC_r a^{n - r} b^r, 0 ≤ r ≤ n
∴ (x² - y)⁶ में व्यापक पद = ⁶C_r (x²)^{6 - r} (- y)^r
= ⁶C_r (x²)^{12 - 2r} (- y)^r
= (- 1)^{r 6}C_r, x^{12 - 2r} . y^r

प्रश्न 4.
(x² - yx)¹², x ≠ 0
हल:
∵ व्यापक पद T_{r + 1} = ⁿC_r a^{n - r} b^r, 0 ≤ r ≤ n
∴ (x² - yx)¹² में व्यापक पद = ¹²C_r (x²)^{6 - r} (- y)^r
= ¹²C_r x^{24 - 2r} (- 1)^r (y)^r (x)^r
= (- 1)^{r 12}C_r x^{24 - r} y^r

प्रश्न 5.
(x - 2y)¹² के प्रसार में चौथा पद ज्ञात कीजिए ।
हल:
(x - 2y)¹² के प्रसार में चौथा पद = T₄ = T_{3 + 1}
= ¹²C₃ (x)^{12 - 3} . (- 2y)³ [∵ T_{r + 1} = ⁿC_r . a^{n - r} . b^r]
= \(\frac{12 \times 11 \times 10}{3.2 .1}\) . (- 8) . x⁹ y³
= - 1760 x⁹ y³

प्रश्न 6.
\(\left(9 x-\frac{1}{3 \sqrt{x}}\right)^{18}\) के प्रसार में 13वाँ पद ज्ञात कीजिए।
हल:

= ¹⁸C₁₂ (3²)⁶ (x)⁶ (- 1)¹² . (3)^{- 12} . (x)^-6
= ¹⁸C₁₂ (3¹²) (x⁶) (3)^{- 12} (x)^{- 6} ∵ (- 1)¹² = 1
= ¹⁸C₁₂ . 3^{12 - 12} . x^{6 - 6} = ¹⁸C₁₂ . 3⁰ . x⁰
= \(\frac{18 !}{12 !(18-12) !} = \frac{18 !}{12 ! 6 !}\) = \(\frac{18 \times 17 \times 16 \times 15 \times 14 \times 13}{6 \times 5 \times 4 \times 3 \times 2 \times 1}\)
= 18564

निम्नलिखित प्रसारों के मध्य पद ज्ञात कीजिए:

प्रश्न 7.
\(\left(3-\frac{x^3}{6}\right)^7\)
हल:
दी गई संख्या \(\left(3-\frac{x^3}{6}\right)^7\) घात 7 है जो कि विषम प्राकृत संख्या है। ∴ मध्य पद T_{\(\frac{7+1}{2}\)} तथा T_{\(\frac{7+3}{2}\)} अर्थात् T₄ व T₅ होंगे।

प्रश्न 8.
\(\left(\frac{x}{3}+9 y\right)^{10}\)
हल:
संख्या \(\left(\frac{x}{3}+9 y\right)^{10}\) की घात 10 है जो कि एक सम प्राकृत संख्या है।

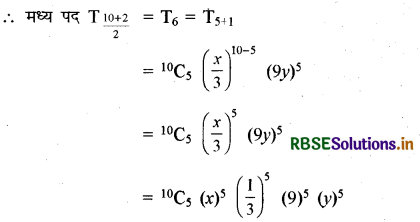
= ¹⁰C₅ (3)⁵ (3²)⁵ x⁵ y⁵
= ¹⁰C₅ (3)⁵ (3)¹⁰ x⁵ y⁵
= ¹⁰C₅ 3⁵ x⁵ y⁵
= (252) (243) x⁵ y⁵
= 61236 x⁵ y⁵

प्रश्न 9.
(1 + a)^{m + n} के प्रसार में सिद्ध कीजिए कि a^m तथा aⁿ के गुणांक बराबर हैं।
हल:
द्विपद प्रमेय के आधार पर हम जानते हैं कि
(1 + a)^m+n = [^m+nC_o + ^m+nC₁ a¹ + ^{m + n}C₂ a² + ................. + ^m+nC_r a^r + ...................... + ^m+nC_m+n a^m+n]
अतः a^m का गुणांक = ^m+nC_m = \(\frac{(m+n) !}{m ! n !}\)
तथा aⁿ का गुणांक = ^m+nC_n = \(\frac{(m+n) !}{m ! n !}\)
अर्थात् ^m+nC_m = ^m+nC_n
अतः यह कहा जा सकता है कि a^m तथा aⁿ के गुणांक समान हैं।

प्रश्न 10.
यदि (x + 1)ⁿ के प्रसार में (r - 1)^वाँ, r^वाँ और (r + 1)^वाँ पदों के गुणांकों में 1:3:5 का अनुपात हो, तो n तथा का मान ज्ञात कीजिए।
हल:
(x + 1)ⁿ के प्रसार में व्यापक पद T_{r + 1} = ⁿC_r . x^{n - r}
∴ प्रश्नानुसार (r - 1) वें पद का गुणांक = ⁿC_{r - 2}
rवें पद का गुणांक = ⁿC_{r - 1}
तथा (r + 1) वें पद का गुणांक = ⁿC_r
अब प्रश्नानुसार ⁿC_{r - 2} : ⁿC_{r - 1} : ⁿC_r = 1 : 3 : 5

⇒ r = 3
r का मान समीकरण n - 4r = - 5 में रखने पर
⇒ n - 4 × 3 = - 5
या n = - 5 + 12 = 7
अत: n = 7 तथा r = 3

प्रश्न 11.
सिद्ध कीजिए कि (1 + x)²ⁿ के प्रसार में " का गुणांक, (1 + x)^{2n - 1} के प्रसार में x²ⁿ के गुणांक का दुगुना होता है।
हल:
द्विपद प्रमेय के आधार पर हम लिख सकते हैं कि
(1 + x)²ⁿ = ²ⁿC_o + ²ⁿC₁ x¹ + ²ⁿC₂ x² + ......................... + ²ⁿC_n xⁿ
तथा (1 + x)^{2n - 1} = ^{2n - 1}C₀ + ^{2n - 1}C₁ x¹ + ^{2n - 1}C₂ x² + ...................... + ^{2n - 1}C_n xⁿ
(1 + x)²ⁿ में xⁿ का गुणांक = ²ⁿC_n
तथा (1 + x)^{2n - 1} में xⁿ का गुणांक = ^{2n - 1}C_n
सिद्ध करना है कि ²ⁿC_n = 2 (^{2n - 1}C_n)

प्रश्न 12.
m का धनात्मक मान ज्ञात कीजिए जिसके लिए (1 + x)^m के प्रसार में x² का गुणांक 6 हो ।
हल:
हम जानते हैं कि
(1 + x)^m = ^mC_o + ^mC₁ x² + ^mC₂ x² + ......... + ^mC_m x^m
इस प्रसार में x² का गुणांक ^mC₂ होगा जो कि प्रश्नानुसार 6 के बराबर है।
∴ ^mC₂ = 6
⇒ \(\frac{m !}{2 !(m-2) !}\) = 6
या \(\frac{m(m-1)(m-2) !}{2 !(m-2) !}\) = 6
या m (m - 1) = 2 × 6
या m² - m = 12
या m² - m - 12 = 0
या m² - 4m + 3m - 12 = 0
या m (m - 4) + 3 (m - 4) = 0
या (m - 4 ) (m + 3 ) = 0.
या m - 4 = 0
या m + 3 = 0
या m = 4 या m = - 3
नकारात्मक मान को उपेक्षणीय मानने पर m = 4