RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 8 Binomial Theorem Ex 8.2

Question 1
x⁵ in (x + 3)⁸
Answer:
Let x⁵ occurs in (r + 1)^th term in the expansion of (x + 3)⁸.
Then, (r + 1)^th term in expansion of (x + 3)⁸
T_{r + 1} = ⁸C_rx^{8 - r} (3)^r.
∵ Here power of x is 5, so x^{8 - r} = x⁵
Thus, x⁸ - x⁵ (given)
Comparing powers
8 - r = 5
∴ r = 8 - 5 = 3
Then, (r + 1)^th term, T_{r + 1} = ⁸C₃ x⁵ 3³
Thus, coefficient of x⁵ = ⁸C₃ 3³

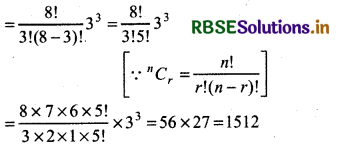
Thus, coefficient of x⁵ in the expansion of
(x + 3)⁸ = 1512

Question 2.
a⁵b⁷ in (a - 2b)¹².
Answer:
Let in expansion of (a - 2b)¹² coefficient of (r + 1)^th term will be a⁵b⁷
Then in expansion of (a - 2b)¹², (r + 1)^th term.
T_{r + 1} = ¹²C_r (a)^{12 - r} (- 2b)^r
We have, a^{12 - r} (- 2b)^r = a⁵b⁷
Comparing power of a on both sides
12 - r = 5
or r = 7
Then (r + 1)^th term., T_{r + 1} = ¹²C₇ a^{12 - 7}(- 2b)⁷
= \(\frac{12 !}{7 !(12-7) !}\) a⁵(- 2)⁷ b⁷
= \(\frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 !}{7 ! \times 5 \times 4 \times 3 \times 2 \times 1}\) × a⁵ (- 2)⁷ b⁷
= 792 (- 128)a⁵ b⁷
= - 101376 a⁵ b⁷
Thus, coefficient of a⁵b⁷ in (a - 2b)¹² = - 101376

Write the general term in the expansion of

Question 3.
(x² - y)⁶
Answer:
General term in expansion of (x² - y)⁶
T_{r + 1} = ⁶C_r (x²)^{6 - r} (- y)^r [∵ T_{r + 1} = ⁿC_r x^{n - r} a⁴]
= ⁶C_r x^{12 - 2r} (- 1)^r y^r
= ⁶C_r (- 1)^r x^{12 - 2r} y^r
Thus, general term in expansion of (x² - y)⁶
= ⁶C_r x^{12 - 2r} y^r

Question 4.
(x² - yx)¹², x ≠ 0
Answer:
General term in expansion of (x² - yx)¹²
T_{r + 1} = ¹²C_r (x²)^{12 - r} (- yx)^r [∵ T_{r + 1} = ⁿC_r x^{n - r} a⁴]
= ¹²C_r x^{24 - 2r} (- 1)^r y^r x^r
= ¹²C_r x^{24 - 2r + r} (- 1)^r y^r
= ¹²C_r (- 1)^r x^{24 - r} y^r
Thus, general term in expansion of (x² - yx)¹²
= ¹²C_r (- 1)^r x^{24 - r} y^r

Question 5.
Find the fourth term ¡n the expansion of (x - 2y)¹²
Answer:
4^th term in expansion of (x - 2y)¹²
T₄ or T_{3 + 1} = ¹²C₃ x^{12 - 3} (- 2y)³ [∵ T_{r + 1} = ⁿC_r x^{n - r} a⁴]

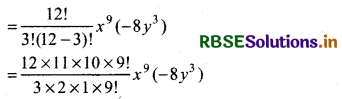
= 220 (- 8)x⁹ y³ = - 1760 x⁹ y³
Thus, 4^th term in expansion (x - 2y)¹²
= - 1760 x⁹ y³

Question 6.
Find the 13^th term in the expansion of
\(\left(9 x-\frac{1}{3 \sqrt{x}}\right)^{18}\), x ≠ 0.
Answer:

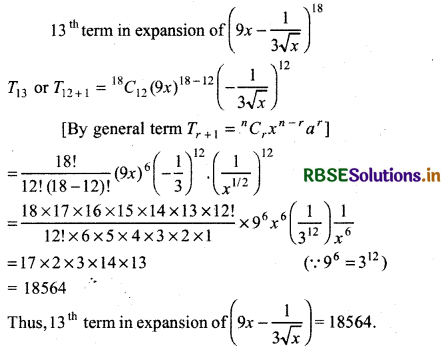
Find the middle terms in the expansions of

Question 7.
\(\left(3-\frac{x^3}{6}\right)^7\).
Answer:

Question 8.
\(\left(\frac{x}{3}+9 y\right)^{10}\)
Answer:

Question 9.
In the expansion of (1 + a)^{m + n}, prove that coefficients of a^m and aⁿ are equal.
Answer:
By general term T_{r + 1} = ⁿC_rx^{n - r}a^r
(r +1) th term in the expansion of
(1 + a)^{m + n} = ^{m + n}C_ra^r
Putting r = m, coeff. of x^m = ^{m + n}C_m
Putting r = n, coeff. of x^m = ^{m + n}C_n
= ^{m + n}C_{m + n - n} = ^{m + n}C_m
Thus, coeff. of x^m = coff. of xⁿ
[ⁿC_r = ⁿC_{n - r}]
Hence Proved

Question 10.
The coefficient of the (r - 1)^th, r^th and (r + 1)^th terms in the expansion of (x + 1)ⁿ are in the ratio 1 : 3 : 5. Find n and r.
Answer:
(x + 1)ⁿ = ⁿC₀ + ⁿC₁x^{n - 1} + ⁿC₂x^{n - 2} + ..... + ⁿC_rx^{n - r} + .......... ⁿC_n
(r - 1) th term = T_{(r - 2) + 1}
= T_{r - 1} = ⁿC_{r - 2} x^{n - (r - 2)}
= ⁿC_{r - 2} x^{n - r + 2}
r th term = T_{(r - 1) + 1}
= ⁿC_{r - 1} x^{n - 1(r - 1)}
= ⁿC_{r - 1} x^{n - r + 1}
(r + 1) th term = ⁿC_r x^{n - r} and coefficient of the r^th, (r - 1)^th and (r + 1)^th terms respectively will be ⁿC_{r - 2}, ⁿC_{r - 1} and ⁿC_r.
Thus, ⁿC_{r - 2} : ⁿC_{r - 1} : ⁿC_r = 1 : 3 : 5

or 3r - 3 = n - r + 2
or 3r + r = n + 2 + 3
or 4r = n + 5
or n = 4r - 5

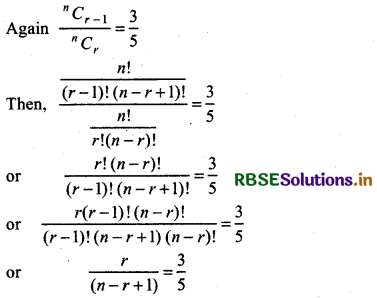
or 5r = 3n - 3r + 3
or 3n = 5r + 3r - 3
3n = 8r - 3
From equation (1) and (2)
3 × (4r - 5) = 8r - 3
or 12r - 15 = 8r - 3
or 12r - 8r = 15 - 3
or. 4r = 12
∴ r = 3
Putting value of r in equation (1)
n = 4r - 5
or n = 4 × 3 - 5
or n = 12 - 5
∴ n = 7
Thus, n = 7, r = 3

Question 11.
Prove that the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is twice the coefficient of xⁿ in the expansion of (1 + x)^{2n - 1}.
Answer:
(r + 1)^th term in the expansion of (1 + x)²ⁿ
Putting r = n, coefficient of xⁿ = ²ⁿC_n
Similarly, coefficient of xⁿ in expansion of (1 - x)^{2n - 1}
= ^{2n - 1}C_n

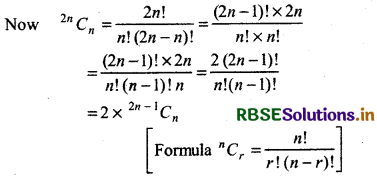
Thus in expansion of (1 + x)²ⁿ coefficient of xⁿ
= 2 × coeff. of xⁿ in expansion of (1 + x)^{2n - 1}
Hence Proved

Question 12.
Find a positive value of m for which the coefficient of x² in the expansion (1 + x)^m is 6.
Answer:
By Binomial theorem.
(1 + x)^m = ^mC₀ +^mC₁x + ^mC₂x² + .....
Then, coefficient of of x² in expansion of (1 + x)ⁿ = ^mC₂
But given that coeff. of x² = 6
Thus, ^mc₂ = 6

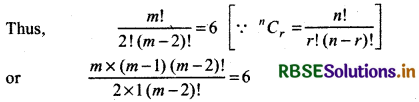
or m(m - 1) = 2 × 6
or m² - m - 12 = 0
or m² - (4 - 3)m - 12 = 0
or m² - 4m + 3m - 12 = 0
or m(m - 4) + 3(m - 4) = 0
or (m- 4) (m + 3) = 0
∴ m = 4
m = - 3
But value of m is not negative. Thus, m = 4