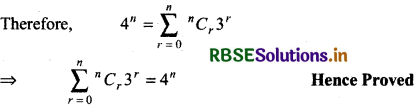RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 8 Binomial Theorem Ex 8.1

Expand each of the expressions in Exercise 1 to 5.

Question 1.
(1 - 2x)5
Answer:
(1 - 2x)5 = [1 + (- 2x)]5
Using binomial theorem, 
(1 - 2x)5 = 5C0 (1)5 (- 2x)0 + 5C1 (1)4 (- 2x)1 + 5C2(1)3 (- 2x) + 5C3(1)2 (- 2x)3 + 5C4(1)1 (- 2x)4 + 5C5 (1)0 (- 2x)5
= 1 + 5(- 2x) + 10(- 2x)2 + 10 (- 2x)3 + 5(- 2x)4 + (- 2x)5
= 1 - 10x + 40x2 - 80x3 + 80x4 - 32x5
Thus, (1 - 2x)5 = 1 - 10x + 40x2 - 80x3 + 80x4 - 32x5

RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 2.
\(\left(\frac{2}{x}-\frac{x}{2}\right)^5\)
Answer:
RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 1

Question 3.
(2x - 3)6
Answer:
(2x - 3)6 = [2x + (3)]6
Using binomial theorem,
(2x - 3)6 = 6C0 (2x)6 (- 3)0 + 6C1 (2x)5 (- 3) + 6C2 (2x)4 (- 3)2 + 6C3(2x)3 (- 3)3 + 6C4(2x)2 (- 3)4 + 6C5(2x) (- 3)5 + 6C6(2x)0 (- 3)6
= 1 × 64x6 × 1 + 6 × 32x5 × (- 3) + 15 × 16x4 × 9 + 20 × 8x3 × (- 27) + 15 × 4x2 × 81 + 6 × 2x (- 243) + 1 × 1 × 729
= 64x6 - 576x5 + 2160x4 - 4320x3 + 4860x2 - 2916x + 729
Thus, (2x - 3)6 = 64x6 - 576x5 + 2160x4 - 4320x3 + 4860x2 - 2916x + 729

Question 4.
\(\left(\frac{x}{3}+\frac{1}{x}\right)^5\)
Answer:
By Binomial theorem,
RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 2

RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 5.
\(\left(x+\frac{1}{x}\right)^6\)
Answer:
Using Binomial theorem,
RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 3

Question 6.
(96)3
Answer:
96 = 100 - 4
Thus, (96)3 = (100 - 4)3 = [100 + (- 4)]3
Using binomial theorem,
(96)3 =(100 + (- 4))3
= 33C0(100)3(- 4)0 + 3C1 (100)2 (- 4)1 + 3C2 (100) (- 4)2 + 3C3(100)0 (- 4)3
= 1 × 100000 × 1 + 3 × 10000 × (- 4) + 3 × 100 × 16 + 1 × 1 × (- 64)
= 10000Q - 120000 + 4800 - 64
= 1004800 - 120064 = 884736
Thus, (96)3 = 884736

RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 7.
(102)5
Answer:
102 = 100 + 2
Thus, (102)5 = (100 + 2)5
Using binomial theorem.
(102) = (100 + 2)5
= 5C0 (100)5 (2)0 + 5C1 (100)4 (2)1 + 5C2 (100)3 (2)2 + 5C3 (100)2 (2)3 + 5C4 (100)(2)4 + 5C5(100)025
= 1 × 10000000000 × 1 + 5 × 100000000 × 2 + 10 × 1000000 × 4 + 10 × 10000 × 8 + 5 × 100 × 10 + 1 × 1 × 32
= 10000000000 + 1000000000 + 40000000 + 800000 + 8000 + 32
= 11040808032
Thus, (102)5 = 11040808032

Question 9.
(99)5
Answer:
99 = (100 - 1)
Thus, (99)5 = (100 - 1)5 = [100 + (- 1)]5
Using binomial theorem,
995 = 5C0 (100)5 (- 1)0 + 5C1 (100)4 (- 1)1 + 5C2 (100)3 (- 1)2 + 5C3 (100)2 (- 1)3 + 5C4 (100) (- 1)4 + 5C5 (100)0 (- 1)5
= 1 × 10000000000 × 1 + 5 × 100000000 × (- 1) + 10 × 1000000 × 1 + 10 × 10000 × (- 1) + 5 × 100 × 1 + 1 × 1 × (- 1)
= 10000000000 - 500000000 + 10000000 - 100000 + 500 - 1
= 10010000500 - 500100001
= 9509900499
Thus, (99)5 = 9509900499

Question 10.
Using binomial theorem, find which number is larger (1.1)10000 or 1000.
Answer:
(1.1)10000 = (1 + 0.1)10000
= 10000C0 (1)10000 (0.1)0 + 10000C1 (1)9999 (0.1)1 + ................
= 1 × 1 × 1 + 10000 × 1 × 01 + .......
= 1 + 1000 + ........ other positive numbers
= 1001 + .... other positive numbers
Thus, (1.1)10000 = 1001 + .... other positive numbers
But 1001 > 1000
Then. (1 .1)10000 >1000.
(1.1)10000 is greater

RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 11.
Find (a + b)4 - (a - b)4
Hence, evaluate (√3 + √2)4 - (√3 - √2)4.
Answer:
RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 4

RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 12.
Find (x + 1)6 + (x - 1)6. Hence, or otherwise, evaluate (√2 + 1)6 + (√2 - 1)6.
Answer:
By Binomial theorem.
(x + 1)6 = 6C0 x6 10 + 6C1 x5 (1)1 + 6C2 x4 (1)2 + 6C3 x3 (1)1 + 6C4 x2 (1)4 + 6C5 x1 (1)5 + 6C6 x0 (1)6
= 6C0 x6 + 6C1x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6
(x + 1)6 = x6 + 6x5 + 15x4 + 20x3 + 15x2 + 6x + 1 ....... (1)
Similarly,
(x - 1)6 = x6 - 6x5 + 15x4 - 20x3 + 15x2 - 6x + 1 ...... (2)
Adding equation (1) and (2)
(x + 1)6 + (x - 1)6 = 2(x6 + 15x4 + 15x2 + 1)
Putting x = √2 in above equation,
(√ 2 + 1)6 + (√2 - 1)6
= 2[(√ 2)6 + 15(√2)4 + 15(√2)2 + 1]
= 2[23 + 15(2)2 + 15(2) + 1]
= 2[8 + 60 + 30 + 1]
= 198
Thus, (√2 + 1)6 + (√2 - 10)6 = 198

Question 13.
Show that 9n + 1 - 8n - 9, is divisible by 64. whenever n is a positive integer.
Answer:
By binomial theorem,
RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 5
We see that In R.H.S. one factor of 64. Thus R.H.S. is divisible by 64 then 9n + 1 - 8n - 9 will also be divisible by 64.

RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 14.
Prove that \(\sum_{i=0}^n\) 3r . nCr = 4n
Answer:
By Binomial theorem,
(1 + x)n = nC0 x0 + nC1 x + nC2 x2 + nC3 x3 + nC4 x4 + ........ + nCn xn
Putting x = 3 in both sides,
(1 + 3)n = nC0 30 + nC1 31 + nC2 32 + nC3 33 + nC4 34 + ......... + nCn 3n
RBSE Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1 6

Bhagya
Last Updated on Nov. 7, 2023, 9:47 a.m.
Published Nov. 6, 2023