RBSE Solutions for Class 11 Maths Chapter 7 क्रमचय और संचयं विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 7 क्रमचय और संचयं विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 7 क्रमचय और संचयं विविध प्रश्नावली

प्रश्न 1.
DAUGHTER शब्द के अक्षरों से कितने अर्थपूर्ण या अर्थहीन शब्दों की रचना की जा सकती है, जबकि प्रत्येक शब्द में 2 स्वर तथा 3 व्यंजन हों ?
हल:
DAUGHTER शब्द में कुल 8 अक्षर हैं जिनमें 5 व्यंजन तथा 3 स्वर हैं। 3 स्वरों में से 2 स्वर चुनने के प्रकार
= ³C₂ = ³C₁ = 3
इसी प्रकार 5 व्यंजनों में से 3 व्यंजन चुनने के प्रकार
= ⁵C₃ = ⁵C₂ = \(\frac{5.4}{2.1}\) = 10 [:: ⁿC_r = ²C_n-r]
इस तरहं 2 स्वर तथा 3 व्यंजन चुनने के प्रकार = 3 × 10 = 30
चूँकि प्रत्येक संचय में 5 अक्षर हैं अतः उनके क्रमचयों की संख्या = 5!
= 5 × 4 × 3 × 2 × 1 = 120
अतः DAUGHTER शब्द के 2 स्वर और 3 व्यंजन लेकर बने शब्दों की संख्या
= 30 × 120 = 3600

प्रश्न 2.
EQUATION शब्द के अक्षरों से कितने, अर्थपूर्ण या अर्थहीन, शब्दों की रचना की जा सकती है, जबकि स्वर तथा व्यंजक एक साथ रहते हैं ?
हल:
EQUATION शब्द में 8 अक्षर हैं जिनमें 5 स्वर तथा 3 व्यंजन हैं। अत: स्वर अक्षरों का क्रमचय
= = 5!
= 5 × 4 × 3 × 2 × 1 = 120
तथा व्यंजन अक्षरों का क्रमचय = 3!
= 3 × 2 × 1 = 6
स्वरों को एक साथ रखने पर EUAIO तथा व्यंजनों को एक साथ रखने पर QTN दो समूह बनते हैं। स्वरों तथा व्यंजनों को 2 प्रकार से लिखा जा सकता है— पहले स्वर लें या पहले व्यंजन लें। अत: EQUATION शब्द के अक्षरों से बनने वाले अर्थपूर्ण या अर्थहीन शब्द जबकि स्वर तथा व्यंजन एक साथ लें
= 2 × 5! × 3!
= 2 × 120 × 6
= 1440

प्रश्न 3.
9 लड़के और 4 लड़कियों से 7 सदस्यों की एक समिति बनानी है । यह कितने प्रकार से किया जा सकता है, जबकि समिति में,
(i) तथ्यतः 3 लड़कियाँ हैं ?
(ii) न्यूनतम 3 लड़कियाँ हैं ?
(iii) अधिकतम 3 लड़कियाँ हैं ।
हल:
लड़कों की संख्या = 9
तथा लड़कियों की संख्या = 4
(i) तथ्यतः लड़कियाँ होने के 7 सदस्यों की समिति में 4 लड़के और चुनने पड़ेंगे अर्थात् समितियों की संख्या
= ⁴C₃ × ⁹C₄ = ⁴C₁ × ⁹C₅ [∵ ⁿC_r = ⁿC_n-r]
= 4 × \(\frac{9 !}{5 ! 4 !}\)
= 4 × \(\frac{9 \times 8 \times 7 \times 6 \times 5 !}{5 ! 4 !}\)
= \(\frac{4 \times 9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1}\)
= 504

(ii) समिति में कम से कम 3 लड़कियाँ होने पर (a) या तो 3 लड़कियाँ व 4 लड़के हों या (b) 4 लड़कियाँ व 3 लड़के हों । अतः इन समितियों के प्रकार (a) के अनुसार
= ⁴C₃ × ⁹C₄ = ⁴C₁ × ⁹C₅
= 4 × \(\frac{9 !}{5 ! 4 !}\)
= 504

तथा इन समितियों के प्रकार (b) के अनुसार
= ⁴C₄ × ⁴C₃
= 1 × ⁹C₆ = ⁹C₆
= \(\frac{9 !}{6 ! 3 !}\) = 84
अतः समितियों में चयन के प्रकार = 504 + 84 = 588

(iii) यदि समिति में अधिकतम 3 लड़कियाँ लेनी हैं तो (a) कोई लड़की नहीं तथा 7 लड़के (b) 1 लड़की तथा 6 लड़के (c) 2 लड़की तथा 5 लड़के (d) 3 लड़की तथा 4 लड़के होने चाहिए।
∴ (a) यदि समिति में कोई लड़की नहीं एवं 7 लड़के हों तो समिति बनाने के प्रकार
= ⁴C₀ × ⁹C₇
= 1 × ⁹C₂
= 1 × \(\frac{9 \times 8}{2 \times 1}\) = 36

(b) यदि समिति में 1 लड़की तथा 6 लड़के हों तो समिति बनाने के प्रकार
= ⁴C₁ × ⁹C₆ = ⁴C₁ × ⁹C₃
= \(\frac{4}{1} \times \frac{9.8 .7}{3 \times 2 \times 1}\) = 2 × 3 × 8 × 7
= 336

(c) यदि समिति में 2 लड़की तथा 5 लड़के हों तो समिति बनाने के प्रकार
= ⁴C₂ × ⁹C₅ = ⁴C₂ × ⁹C₄
= \(\frac{4 \times 3}{2 \times 1} \times \frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1}\)
= 756

(d) यदि समिति में 3 लड़की तथा 4 लड़के हों तो समिति बनाने के प्रकार
= ⁴C₃ × ⁹C₄ = ⁴C₁ × ⁹C₄
= \(\frac{4}{1} \times \frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1}\) = 504
∴ कुल प्रकार = 36 +336 + 756 + 504
= 1632

प्रश्न 4.
यदि शब्द EXAMINATION के सभी अक्षरों से बने विभिन्न क्रमचयों को शब्दकोश की तरह सूचीबद्ध किया जाता है, तो E. से प्रारम्भ होने वाले प्रथम शब्द से पूर्व कितने शब्द हैं ?
हल:
शब्द EXAMINATION में कुल 11 अक्षर हैं । A से प्रारम्भ होने वाले शब्दों में 1-2, N - 2 तथा शेष अन्य अक्षर हैं । अतः ऐसे

शब्दों की संख्या = \(\frac{10 !}{2 ! 2 !}\)
= \(\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 2 \times 1}\)
= \(\frac{3628800}{4}\) = 907200
अतः E से प्रारम्भ होने वाले शब्दों से पहले शब्दकोश की तरह सूचीबद्ध करने पर क्रमचयों की संख्या = 907200

प्रश्न 5.
0, 1, 3, 5, 7 तथा 9 अंकों से, 10 से विभाजित होने वाली और बिना पुनरावृत्ति किए कितनी 6 अंकीय संख्याएँ बनाई जा सकती हैं ?
हल:
6 अंकीय संख्या बनाने के लिए दिए अंक 0, 1, 3, 5, 7 तथा 10 हैं। 10 से विभाजित होने वाली 6 अंकीय संख्याएँ वे होंगी जिनमें इकाई का अंक शून्य हो । अर्थात् अब हमें 6 अंकीय संख्या . बनाने के लिए शेष 5 स्थान और भरने हैं । अतः 5 स्थानों को
भरने का क्रमचय = 5!
= 5 × 4 × 3 × 2 × 1
= 120
अतः 6 अंकीय 10 से विभाजित होने वाली कुल संख्या = 120

प्रश्न 6.
अंग्रेजी वर्णमाला में 5 स्वर तथा 21 व्यंजन हैं। इस वर्णमाला से 2 भिन्न स्वरों और 2 भिन्न व्यंजनों वाले कितने शब्दों की रचना की जा सकती है ?
हल:
5 स्वरों में से दो भिन्न स्वर चुनने के प्रकार = ⁵C₂
तथा 21 व्यंजनों में से 2 भिन्न व्यंजन चुनने के प्रकार = ²¹C₂
अतः 2 स्वरों तथा 2 व्यंजनों का चयन करने के कुल प्रकार = ⁵C2 × ²¹C₂
2 स्वरों तथा 2 व्यंजनों का क्रमचय = 4!
∴ 2 स्वर तथा 2 व्यंजनों से बनने वाले कुल शब्दों की संख्या
= ⁵C₂ × ²¹C₂ × 4!
= \(\frac{5 \times 4}{2 \times 1} \times \frac{21 \times 20}{2 \times 1}\) × 4 × 3 × 2 × 1
= 10 × 210 × 24
= 50400

प्रश्न 7.
किसी परीक्षा के एक प्रश्नपत्र में 12 प्रश्न हैं जो क्रमश: 5 तथा 7 प्रश्नों वाले दो खण्डों में विभक्त हैं अर्थात् खण्ड I और खण्ड II. एक विद्यार्थी को प्रत्येक खण्ड से न्यूनतम 3 प्रश्नों का चयन करते हुए कुल 8 प्रश्नों को हल करना है । एक विद्यार्थी कितने प्रकार से प्रश्नों का चयन कर सकता है ?
हल:
एक विद्यार्थी को कुल 8 प्रश्नों का चयन इस प्रकार करना है कि प्रत्येक खण्ड से कम से कम 3 प्रश्न चुने जाएँ । जबकि प्रथम खण्ड में 5 प्रश्न तथा द्वितीय खण्ड में प्रश्नों की संख्या 7 है । यह
निम्नानुसार चयन हो सकता है-

अब यदि विद्यार्थी (i) चयन करता है तो 8 प्रश्नों को चुनने का प्रकार = ⁵C₃ × ⁷C₅
यदि विद्यार्थी (ii) चयन करता है तो 8 प्रश्नों को चुनने का प्रकार = ⁵C₄ × ⁷C₄
तथा यदि विद्यार्थी (iii) चयन करता है तो 8 प्रश्नों को चुनने का प्रकार = ⁵C₅ × ⁷C₃
इस प्रकार 8 प्रश्नों के चयन के कुल प्रकार
= (⁵C₃ × ⁷C₅) + (⁵C₄ × ⁷C₄) + (⁵C₅ × ⁷C₃)
= (10 × 21) + (5 × 35) + (1 × 35)
= 210+ 175 + 35
= 420

प्रश्न 8.
52 पत्तों की एक गड्डी में से 5 पत्तों के संचय की संख्या निर्धारित कीजिए, यदि 5 पत्तों के प्रत्येक चयन (संचय) में तथ्यतः एक बादशाह है ।
हल:
52 पत्तों की एक ताश की गड्डी में 4 बादशाह तथा 48 अन्य प्रकार के पत्ते होते हैं । हमें 5 पत्तों के प्रत्येक चयन में एक बादशाह तथा 4 अन्य ताशों का चयन करना है । यह चयन का प्रकार
= ⁴C₁ × ⁴⁸C₄
= \(\frac{4 !}{1 ! 3 !} \times \frac{48 !}{4 ! 44 !}\)
= \(\frac{4 !}{1 ! 3 !} \times \frac{48 !}{4 ! 44 !}\)
= 778320

प्रश्न 9.
5 पुरुषों और 4 महिलाओं को एक पंक्ति में इस प्रकार बैठाया जाता है कि महिलाएँ सम स्थानों पर बैठती हैं । इस प्रकार के कितने विन्यास सम्भव हैं ?
हल:
4 महिलाओं का 4 सम स्थानों पर बैठाने का विन्यास
= 4! = 4 × 3 × 2 × 1
= 24
तथा 5 पुरुषों को 5 विषम स्थानों पर बैठाने का प्रकार
= 5 ! = 5 × 4 × 3 × 2 × 1
= 120

अतः 4 महिलाओं को सम स्थानों पर तथा 5 पुरुषों को विषम स्थानों पर बैठाने के विन्यास
= 4! × 5!
= 24 × 120
= 2880

प्रश्न 10.
25 विद्यार्थियों की एक कक्षा से, 10 का चयन एक भ्रमण दल लिए किया जाता है । 3 विद्यार्थी ऐसे हैं, जिन्होंने यह निर्णय लिया है कि या तो वे तीनों दल में शामिल होंगे या उनमें से कोई भी दल में शामिल नहीं होगा। भ्रमण दल का चयन कितने प्रकार से किया जा सकता है?
हल:
25 विद्यार्थियों की कक्षा में से 10 विद्यार्थियों का चयन भ्रमण दल में किया जाता है । लेकिन 10 विद्यार्थियों में से 3 ने यह निर्णय लिया है कि
(i) या तो वे भ्रमण दल में शामिल होंगे। ऐसी स्थिति में भ्रमण दल का चयन करने के प्रकार
= ²²C₇
(ii) या वे भ्रमण दल में शामिल नहीं होंगे। ऐसी स्थिति में भ्रमण दल का चयन करने के प्रकार
= ²²C₁₀
अतः दोनों स्थितियों में भ्रमण दल के चयन के प्रकार
= ²²C₇ + ²²C₁₀

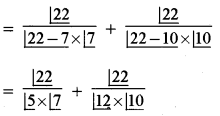
= 170544 + 656646
= 817190

प्रश्न 11.
ASSASSINATION शब्द के अक्षरों के कितने विन्यास बनाए जा सकते हैं, जबकि सभी 'S' एक साथ रहें?
हल:
शब्द ASSASSINATION में कुल 13 अक्षर हैं जिसमें A- तीन, S - चार, I-दो, N - दो तथा T - 1 है | दी गई शर्त के अनुसार चारों S एक साथ रहें तो इनको एक अक्षर मानना पड़ेगा । अतः अब कुल अक्षर = 10
इसमें A-3, I-2 तथा N-2 हैं । अतः इस शब्द के अक्षरों का 'विन्यास जबकि चारों S एक साथ हों-
= \(\frac{10 !}{3 ! 2 ! 2 !}\)
= \(\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1 \times 2 \times 1 \times 2 \times 1}\)
= 151200