RBSE Solutions for Class 11 Maths Chapter 7 क्रमचय और संचयं Ex 7.4

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 7 क्रमचय और संचयं Ex 7.4 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 7 क्रमचय और संचयं Ex 7.4

प्रश्न 1.
यदि ⁿC₈ = ⁿC₂, तो ⁿC₂ ज्ञात कीजिए ।
हल:
प्रश्नानुसार ⁿC₈ = ⁿC₂
∴ 8 + 2 = n ∴ n = 10
[क्योंकि ⁿC_x = ⁿC_y ⇒ x + y = n]

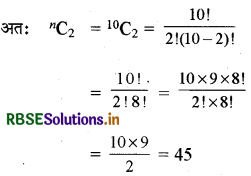
प्रश्न 2.
n का मानं निकालिए, यदि
(i) ²ⁿC₃: ⁿC₂ = 12 : 1
(ii) ²ⁿC₃: ⁿC₃ = 11 : 1
हल:
(i) प्रश्नानुसार
²ⁿC₃: ⁿC₂ = 12 : 1

या 2n - 1 = \(\frac{6 \times 6}{4}\) = 9
या 2n - 1 = 9
या 2n = 9 + 1 = 10
या n = 5

(ii) प्रश्नानुसार ²ⁿC₃: ⁿC₃ = 11 : 1

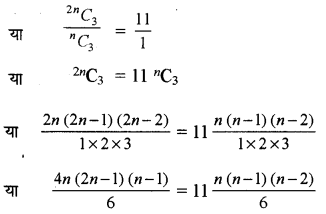
या 4 (2n - 1) = 11 (n – 2)
या 8n – 4 = 11n - 22
या 8n – 11n= – 22 + 4
या - 3n = - 18
या n = 6

प्रश्न 3.
किसी वृत्त पर स्थित 21 बिन्दुओं से होकर जाने वाली कितनी जीवाएँ खींची जा सकती हैं ?
हल:
एक वृत्त के किन्हीं दो बिन्दुओं को मिलाने पर ही एक जीवा प्राप्त होती है । अत: 21 बिन्दुओं से एक जीवा ²¹C₂ प्रकार से खींची जा सकती है। अर्थात्
²¹C₂ = \(\frac{21 !}{2 ! 19 !}=\frac{21 \times 20 \times 19 !}{2 ! \times 19 !}=\frac{21 \times 20}{2}\)
= 210
अर्थात् खींची गई जीवाओं की संख्या = 210

प्रश्न 4.
5 लड़के और 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमें बनाने के कितने तरीके हैं ?
हल:
5 लड़कों में से 3 लड़के चुनने के प्रकार = ⁵C₃
= \(\frac{5 !}{3 ! 2 !}=\frac{5 \times 4}{2}\) = 10
इसी प्रकार 4 लड़कियों में से 3 लड़कियाँ चुनने के प्रकार = ⁴C₃
= \(\frac{4 !}{3 ! 1 !}\) = 4
अतः 5 लड़कों तथा 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमों की संख्या
= ⁵C₃ × ⁴C₃
= 10 × 4
= 40

प्रश्न 5.
6 लाल रंग की, 5 सफेद रंग की और 5 नीले रंग की गेंदों में से 9 गेंदों के चुनने के तरीकों की संख्या ज्ञात कीजिए, यदि प्रत्येक संग्रह में प्रत्येक रंग की 3 गेंदें हैं।
हल:
लाल रंग की 6 गेंदों में से 3 गेंदें चुनने के प्रकार = ⁶C₃
सफेद रंग की 5 गेंदों में से 3 गेंदें चुनने के प्रकार = ⁵C₃
नीले रंग की 5 गेंदों में से 3 गेंदें चुनने के प्रकार = ⁵C₃

इस प्रकार 6 लाल, 5 सफेद तथा 5 नीली गेंदों में से प्रत्येक रंग की 3 गेंदें चुनने के प्रकार
= ⁶C₃ × ⁵C₃ × ⁵C₃
= ⁶C₃ × ⁵C₃ × ⁵C₃ [∵ ⁿC_r = ⁿC_n-r]
= \(\frac{6.5 .4}{3.2 .1} \times \frac{5.4}{1.2} \times \frac{5.4}{1.2}\)
= 20 × 10 × 10 = 2000

प्रश्न 6.
52 पत्तों की एक गड्डी में से 5 पत्तों को लेकर बनने वाले संचयों की संख्या निर्धारित कीजिए, यदि प्रत्येक संचय में तथ्यतः एक इक्का है।
हल:
52 पत्तों की ताश की एक गड्डी में 4 इक्के तथा 48 अन्य ताश होते हैं। अब हम एक इक्का व 4 अन्य ताश चुन सकते हैं तथा यह ⁴C₁ × ⁴⁸C₄ प्रकार से किया जा सकता है
अर्थात् ⁴C₁ × ⁴⁸C₄

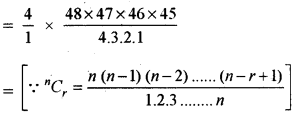
= 778320

प्रश्न 7.
17 खिलाड़ियों में से, जिनमें केवल 5 खिलाड़ी गेंदबाजी कर सकते हैं, एक क्रिकेट टीम के 11 खिलाड़ियों का चयन कितने प्रकार से किया जा सकता है, यदि प्रत्येक टीम में तथ्यतः 4 गेंदबाज हैं?
हल:
कुल खिलाड़ियों की संख्या = 17
कुल गेंदबाजों की संख्या = 5
उन खिलाड़ियों की संख्या जो गेंदबाजी नहीं कर सकते
= 17 - 5 = 12
एक क्रिकेट टीम 11 खिलाड़ियों की बनाने के लिए हम सात ऐसे खिलाड़ी चुन सकते हैं जो गेंदबाज नहीं हैं । अर्थात् 12 खिलाड़ियों में से ऐसे खिलाड़ियों = ¹²C₇
अतः कुल टीमों की संख्या = ⁵C₄ × ¹²C₇
= ⁵C₁ × ¹²C₅ [∵ ⁿC_r = ⁿC_n-r]
= \(\frac{5}{1} \times \frac{12 \times 11 \times 10 \times 9 \times 8}{5 \times 4 \times 3 \times 2 \times 1}\)
= 3960

प्रश्न 8.
एक थैली में 5 काली तथा 6 लाल गेंदें हैं। 2 काली तथा 3 लाल गेंदों के चयन के तरीकों की संख्या निर्धारित कीजिए ।
हल:
5 काली गेंदों में से 2 गेंदें चुनने के प्रकार = ⁵C₂
6 लाल गेंदों में से 3 गेंदें चुनने के प्रकार = ⁶C₃
अतः 5 काली तथा 6 लाल गेंदों में से 2 काली तथा 3 लाल गेंदें चुनने के कुल प्रकार
= ⁵C₂ × ⁶C₃
= \(\frac{5.4}{1.2} \times \frac{6.5 .4}{3.2 .1}\)
= 10 × 20 = 200

प्रश्न 9.
9 उपलब्ध पाठ्यक्रमों में से, एक विद्यार्थी 5 पाठ्यक्रमों का चयन कितने प्रकार से कर सकता है, यदि प्रत्येक विद्यार्थी के लिए 2 विशिष्ट पाठ्यक्रम अनिवार्य हैं ?
हल:
प्रत्येक विद्यार्थी के लिए 2 पाठ्यक्रम अनिवार्य हैं ।
∴ शेष पाठ्यक्रम = 9 - 2 = 7
7 पाठ्यक्रमों में से 3 पाठ्यक्रम चुनने के प्रकार = ⁷C₃
अतः 9 पाठ्यक्रमों में से 5 पाठ्यक्रम चुनने के प्रकार
= ⁷C₃ × ²C₂
= \(\frac{7.5 .4}{3.2 .1} \times \frac{1}{1}\)
= 35