RBSE Solutions for Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.4

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.4 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 7 Permutations and Combinations Ex 7.4

Question 1.
If ⁿC₈ = ⁿC₂, find ⁿC₂.
Answer:
ⁿC₈ = ⁿC₂
Then, ⁿC_{n - 8} = ⁿC₂ [∵ ⁿC_r = ⁿC_{n - r}]
Thus, n - 8 = 2
n = 2 + 8.
∴ n = 10
Then, ⁿC₂ = ¹⁰C₂

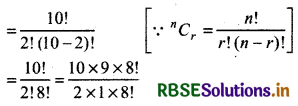
= 45
Thus, value of ⁿC₂ = ¹⁰C₂ = 45

Question 2.
Determine n, if
(i) ²ⁿC₃ : ⁿC₃ = 12 : 1
(ii) ²ⁿC₃ : ⁿC₃ = 11 : 1
Answer:
(i) ²ⁿC₃ : ⁿC₃ = 12 : 1

⇒ 4(2x - 1) = 12 (x - 2) ⇒ 8x - 4 = 12x - 24
⇒ 8x - 12x = 4 - 24 ⇒ - 4x = - 20 ⇒ 4x = 20
∴ n = 5
Thus, value of n = 5

(ii) ²ⁿC₃ : ⁿC₃ = 11 : 1

or 4(2n - 1) = 11(n - 2)
or 8n - 4 = 11n - 22
or 11n - 8n = 22 - 4
or 3n = 18
∴ n = 6
Thus, value of n = 6

Question 3.
How many chords can be drawn through 21 points on a circle?
Answer:
No. of points on a circle = 21
We know that through two points a chord can be drawn.
Thus, no. of chords will be equal to combination formed by taking 2 points out of 21 points.
No. of ways of taking 2 points out of 21 points.
= ²¹C₂

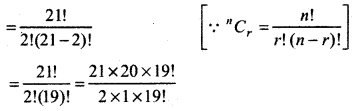
Thus, no of chords = 210.

Question 4.
In how many ways a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
Answer:
No. of ways to select 3 boys out of 5 boys = ⁵C₃
and no. of ways to select 3 girls out of 4 girls = ⁴C₃
Thus, no. of ways to select team

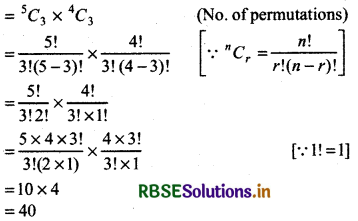
Thus, required no. of ways = 40

Question 5.
Find the number of ways of selecting 9 balls out of 6 red balls, 5 white balls and 50f blue colour balls. If each selection consists of 3 balls of each colour?
Answer:
We have total 9 balls have to select and 3 balls must be of each colour
Now we have to choose 3 balls out of 6 red balls, 3 out of 5 white balls and 3 baIls out of 5 blue balls.
No. of ways to select 3 balls out of 6 red balls = ⁶C₃
No. of ways to select 3 balls out of 5 white balls = ⁵C₃
No. of ways to select 3 balls out of 5 blue balls = ⁵C₃
Then no. of ways to select 9 balls
= ⁶C₃ × ⁵C₃ × ⁵C₃

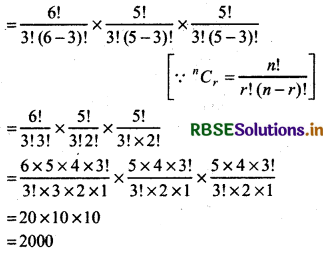
Thus, total no. of ways to select 9 balls, in which 3 balls of each colour exist = 2000.

Question 6.
Determine the number of 5 card combinations out of a deck of 52 cards if there ¡s exactly one ace in each combination.
Answer:
No of cards in deck = 52
No. of aces = 4
Thus, no. of remaining cards = 52 - 4 .
= 48
A combination of 5 cards is formed in which exactly one ace exist and 4 are other cards
Thus, no. of selecting 1 ace out of 4 aces

Now, total group of cards = ⁴C₁ × ⁴⁸C₄
= 4 × 194580
= 778320
Thus, number of total combinations of 5 cards = 778320

Question 7.
In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl, If each cricket team of 11 must include exactly 4 bowlers?
Answer:
No. of players =11, In which 5 are bowlers
Then no. of remaining players = 17 - 5 = 12
Total 11 players have to choose,
Thus, we will select 4 players from 5 bowlers and 7 players from 12.
No. of ways to select 4 bowlers out of 5 bowlers = ⁵C₄
and no. of ways to select 7 out of 12 players = ¹²C₇
Now, total possible ways to select a team of (4 + 7 = 11) players
= ⁵C₄ × ¹²C₇

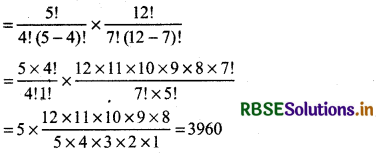
Thus. 11 players of team can be selected by 3960 ways.

Question 8.
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red bails can be selected.
Answer:
∵ No. of ways to select 2 black balls out of 5 black balls in a bag = ⁵C₂
No. of ways to select 3 red balls out of 6 red balls in a bag = ⁶C₃
Thus, no. of ways to select 2 black and 3 red balls

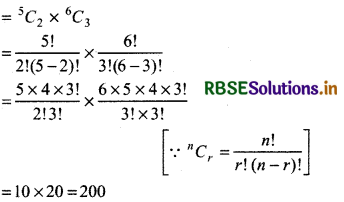
= 10 × 20 = 200
Thus, no. of ways to select 2 black and 3 red balls = 200.

Question 9.
In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specIfic courses are compulsory for every student?
Answer:
Total available programmes = 9
and student has to choose 5 courses in which 2 are compulsory.
Then, no. of ways to select 3 courses out of 7 courses

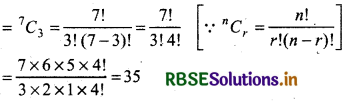
Thus, no. of ways to select 5 courses by student = 35