RBSE Solutions for Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 7 Permutations and Combinations Ex 7.3

Question 1.
How many 3-digit numbers can be formed by using the digits 1 to 9, if no digit is repeated?
Answer:
Digits from 1 to 9 are
1, 2, 3, 4, 5, 6, 7, 8, 9
Which are 9 in number. If digit is not repeated then out of these, taking 3 digit, no. of permutations = ⁹P₃
Now, ⁹P₃ = \(\frac{9 !}{(9-3) !}\)
= \(\frac{9 \times 8 \times 7 \times 6 !}{6 !}\)
= 9 × 8 × 7 = 504
Thus, required 3-digit numbers = 504

Question 2.
How many 4 digit numbers are there with no digit repeated?
Answer:
Given digits are
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Which are 10 in number
If digits are not repeated. then out of these, taking 4 digits, no. of permutations

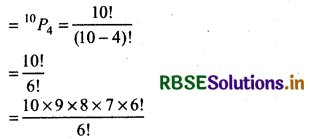
= 10 × 9 × 8 × 7 = 5040
But these permutations will include those also which starts with 0, which are actually 3-digit numbers
= ⁹P₃ = \(\frac{9 !}{(9-3) !}\) = \(\frac{9 !}{6 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 !}{6 !}\)
= 9 × 8 × 7 = 504
Thus, 4-digit numbers with no repeated digit
= 5040 - 504 = 4536

Question 3.
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7. If no digit is repeated?
Answer:
Total no. of digits = 6
Now in three digit even number, 2, 4, or 6 may be at unit place. These three digits can be arranged at unit place by 3 ways. i.e.,
No. of ways to write I digit from 2, 4, 6 = ³P₁
³P₁ = \(\frac{3 !}{(3-1) !}=\frac{3 !}{2 !}\) = 3
Now 5 digits left. Total no. of ways to choose 2 digits out of 5 digits = ⁵P₂

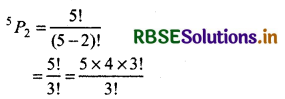
= 5 × 4 = 20
Thus, required no. of 3-digit even numbers
= ⁵P₂ × ³P₁ = 20 × 3 = 60
Thus, 3-digit even numbers = 60

Question 4.
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3. 4, 5. If no digit is repeated. How many of these will be even?
Answer:
Given digits 1, 2, 3, 4, 5, which are five in number. Then without repeated the digit numbers formed by 4 digit out of 5
= ⁵P₄
= \(\frac{5 !}{(5-4) !}\)
= \(\frac{5 !}{1 !}\) = 5 × 4 × 3 × 2 × 1 = 120 [∵ 1! = 1]
Thus, 4 digit numbers formed by given digits =120
In digits 1,2, 3,4, 5, two digits 2 and 4 are even.
By placing them at unit place even number can be formed.
Thus, total ways of writing by taking 1 digit out of 2
= ²P₁ = \(\frac{2 !}{(2-1) !}=\frac{2 !}{(1) !}\)
= 2 × 1 = 2
Now 4 digits are left. Take 3 digits from these. Thus total ways taking 3 digits out of 4 digits
= ⁴P₃ = \(\frac{4 !}{(4-3) !}=\frac{4 !}{1 !}\)
= 4 × 3 × 2 × 1 = 24
Now, by principle of mathematical calculation. 4-digit even numbers
= ⁴P₃ × ²P₁ = 24 × 2 = 28
Thus, total 4 digit even numbers = 48

Question 5.
From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman, assuming one person cannot hold more than one position?
Answer:
Total no. of members in committee = 8
No. of ways to select 1 out of 8 persons = 8

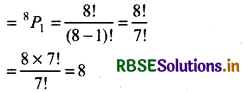
Then, no. of ways to select 1 out of remaining 7 persons
= ⁷P₁ = \(\frac{7 !}{(7-1) !}=\frac{7 !}{6 !}=\frac{7 \times 6 !}{6 !}\) = 7
Thus, total ways to select one chairman and one vice chairman
= ⁸P₁ × ⁷P₁ = 8 × 7 = 56

Question 6.
Find n, if ^{n - 1}P₃ : ⁿP₄ = 1 : 9.
Answer:
^{n - 1}P₃ : ⁿP₄ = 1 : 9

Question 7.
Find r, if
(i) ⁵P_r = 2 ⁶p_{r - 1},
(ii) ⁵P_r = ⁶P_{r - 1}.
Answer:

⇒ (6 - r) (7 - r) = 12
⇒ 42 + r² - 13r = 12
⇒ r² - 13r + 42 - 12 = 0
⇒ r² - 13r + 30 = 0
⇒ r² - 10r - 3r + 30 = 0
⇒ r(r - 10) - 3 (r - 10) = 0
⇒ (r - 10) (r - 3) = 0
⇒ r = 10, 3
But value of r cannot exceeds 5
Thus, r = 3

(ii)

⇒ (7 - r) (6 - r) = 6
⇒ 42 + r² - 13r = 6
⇒ r² - 13r + 42 - 6 = 0
⇒ r² - 13r + 36 = 0
⇒ r² - 9r - 4r + 36 = 0
⇒ (r - 9) - 4 (r - 9) = 0
⇒ (r - 9) (r - 4) = 0
⇒ r = 9 or r = 4
But r cannot exceeds 5
Thus, r =4

Question 8.
How many words, with or without meaning can be formed using all the letters of the word EQUATION, using each letter exactly once?
Answer:
There are 8 letters in word EQUATION
Thus no. of words formed by all letters

= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320
Thus, total no. of words formed by letter of word EQUATION = 40320.

Question 9.
How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if:
(i) 4 letters are used at a time.
(ii) all letters are used at a time.
(iii) all letters are used but first letter is a vowel?
Answer:
(i) There are 6 letters in the word MONDAY.
Number of words formed by 4 letters out of these, when no letter is repeated
= ⁶P₄

(ii) No. of words formed by all letters at a time.

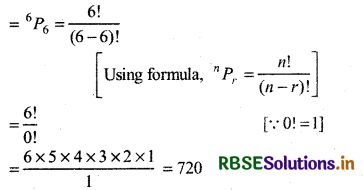
Thus, no.of words formed by 6 letters = 720

(iii) There are two vowels A and O in the word MONDAY.
No. of ways to arrange these vowels
= ²P₁ = \(\frac{2 !}{(2-1) !}=\frac{2 !}{1 !}\)
= 2 × 1 = 2
No. of words formed by remaining 5 letters
= ⁵P₅ = \(\frac{5 !}{(5-5) !}=\frac{5 !}{0 !}\) = 5! [∵ 0! = 1]
= 5 × 4 × 3 × 2 × 1
= 120
Then no of words formed by all letters, which start with vowel
= ²P₁ × 5P = 2 × 120 = 240
Thus, required no of words = 240

Question 10.
In how many of the distinct permutations of the letters in ‘MISSISSIPPI’ do the four I’s not come together?
Answer:
There are total 11 letters in the word ‘MISSISSIPPI’ In which M occurs once, I four times, S four times and P two times.
Then- no. of permutations formed by these letters 11!
= \(\frac{11 !}{4 ! 4 ! 2 !}\)
= \(\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{4 \times 3 \times 2 \times 1 \times 4 \times 3 \times 2 \times 1 \times 2 \times 1}\)
= 34650
If we take these four letters together then assume as one letter.
Then total letter will be 8 In which S four times, P two times, I and M occur once.
Thus, no. of permutations formed by all four I together 8!
= \(\frac{8 !}{4 ! 2 !}\)
= \(\frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{4 \times 3 \times 2 \times 1 \times 2 \times 1}\)
= 840
Thus, no. of permutation in which four I does not occur together
= 34650 - 840
= 33810

Question 11.
In how many ways can the letters of the word ‘PERMUTATIONS’ be arranged if the
(i) words start with P and end with S
(ii) vowels are all together
(iii) there are always 4 letters between P and S?
Answer:
There are 12 letters in word ‘PERMUTATIONS’. In which T occurs twice and remaining letters occurs once.
(i) Selected word starts with P and end with S
Then fix P and S, no of words formed by rest 10 letters

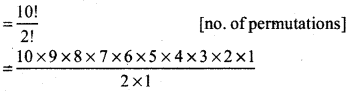
= 1814400

(ii) Total no. of vowels in word ‘PERMUTATIONS’ = 5
Vowels are all together,
so no. of ways to arrange them = ⁵P₅ = 5!
Assuming 5 vowels one letter, total no. of remaining letters
= (12 - 5 + 1) = 8
In these 8 letters, T occurs twice.
Thus, total no. of permutations formed by 8 letters = \(\frac{8 !}{2 !}\)
Thus, no. of permutations formed by all 12 letters
= 5! × \(\frac{8 !}{2 !}\)
= \(\frac{5 \times 4 \times 3 \times 2 \times 1 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1}\)
= 2419200

(iii) No. of letters in word ‘PERMUT/ VTIONS’ = 12
Here P and S are arranged such that there are always 4 letters between P and S
If we placed P at place I then we should placed S at place 6. Similarly,

Thus, P and S can be placed by 7 ways

Then total no of ways to write the permutations according to problem = 14
Now in remaining 10 letters, T occurs twice.
Thus, no. of permutations (taking 10 letters)
= \(\frac{10 !}{2 !}=\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1}\)
= 1814400
Thus, required no. of permutations
= 14 × 1814400 = 25401600
Thus, no. of permutations in which 4 letters remains between P and S.
= 25401600.