RBSE Solutions for Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 7 Permutations and Combinations Ex 7.1

Question 1. 
How many 3-digit numbers can be formed from the digits. 1, 2, 3, 4 and 5 assuming that
(i) Repetition of the digits is allowed?
(ii) Repetition of the digits is not allowed?
Answer:
(i) Three places of 3 digit number, A, B and C are shown as follows: 

First place A can be filled by any digit out of 5.
So first place can be filled by 5 ways.
Now, second place B can be filled by 5 ways, since digits can be repeated.
Similarly, third place C can be filled by 5 ways.
Thus, using 5 digits 1, 2, 3, 4 and 5, total 3 digit numbers = 5 × 5 × 5 = 125 

(ii) Three digit number using digits 1, 2, 3, 4 and 5 where digits are not repeated

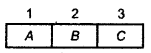
First place A can be filled by 5 ways.
Now, four digits left since digits are not repeated.
So, second place B can be filled by 4 ways.
So, third place can be filled by 3 ways.
Thus, total three digit numbers
= 5 × 4 × 3 = 60 

Alternative Method:
(i) ∵ Digit can be repeated
Total number of ways to fill unit place
= ⁵P₁ 
= \(\frac{5 !}{(5-1) !}\)
= \(\frac{5 !}{4 !}=\frac{5 \times 4 !}{4 !}\) = 5 
Similarly, tens and hundred place can be filled by 5 and 5 ways.
∴ Total numbers = 5 × 5 × 5
= 125 

(ii) When Digit are not repeated, then
Total number of ways = 5P₃

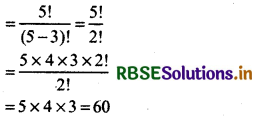
Thus, total numbers = 60

Question 2. 
How many 3 digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6. If the digits can be repeated?
Answer: 
Places of three digit number are represent by A, B and C

To till place C we can use only 2, 4 or 6.
Since number is even so place C (unit place) can be filled by 3 ways, digits may be repeat, so place B (tens place) can be filled by anyone of digit 1, 2, 3, 4, 5, 6.
Thus, B can be filled by 6 ways.
Place A (hundred place) can be filled by anyone of digits 1, 2, 3, 4, 5 or 6.
Thus, A can be filled by 6 ways.
Therefore total numbers of forming 3 digit even numbers
= 3 × 6 × 6 = 108    

Question 3. 
How many 4 letter code can be formed using the first 10 letters of the English alphabet. If no letter can be repeated?
Answer: 
According to question,
First letter of code can be select by 10 ways.
Second letter of code can be select by 9 ways. 
Similarly, third and fourth places are selected by 8 and 7 ways respectively.    -
Thus, no. of 4 letter codes
= 10 × 9 × 8 × 7
= 5040    

Question 4. 
How many 5-digit telephone numbers can be constructed using the digits 0 to 9. If each number starts with 67 and no digit appears more than once?
Answer: 
Total number of digits = 10, which are as follows 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Using these digits we have to form 5 digit telephone number and each number starts with 67.
Now out of 5, two places are filled by 6 and 7 which are definite and digits cannot be repeated so to fill third place 8 ways, are left so third place can be filled by 8 ways. Now 7 digit are left.
So fourth place can be filled by 7 ways.
Similarly, fifth place can be filled by 6 ways.
Thus, total number of five digit telephone numbers = 8 × 7 × 6 = 336

Question 5. 
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
Answer:
In tossing a coin we get two results, either ‘Head’ or ‘Tail’
Thus, every time, in tossing a coin we get Head or Tail Thus, possible outcomes in tossing 3 times
= 2 × 2 × 2 = 8    

Question 6. 
Given 5 flags of different colours. How many different signals can be generated if each signal requires the use of 2 flags, One below the other?
Answer:
Vacant places for flags are represent by A and B boxes first places A can be filled by any flag out of 5.

Thus, place A can be filled by 5 ways.
Second place B can be filled by rest 4 flags. 
Thus, place A can be filled by 4 ways.
Therefore, total number of signals = 5 × 4 = 20