RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 6 Linear Inequalities Miscellaneous Exercise

Solve the inequalities in Exercises 1 to 6.

Question 1.
2 ≤ 3x - 4 ≤ 5
Answer:
From inequality 2 ≤ 3x - 4 ≤ 5 
2 + 4 ≤ 3x ≤ 5 + 4
(Transposing - 4 to left and right side)
=>    6 ≤ 3x ≤ 9
=>    2 ≤ x ≤ 3 (Dividing by 3)
Thus x e [2,3]

Second Method : We can write the given inequality 2 ≤ 3x - 4 ≤ 5 as :
2 ≤ 3x - 4    ...(1) 
and    3x - 4 ≤ 5    ........(2)
Adding 4 to both sides of equation (1),
2 + 4 ≤ 3x - 4 + 4 
⇒ 6 ≤ 3x
⇒ 2 ≤ 3 (Dividing    by 3)
Again, adding 4 to both sides of equation (2),
3x - 4 + 4 ≤ 5 + 4 
⇒ 3x ≤ 9
⇒ x ≤ 3 (Dividing    by 3)
Now 2 ≤ x and x ≤ 3
Then x lies between 2 and 3.
Thus, the solution set is [2, 3],

Question 2.
6 ≤ - 3 (2x - 4) ≤ 12
Answer:
Inequality 6 ≤ - 3 (2x - 4) ≤ 12 can be written as:
65 - 3(2x - 4)    ...(1)
and    -3(2x - 4) ≤ 12    ...(2)
From inequality (1),
6    ≤ -6x + 12
Adding - 12 to both sides,
6 - 12 ≤ -6x + 12 - 12 
⇒ - 6 ≤ - 6x
⇒ -1 ≤ - x (Dividing both sides by 6)
⇒ 1 > x
⇒ x ≤ 1
(On multiplying by (- 1) to both sides sign < changes to >)
In inequality (2), dividing both sides by - 3,
⇒ \(\frac{-3(2 x-4)}{-3}>\frac{12}{-3}\)
⇒ 2x - 4 ≥ - 4
⇒ 2x - 4 + 4 ≥ -4 + 4
(Adding 4 to both sides)
⇒ 2x ≥ 0
⇒ x ≥ 0
Now, x lies from 0 to 1.
Thus, the solution is x ∈ (0,1]

Question 3.
-3 ≤ 4 - \(\frac{7 x}{2}\) ≤ 18
Answer:
Inequality - 3 ≤ 4 - \(\frac{7 x}{2}\) ≤ 18 can be written as:
-3 ≤ 4 - \(\frac{7 x}{2}\) .........(1)
and    4 - \(\frac{7 x}{2}\) ≤ 18 .........(2)
Adding - 4 to inequality (1), 
-3 - 4 ≤ 4 - \(\frac{7 x}{2}\) - 4
⇒ - 7 ≤ - \(\frac{7 x}{2}\)
 
Dividing both sides by - 7, we get
1 ≥ \(\frac{x}{2}\)
⇒ 2 ≥ x 
⇒ x ≤ 2
Adding - 4 to both sides of inequility (1),
-4 + 4 - \(\frac{7 x}{2}\) ≤ 18 - 4
⇒ \(\frac{7 x}{2}\) ≤ 14

Dividing both sides by - 7,
\(\frac{x}{2}\) ≥ -2
⇒ x ≥ -4
We see that x ≥ - 4 and 2 ≥ x 
⇒ 2 ≥ x ≥ -4
⇒ - 4 ≤ x ≤ 2

It means, the value of x is from - 4 to 2. Thus, the solution is x ∈ [- 4, 2]

Question 4.
-15 < \(\frac{3(x-2)}{5}\) ≤ 0
Answer:
The given inequality can be written as :
-15 < \(\frac{3(x-2)}{5}\) ............(1)
and \(\frac{3(x-2)}{5}\) ≤ 0 ........(2)
Multiplying by \(\frac{5}{3}\) to both sides of inequality (1),
-15 × \(\frac{5}{3}<\frac{3(x-2)}{5} \times \frac{5}{3}\)
⇒ -25 < x - 2
Adding 2 to both sides,
- 25 + 2 < x - 2 + 2
⇒ - 23 < x ⇒ x > - 23
And multiplying by \(\frac{5}{3}\) to both sides of inequality (2),
\(\frac{5}{3} \times \frac{3(x-2)}{5}<\frac{5}{3}\) × 0
⇒ x - 2 ≤ 0

Adding 2 to both the sides,
x - 2 + 2 ≤ 0 + 2
⇒ x ≤ 2
We see that - 23 ≤ x and x ≤ 2.
So, the value of x is from - 23 to 2.

Thus, the solution is (- 23, 2] 

Alternative Method
Given, -15 < \(\frac{3(x-2)}{5}\) ≤ 0
Multiplying by 5,
-75 < 3x - 6 ≤ 0
⇒ - 75 + 6 ≤ 3x - 6 + 6 ≤ 0 + 6
(Adding 6 to both sides)
⇒ - 69 < 3x ≤ 6
Dividing by 3,
- 23 < x ≤ 2

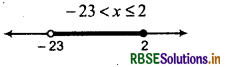
So, the value of x is greater than -23 and is equal to or less than 2.
Thus, the solution is x ∈ (- 23,2]

Question 5.
-12 < 4 - \(\frac{3 x}{-5}\) ≤ 2
Answer:
The given inequality can be written as :
-12 < 4 - \(\frac{3 x}{-5}\) ......(1)
and    4 - \(\frac{3 x}{-5}\) ≤ 2
Adding - 4 to inequality (1),
⇒ -4 - 12 < -4 + 4 - \(\frac{3 x}{-5}\)
⇒ -16 < \(\frac{3 x}{-5}\)
⇒ -16 < \(\frac{3 x}{5}\)

Multiplying both sides by 5.
⇒ - 80 < 3x
⇒ -\(\frac{80}{3}\) < x    
⇒ x > -\(\frac{80}{3}\)
Adding - 4 to both sides of inequality (2),
⇒ -4 + 4 - \(\frac{3 x}{-5}\) ≤ 2 - 4
⇒ - \(\frac{3 x}{-5}\) ≤ -2
⇒  \(\frac{3 x}{5}\) ≤ -2
⇒ \(\frac{3 x}{5}\) ≤ -2
⇒ 3x ≤ -10
⇒ x ≤ \(-\frac{10}{3}\)

We see that x > \(-\frac{80}{3}\) and x ≤ \(-\frac{10}{3}\)
So, \(-\frac{80}{3}\) and x ≤ \(-\frac{10}{3}\)

Then the value of x is from -\(\frac{80}{3}\) to \(-\frac{10}{3}\)

Thus, the solution is x ∈ \(\left(-\frac{80}{3},-\frac{10}{3}\right]\)

Alternative Method
Given, -12 < 4 - \(\frac{3 x}{5}\) ≤ 2
⇒ -12 < 4 + \(\frac{3 x}{-5}\) ≤ 2
Subtracting 4 from the inequality,
-12 - 4 < 4 + \(\frac{3 x}{5}\) - 4 ≤ 2 - 4
⇒ -16 < \(\frac{3 x}{5}\) ≤ -2

Multiplying by 5,
-16 × 5 < \(\frac{3 x}{5}\) × 5 ≤ -2 × 5
⇒ -80 < 3x ≤ -10
⇒ \(-\frac{80}{3}<\frac{3 x}{3} \leq-\frac{10}{3}\)
⇒ \(-\frac{80}{3}<x \leq-\frac{10}{3}    \)
So, the value of x is from \(-\frac{80}{3}\) to \(-\frac{10}{3}\)

Thus, the solution is x ∈ \(\left(-\frac{80}{3},-\frac{10}{3}\right]\)

Question 6.
7 ≤ \(\left(\frac{3 x+11}{2}\right)\) ≤ 11
Answer:
Given, 7 ≤ \(\left(\frac{3 x+11}{2}\right)\) ≤ 11
Multiplying both sides by 2,
⇒ 14 ≤ 3x + 11 ≤ 22
We can write it as :
14 ≤ 3x + 11    ...(1)
and    3x + 11 < 22    ......(2)
Adding - 11 to both sides of inequality (1),
14 - 11 ≤ 3x + 11 - 11
⇒ 3 < 3x
⇒ 1 < x
Again, adding -11 to both sides of inequality (2),
3x+ 11 - 11 ≤ 22 - 11 
3x ≤ 11
x ≤ \(\frac{11}{3}\)
We see that 1 ≤ x ≤ \(\frac{11}{3}\)

So, the value of x lies from 1 to \(\frac{11}{3}\)
Thus, the solution is x ∈ [1, \(\frac{11}{3}\)]

Solve the inequalities in Exercises 7 to 10 and represent the solution graphically on the number line.

Question 7.
5x + 1 > - 24, 5x - 1 < 24
Answer:
5x + 1 > - 24    ...(1)
and    5x - 1 < 24 ..........(2)
From inequality (1),
5x + 1 - 1 > -24 - 1
(Adding - 1 to both sides)
⇒ 5x > - 25
Dividing both sides by 5
x > -5
From inequation (2)
5x - 1 < 24 
Adding 1 to both the sides
5x - 1 + 1 < 24 + 1 
⇒ 5x < 25
Dividing both sides by 5,
x < 5
Now,    x > - 5 and x < 5
We see that - 5 < x < 5
i.e., the value of x is between - 5 and 5.
The solution is x ∈ (- 5, 5).
The graph of the solution is shown by the thick portion of the number line. Here, - 5 and 5 are not included.

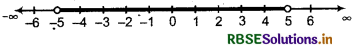
Question 8.
2(x -1) < x + 5,3(x + 2) > 2 - x 
Answer:
2(x - 1) < x + 5
3(x + 2) >2 - x 
Now, from inequality (1),
2(x - 1) < x + 5 
2x - 2 < x + 5
Adding 2 to both sides,
2x - 2 + 2 < x + 5 + 2
2x < x + 7
Subtracting x from both sides
2x - x < x - x + 7 
⇒ x    <7
Now, from inequality (2),
3(x + 2) > 2 - x 
⇒ 3x + 6 > 2 - x
Subtracting 6 from both sides
3x + 6 - 6 > 2 - x- 6
⇒ 3x > -x - 4
Adding x to both sides,
3x + x > -x + x - 4
⇒ 4x > - 4
⇒ x > -1.
⇒ x < - 1
We see that -1 < x and x < 7
So,    -1 < x < 7
i.e., the value ofx is in between -1 to 7.
The solution is x ∈ (-1, 7).
The graph of the solution is shown by the thick portion of the number line. Here, - 1 and 7 are not included.

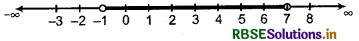
Question 9.
3x - 7 > 2(x - 6),(6 - x) > 11 - 2x
Answer:
3x - 7 > 2(x - 6)
⇒ 3x - 7 > 2x - 12
Subtracting 2x from both sides,
3x - 7 - 2x > 2x - 12 - 2x
⇒ x - 7 > -12
Adding 7 to both sides,
x - 7 + 7 > -12 + 7
⇒ x > -5 
Again, from (6 - x) > 11 - 2x
⇒ 6 - x > 11 - 2x
Adding 2x to both sides,
6 - x + 2x >11 - 2x + 2x 
⇒ 6 + x > 11
Subtracting 6 from both sides,
6 + x - 6 >11 - 6 ⇒  x > 5 
We see that x > - 5 and x > 5. 
i. e., the common value of x is x > 5.
The solution is x ∈ (5, ∞)
The graph of the solution set is shown by the thick portion of the number line.

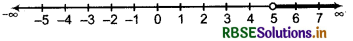
Question 10.
5(2x - 7) - 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47
Answer:
From 5(2x - 7)    - 3(2x + 3) ≤ 0
⇒ 10x -    35 - 6x - 9 ≤ 0
⇒ 4x - 44 ≤ 0
⇒ 4x ≤ 44
⇒ x ≤ 11
Now, from 2x + 19 ≤ 6x + 47
Adding -19 to both the sides,
2x + 19 - 19 ≤ 6x + 47-19 
⇒ 2x ≤ 6x + 28
Subtracting 6x from both sides,
2x - 6x < 6x + 28 - 6x
⇒ - 4x < 28
Dividing both sides by - 4, 
\(\frac{-4 x}{-4} \geq \frac{28}{-4}\)
⇒ x ≥ -7
From x ≤ 11 and x ≥ -7, we see that
-7 ≤ x ≤ 11
i. e, the values of x are from - 7 and 11.
The graph of the solution is shown by the thick postion of the number line. Here, - 7 and 11 are included.

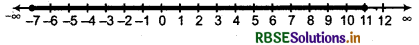
Question 11.
A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by F = \(\frac{9}{5}\)C + 32?
Answer:
Temperature is from 68°F to 77°F.
Then by F = \(\frac{9}{5}\)C + 32
⇒ \(\frac{9}{5}\)C + 32 > 68 .....(1)
and \(\frac{9}{5}\)C + 32 < 77 ..........(2)
From in inequality (1),
\(\frac{9}{5}\)C + 32 >68
⇒ \(\frac{9}{5}\)C > 68 - 32
(Adding 32 to both the sides) 9
⇒ \(\frac{9}{5}\)C > 36
(Multiplying both sides by \(\frac{9}{5}\))
C > 20

From inequality (2),
\(\frac{9}{5}\)C + 32 < 77
\(\frac{9}{5}\)C < 77 - 32
(Subtracting 32 from both sides)
⇒ \(\frac{9}{5}\)C < 45

Multiplying both side by 5,
⇒ 9C < 45 × 5
⇒ C < \(\frac{45 \times 5}{9}\)
⇒ C < 25
Thus, on the celsius scale, the range of the temperature is between 20°C and 25 °C.

Question 12.
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
Answer:
Let x litres of 2% boric acid solution be added to 640 litres of 8% boric acid solution.
Total mixture = (x + 640) litres According to given,
2% of x + 8% of 640 > 4% of (x + 640) 
and 2% of x + 8% of 640 < 6% of (x + 640)
\(\frac{2}{100}\)x + \frac{8}{100} × 640 > \(\frac{4}{100}\)(x + 640) and \(\frac{2}{100}\)x + \(\frac{8}{100}\) × 640 < \(\frac{6}{100}\)(x + 640)
⇒ 2x + 8 × 640 > 4x + 4 × 640 
and 2x + 8 × 640 < 6x + 6 × 640 
⇒ 4 × 640 > 2x and 2 × 640 < 4x 
⇒ 128 > x and 320 < x 
⇒ x < 1280 and 320 <x 
⇒ 320 < x < 1280
Thus, the number of litres of 2% boric acid solution must be more than 320 but less than 1280.

Question 13.
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Answer:
Let x litres of water be added to 1125 litres of 45% acid solution, then 25% of (x+ 1125) <45% of 1125 < 30% of (x +1125)
We have 25% of (x + 1125) < 45% of 1125
⇒ \(\frac{25}{100}\) × (x + 1125) < \(\frac{45}{100}\) × 1125
Multiplying both sides by 100, 
⇒ 25(x + 1125) <45 × 1125
Dividing both sides by 25,
x+ 1125 < 45 × 45 
x+ 1125 < 2025

Subtracting 1125 from both sides
x + 1125 < 2025 - 1125 
⇒ x < 900
Again, we have
45% of 1125 < 30% of (x +1125)
\(\frac{45}{100}\) × 1125 < \(\frac{30}{100}\) × (x + 1125)
Multiplying both sides by 100,
45 × 1125 < 30(x + 1125)
Dividing both sides by 5,
9 × 1125 < 6(x +1125)
⇒ 10125 < 6x + 6750
Subtracting 6750 from both sides
10125 - 6750 < 6x + 6750 - 6750
⇒ 3375 < 6x
Dividing both sides by 6,
5625 < x ⇒ x > 5625
We see that x < 900 and x > 562.5
i.e.,    562.5 < x <900
The value of x lies between 562.5 and 900.
Thus, the quantity of water in the mixture must be from 562.5 litres to 900 litres.

Question 14.
IQ of a person is given by the formula IQ = \(\frac{\text { MA }}{\mathrm{C A}}\) × 100, where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Answer:
Given, IQ = \(\frac{\mathrm{MA}}{12}\) × 100 and CA = 12 years
∴ IQ = \(\frac{\mathrm{MA}}{12}\) × 100 = \(\frac{25}{5}\) MA
Given, 80 ≤ IQ ≤ 140
⇒ 80 ≤ \(\frac{25}{3}\) MA ≤ 140
⇒ \(\frac{3}{25}\) × 80 ≤ MA ≤ \(\frac{3}{25}\) × 140 (Multiplying by \(\frac{3}{25}\)) 
⇒ \(\frac{48}{5}\) ≤ MA ≤ \(\frac{84}{5}\)
⇒ 9.6 ≤ MA ≤ 16.8
Thus, the mental age lies between 9.6 years and 16.8 years i.e., the mental age is alteast 9.6 years but not more than 16.8 years.