RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 6 Linear Inequalities Ex 6.3

Solve the following system of inequalities graphically:
Question 1.
x ≥ 3, y ≥ 2
Answer:
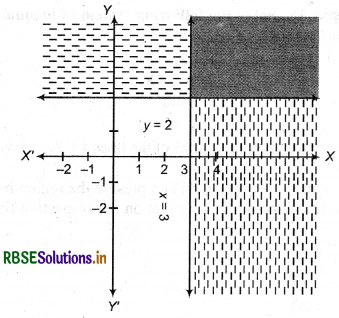
(1) Given inequality system : x ≥ 3, y ≥ 2
Corresponding equation : x = 3 ... (i)
and y = 2 .........(ii)
(2) Now, draw dotted lines x = 3 and y = 2 in cartesian plane.
(3) Clearly point (0,0) does not satisfy the inequalities x ≥ 3 and y ≥ 2. Thus solution region of inequality x ≥ 3 is right side of line x = 3 and of inequality y ≥ 2 is upper area of line y = 2. Which is shown by double shaded portion in figure.
This double shaded portion is solution region of given system of inequalities.

Question 2.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Answer:
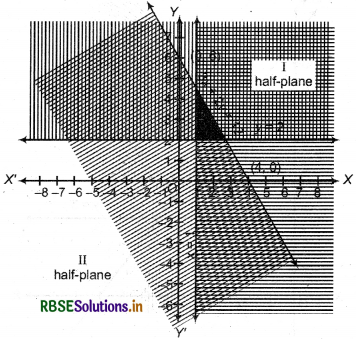
(1) Given system of inequality :
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Corresponding equation :3x + 2y = 12 ...(i)
x = 1 ..........(ii)
y = 2 .........(iii)
(2) Intersection point of line 3x + 2y = 12 with X-axis is point A = (4, 0) and with Taxis is point B = (0,6). Draw line joining these points, AB.
(3) Now draw' graph of lines x = 1 and y = 2 by dotted lines.
(4) Replacing coordinates of point (0, 0) in inequalities, we get 3 × 0 + 2 × 0 ≤ 12
or 0 < 12, which is true.
(a) Thus, point (0, 0) satisfies inequalities 3x + 2 < 12 points lies on line 3x + 2y = 12 and half plane I represents inequality 3x + 2y ≤ 12.
In graph, this region is represented by slant lines.
(b) Inequalities x ≥ 1 and y ≥ 2 does not satisfies by point (0, 0). Thus, graph of inequality x ≥ 1 is right side portion of x = 1 which is represent by horizontal lines. Graph of inequality y ≥ 2 is upper portion of y = 2 which is shown by vertical lines.
(5) Solution region of given inequalities is the common graph of all inequalities and dark shaded part in which all points on boundries are included.

Question 3.
2x + y ≥ 6,3x + 4y ≤ 12.
Answer:
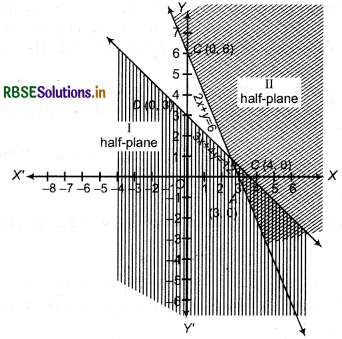
(1) Inequality : 2x + y ≥ 6,3x + 4y ≤ 12
Corresponding equations :2x + y = 6 ...(i)
3x + 4y - 12 ...(ii)
(2) Putting y = 0 in equation (i), we get
2x = 6, ⇒ x = 3
Then intersection point of line 2x + 3y = 6 and X-axis is A = (3, 0)
(3) Putting x = 0 in equation (i), we get
0 + y = 6 ⇒ y = 6
Thus, intersection point of line 2x + v = 6and Taxis is B = (0,6).
(4) Draw points A(3, 0) and B(0, 6) in cartesian plane and join dark line AB then we obtained half plane I and II.
(5) In Inequality 2x + y > 6, Putting x = 0, y = 0, we get
0 × 2 + 0 > 6 or 0 > 6, which is not true.
Thus, point (0, 0) does not satisfy inequality. Thus all points of solution of inequality lies in half plane II. This half plane is shaded by slant lines.Thus, solution region of inequality 2x + y < 6 is half plane II included all points on line 2x + y=6.
(6) Now putting y = 0 in equation (ii),
We get x = 4
Then intersection point of line 3x + 4y = 12 and X-axis will be C = (4,0)
(7) Again, putting x = 0 in equation (ii) We get y = 3
Then, intersection point of line 3x + 4y = 12 and Taxis will be D = (0,3).
(8) Draw dark line CD by joining the points C(4, 0) and D(0, 3). 

(9) Putting x = 0, y = 0 in inequality 3x + 4y ≤ 12,
We get 3 × 0 + 4 × 0 ≤ 12 or 0 ≤ 12, which is true.
Thus, point (0, 0) satisfies the inequality 3x + 4y ≤ 12 so that all the solutions of inequality lies in left part of equation 3x + 4y=12. This part is shaded by vertical lines.

Thus, solution region of inequality 3x + 4y ≤ 12 is left side area of 3x + 4y = 12 included all points on line 3x + 4y = 12. Now common area of graph of two inequalities which is double-shaded is required solution of inequalities.

Question 4.
x + y ≥ 4, 2x - y ≤ 0 
Answer:
(1) Inequality : x + y ≥ 4
Corresponding equation : x + y = 4 .. .(i)
(2) Putting y = 0 in equation (i) we get x = 4
Then point of intersection of line x + y = 4 and X-axis will be A = (4.0).
(3) Again, putting x = 0 in equation (i) we get y - 4
Then point of intersection of line x + y = 4 and X-axis will be B = (0,4)
(4) Now draw points A(4, 0) and B(0, 4) in cartesian plane and join them by dark line AB and gets half plane I and II.
(5) In inequality x + y ≥ 4, putting x = 0 and y = 0
0 + 0 ≥ 4, which is not true.
Thus, point (0, 0) does not satisfy the inequality x + y ≥ 4.
Then all points of solution of inequality will lie in half-plane II. This half-plane is shaded by slant lines.
Therefore, solution region of inequality x + y > 4 is half plane II, excluding all the points on line x+ y= 4.
(6) Inequality 2x - y > 0
Corresponding equation 2x - y = 0 ..............(ii)
(7) Clearly, line (ii) passes through origin (0, 0). Now putting y = 2 in equation (ii), we get x = 1
Then, we get a point C = (1, 2) at line 2x - y = 0.

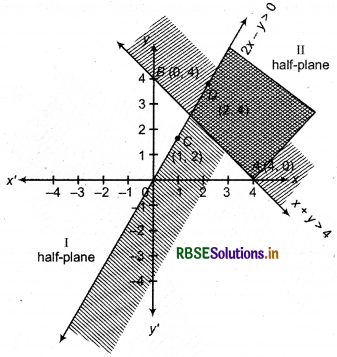
(8) Again, putting x = 2 in equation (ii) we get y = 4 So, we get point D = (2, 4) at line 2x - y=0.
(9) Draw dark line CD joining the points C(1, 2) and D(2, 4) which passes through origin (0, 0).
(10) Putting x = 1, y = 1 in inequality 2x - y > 0 
2 × 1 - 1 < 0
or 1 < 0, which is not true.
Thus point (1,1) does not satisfy inequality 2x - y > 0. So that all solutions of inequality lies in half plane II which is shaded by slant lines.
Thus, solution Region of inequality 2x - y <0 lies in half-plane II except the points on line 2x - y = 0. Common area of graph of two inequalities which is double shaded is required solution of inequalities.

Question 5.
2x - y > 1, x - 2y < - 1
Answer:
(1) Linear equation corresponding to Inequality 2x - y > 1
2x - y = 1 ...(i)
(2) Putting y = 0 in equation (i), we get x = 1/2 
So, intersection point of line 2x - y = 1 and X-axis will be A = (\(\frac{1}{2}\), 0)
(3) Again, in equation (i), putting x = 0, we get y = - 1 
So, intersection point of line 2x - y-1 and F-axis will be B = (0, -1)
(4) Mark points A(\(\frac{1}{2}\), 0) and B(0, - 1) in cartesian plane and draw dark line AB. So, we get half plane I and II 
which lies in left and right part of line 2x - y = 1 respectively.
(5) Putting x = 0, y = 0 in inequality 2x - y > 1. It is clear that point (0, 0) does not satisfy inequality since 
2 × 0 - 0 > 1
or 0 > 1, which is not true.

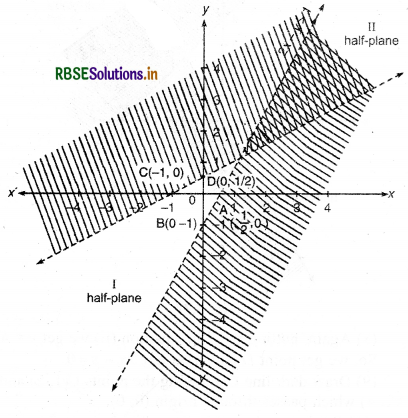
Thus, solution of inequality lies in half plane II which is shaded by slant lines.
Thus, solution region of inequality 2x - y > 1 lies in half-plane II except points lies on line 2x - y = 1.
(6) Linear equation corresponding to inequality x - 2y < -1
x - 2y = -1 ...(ii)
(7) Putting y = 0 in equation (ii) we get x = 1, then intersecting point of line x - 2y = -1 and A-axis will be C = (-1, 0).
(8) Again, putting x = 0 in equation (ii), we get y = \(\frac{1}{2}\) then intersection point of line x - 2y = -1 and Y-axis will be D = (0, \(\frac{1}{2}\))
(9) Mark the point C(-1, 0) and D(0, \(\frac{1}{2}\)) in cartesian plane and draw dark line CD.
(10) Putting x = 0, y = 0 in ineqaulity x - 2y < - 1, we get
0 - 2 × 0 < - 1
or 0 < - 1, which is not true.
Thus, point (0, 0) does not satisfy inequality x - 2y < - 1 so solution of inequality lies in that part of half plane I in which origin (0, 0) is not included. This part is shaded again,
Thus, solution region of inequality x - 2y < -1 is half plane where origin (0, 0) is not included, except all points on line x - 2y = -1.
Common area of graph if two inequalities which is double shaded, is required solution of inequalities. 

Question 6.
x + y ≤ 6, x + y ≥ 4
Answer:
(1) Linear equation corresponding to inequality
x + y ≤ 6
x + y = 6 ...(i)
(2) Putting y=0 in equation (i), we get x = 6 : Intersection point of line x + y = 6 and X-axis is obtained as A = (6, 0)

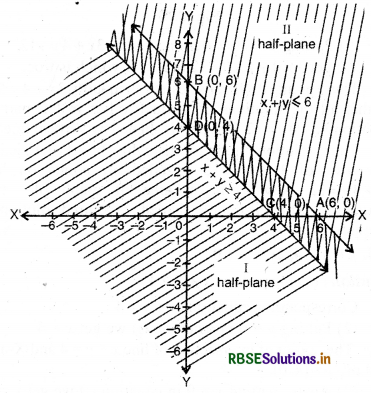
(3) Putting -v =0 in equation (i), we get y = 6.
Then point of intersection of line x + y = 6 and Y-axis is obtained as (0, 6).
(4) Mark the points A(6, 0) and B(0, 6) in cartesian plane and draw' a dark line AB so that half plane I and II are obtained,
(5) In inequality x + y ≤ 6, putting x = 0 and y = 0, 0 < 6, which is true.
Thus, point (0, 0) satisfies the inequality x + y ≤ 6. So solution of inequality lies in half plane I. This half plane is shaded by slant lines.
Thus, solution region of inequality is half plane I included all the points on line x + y = 6.
(6) Linear equation corresponding to inequality
x + y ≥ 4
x + y = 4
(7) Putting y = 0 in equation (ii). we get x 4 Then intersection point of line .v + y = 4 and Y-axis is obtained as C = (4,0)
(8) Putting x = 0 in equation (ii), we get v = 4 Then intersection point of line x + y = 4 and Y-axis
will be D = (0, 4).
(9) Mark the points C{4, 0) and D{0, 4) in cartesian plane and draw a dotted line CD.
(10) Putting x = 0 and y = 0 in inequality x + y ≥ 4 0 + 0 ≥ 4 or 0 ≥ 4, which is not true.
Thus, point (0, 0) does not satisfy the inequality x + y ≥ 4, Then all the solution of inequality lies in half plane II. This part is shaded by vertical lines.
Thus, solution region of inequality x + y ≥ 4 is half plane II included all the points on line x + y = 4.
Clearly, from the graph of two inequalities, solution of inequalities is common area i.e., double shaded portion.

Question 7.
2x + y ≥ 8,x + 2y ≥ 10
Answer:
(1) Linear equation corresponding to ineqaulity :
2x + y ≥ 8
2x + y = 8 ...........(i)
(2) Putting y = 0 in equation (i) we get x = 4,then intersection point of 2x + y = 8 and X-axis will be A = (4,0)
(3) Now, putting x = 0 in equation (i), then intersection point of line 2x + y = 8 and Y-axis will be B = (0,8),
(4) Mark the points A(4, 0) and B(0, 8) in cartesian plane and draw a dark line AB and obtained half plane 1 and IL
(5) Putting x = 0 and y = 0 in inequality 2x + y ≥ 8, we get 2 x 0 + 0 ≥ 8 or 0 ≥ 8, which is not true.
Thus, point (0, 0) does not satisfy the inequality 2x + y ≥ 8. Thus, solution of inequality lies in half palne II and shaded by slant lines.
Therefore, solution region of inequality 2x + y ≥ 8 lies in half plane II included all points on line 2x + y  8.
(6) Linear equation corresponding to inequality
x + 2y ≥ 10
x + 2y = 10 ...(ii)
(7) Putting y = 0 in equation (ii), we get x = 10. Then intersection point of line x + 2y = 10 and X-axis will be C = (10,0).
(8) Now putting x = 0 in equation (ii). we get y = 5 intersection point of line x + 2y = 10 and Y-axis will be D = (0,5).

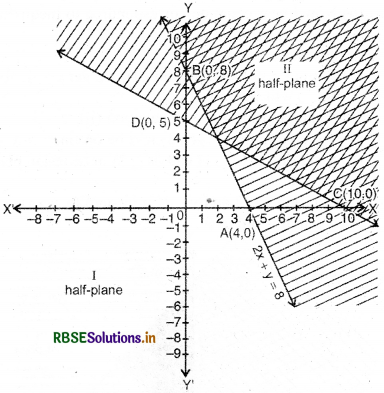
(9) Mark the points C(10, 9) and D(0, 5) in cartesian plane and draw a dark line CD.
(10) Putting x = 0 and y = 0 in inequality x + 2y ≥ 10, we get 0 + 2 × 0 ≥ 10, or 0 ≥ 10, which is not true.
Thus, point (0, 0) does not satisfy the inequality x + 2y ≥ 0
Thus, solution of inequality lies in half plane II. Shade this part.
Thus, solution region of inequality x + 2y ≥ 10 is half palne II included all points on line x + 2y = 10.
Now from graph of two inequalities. It is clear that common area of two graph i.e., double shaded area is required solution.

Question 8.
x + y ≤ 9, y ≥ x, x ≥ 0
Answer:
(1) Linear equation corresponding to inequality
x + y ≤ 9
x + y = 9  (i)
(2) Putting y = 0 in equation (i). we get x = 9, then intersection point of line x + y = 9 and X-axis will be A = (9,0). 
(3) Again, putting x = 0 in equation (i). we get y = 9, then intersection point of line x+ y = 9 and Y-axis will be B = (0, 9).
(4) Mark points A(9, 0) and B(0, 9) in cartesian plane and draw a straight line AB and obtained half plane I and II.
(5) Putting x = 0 and y = 0 in inequality x + y ≤ 9, we get 0 + 0 ≤ 9 or 0 ≤ 9, which is true. Thus point (0, 0) satisfies in equality so solution of inequality lies in half plane 1. This part is shaded by slant Sines.
Thus, solution region of inequality x + y ≤ 9 is half plan I included all points on line x + y = 9. 
(6) Now linear equation corresponding to inequality
y > x
y = x ...(ii)
(7) Putting x = 1 in equation (ii), we get y = 1, then point C = (1, 1) will lie on y = x
(8) Again, putting x = 3 in equation (ii), y = 3 Thus second point D = (3, 3) will be on line y = x.
(9) Mark points C( 1, 1) and D(3, 3) in cartesian plane and draw a dotted line.
(10) Putting x = 2 and y = 1 in ineqaulity y > x 
1 > 2, which is not true

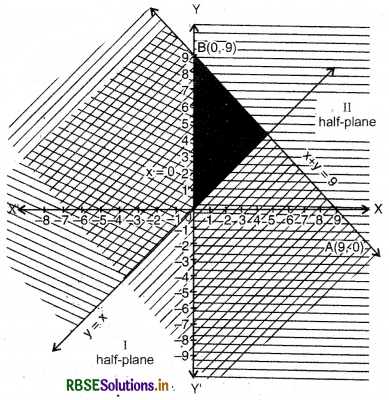
Thus, point (2, 1) does not satisfy inequality y > x. Thus, solution of inequality lies that side of line y = x where point (2, 1) does not exist. This part is shaded by slant lines.
Thus, solution region of inequality y > x is that part of y = x where (2,1) does not exist, except all points on y = x.
(11) Linear equation corresponding to inequality x ≥ 0
x = 0
Clearly, x = 0 shows Y-axis.
Thus, expansion of graph x ≥ 0 is right side of Y-axis included points of Y-axis (x = 0) as shown in graph by horizontal lines.
Thus, dark shaded portion, included x + y-9 and all points of x = 0 represents solutions of inequalities. 

Question 9.
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Answer:
(1) Given inequality : 5x + 4y ≤ 20
Corresponding equation 5x + 4y = 20 ...(i)
(2) In equation (i), putting y = 0 we get x = 4, then intersection point of line 5x + 4y = 20 and X-axis will be A =(4,0).
(3) Putting x = 0 in equation (i) we get y = 5, then intersection point of line 5x + 4y = 20 and F-axis will be B = (0, 5).
(4) Mark points A(4, 0) and B(0, 5) in cartesian plane and draw a straight line AB so half plane I and II are obtained.
(5) Putting x = 0 and y = 0 in inequality 5x + 4y ≤ 20
5 × 0 + 4 × 0 ≤ 20
or 0 ≤ 20, which is true.
Thus, point (0, 0) satisfies inequality 5x + 4y ≤ 20. Then, solution of inequality will lie that side of line 5.x + 4y = 0 where point (0, 0) exists. This part is shaded by horizontal lines.

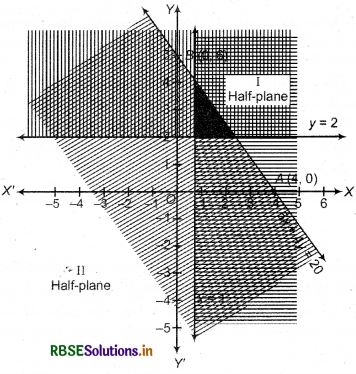
Thus, solution region of inequality 5x + 4y ≤ 20 is half plane I under the line AB included all points on line 5x + 4y = 20.
(6) Linear equation corresponding to inequality x ≥ 1
x = 1 ...(ii)
and linear equation corresponding to inequality y  ≥ 2 
y = 2 .........(iii)
(7) Now draw graph of x = 1 and y = 2,
(8) Solution of inequality x ≥ 1 will lie at right side of line x = 1. Similarly, solution of y ≥ 2 will lie above the line y = 2. These two parts are shaded by vertical and slant lines respectively.
Common area of inequalities i.e. dark shaded area is required solution.

Question 10.
3x + 4y ≤ 60,
x + 3y ≤ 30, x ≥ 0, y ≥ 0
Answer:
(1) Linear equation corresponding to given inequality 3x + 4y ≤ 60 .
3x + 4y = 60 ............(i) 
(2) Putting y = 0 in equation (i), x = 20, then intersection point of line 3x + 4y = 60 and X-axis will be A = (20, 0).
(3) Again, putting x = 0 in equation (i), y = 15 then intersection point of line 3x + 4y = 60 and 7-axis will be B = (0,15).
(4) Mark the points 4(20, 0) and 5(0, 15) in cartesian plane and draw a straight line AB so that half plane I and II are obtained.
(5) Putting x = 0 and y = 0 in inequality 3x + 4y ≤ 60
3 × 0 + 4 × 0 ≤ 60 
or 0 ≤ 60, which is true.

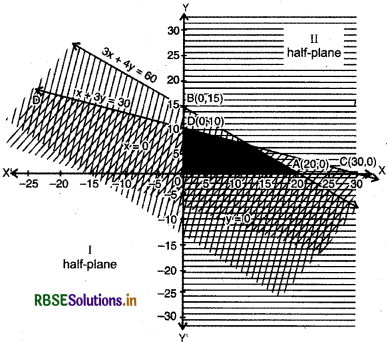
Thus, point (0,0) satisfies inequality 3x + 4y < 60.Then solution of inequality lies at left-side of line 3x + 4y = 60. In which (0, 0) exists i.e. will lie in half plane I. This part is shaded by horizontal line. Thus, solution region of inequality 3x + 4y ≤ 60 is that part of 3x + 4y = 60. In which point (0, 0) exists, included all the points on line 3x + 4y = 60 i.e., half plane I.
(6) Linear equation corresponding to inequality
x + 3y ≤ 30
x + 3y = 30 ...........(ii)
(7) Putting y = 0 in equation (ii), we get x = 30, then intersection point of line x + 3y = 30 and X-axis will be C = (30,0). .
(8) Again, in equation (ii), putting x = 0 we get y = 10 then intersection point of line x + 3y = 3 and Y-axis will be D = (0,10).
(9) Mark points C(30, 0) and D(0, 10) in cartesian plane and draw a straight line CD.
(10) Putting x = 0 and y = 0 in inequality x + 3y ≤ 30
0 + 3 × 0 ≤ 30 or 0 ≤ 30, which is true.
Thus, point (0, 0) satisfies inequality x + 3y ≤ 30. Thus, solution of inequality lies under the line x + 3y = 30. This part is shaded by vertical lines.
Thus solution region of inequality x + 3y ≤ 30 is lower part of line x + 3y = 30 included all the points on this line. Similarly draw the graph of x ≥ 0 and y ≥ 0.
Then common area of all the inequalities i.e., dark shaded region is required solution of given inequalities.

Question 11.
2x + y ≥ 4, x + y ≤ 3, 2x - 3y ≤ 6
Answer:
(1) Linear equation corresponding to inequality 2x + y ≥ 4
2x + y= 4 ,..(i)
(2) Putting y = 0 in equation (i), we get x = 2, then intersection points of equation 2x + y = 4 and X-axis will be A = (2, 0).
(3) Putting x = 0 in equation (i), y = 4, then . intersection point of equation 2x + y = 4 and Y-axis will be B = (0, 4).
(4) Plot the points A(2, 0) and B(0, 4) in cartesian plane and draw a straight line AB.
(5) Putting x = 0 and y = 0 in inequality 2x + y ≥ 4
2 × 0 + 0 ≥ 4
or 0 ≥ 4, which is not true.
Thus, point (0, 0) does not satisfy the inequality 2x + y ≥ 4. So, solution of inequality lies that side of equation 2x + y = 4, where point (0, 0) does not exist. This part is shaded by vertical lines.
Thus, solution region of inequality 2x + y ≥ 4 is upper- part of line included all points on line 2x + y = 4.
(6) Linear equation corresponding to inequality x + y ≤ 3

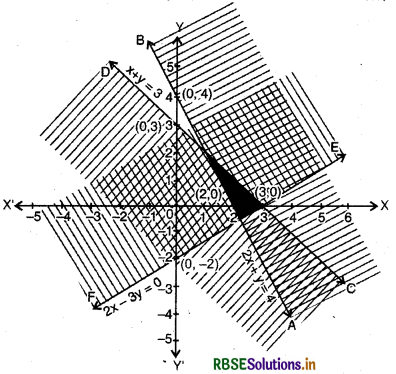
(7) Putting y = 0 in equation (ii), x = 3, then intersection point of line x + y = 3 and X-axis- will be C = (3, 0).
(8) Putting x=0 in equation (ii) we get y = 3, then intersection point of line x + y = 3 and Y-axis will be D = (0,3).
(9) Plot the points C(3, 0) and D(0, 3) in cartesian plane and draw a straight line CD.
(10) Putting x = 0 and y = 0 in inequality x + y ≤ 3
0 + 0 ≤ 2, which is true.
Thus, point (0, 0) satisfies inequality x + y = 3.
Then, solution of inequality lies in that half plane where point (0, 0) lies. This part is shaded by horizontal lines. Then, solution region of inequality x + y ≤ 3 is that part of x + y = 3 where point (0, 0) lies, included the points on line x + y = 3.
(11) Linear equation corresponding to inequality 2x - 3y ≤ 6
2x - 3y = 6 ...........(iii)
(12) Putting y = 0 in equation (iii), we get x - 3, then intersection point of line 2x - 3y = 6 and X-axis will be E = (3, 0).
(13) Putting x = 0 in equation (iii), we get y = - 2, then intersection point of line 2x - 3y = 6 and Y-axis will be F = (0, -2).
(14) Now, plot the points E(3, 0) and F(0, - 2) in cartesian plane and draw a straight line EF.
(15) Putting x = 0, y = 0 in inequality 2x - 3y < 6
2 × 0 - 3 × 0 ≤ 6 ,
or 0 ≤ 6, which is true.
Thus, point (0, 0) satisfy inequality 2x - 3y ≤ 6, then solution of inequality will be half plane where point (0, 0) exist, included all points on line 2x - 3 y = 6. This part is shaded by slant lines.
Now, resulting solution of all inequalities is common region of their graph i.e., dark shaded part is required solution of inequalities.

Question 12.
x - 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1.
Answer:
(1) Linear equation corresponding to inequality
x - 2y ≤ 3
x - 2y = 3 ...(i)
(2) Putting y = 0 in equation (i), we get x = 3, then intersection point of line x - 2y = 3 and X-axis will be A = (3,0).
(3) Putting x = 0 in equation (i), y = -\(\frac{3}{2}\) then Intersection point of line x - 2y = 3 and Y-axis will be B = (0, -\(\frac{3}{2}\))
(4) Plot the points A(3, 0) and B(0, -\(\frac{3}{2}\)) in cartesian plane and draw straight line AB.

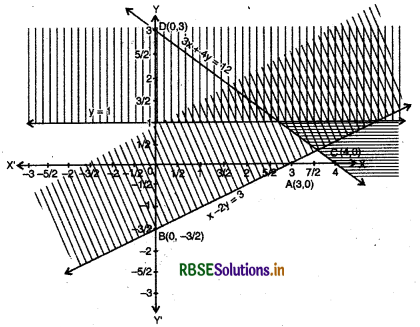
(5) Putting x = 0, and y = 0 in inequality x - 2y ≤ 3, we get 0 - 2 × 0 ≤ 3 or 0 < 3, which is true.
Thus, point (0,0) satisfies inequality. Then solution of inequality lies that side of equation x - 2y = 3, where (0,0) exists. This half plane is shaded by horizontal lines.
(6) Linear equation corresponding to inequality 3x + 4y ≥ 12
3x + 4y = 12 ...........(ii)
(7) Putting y = 0 in equation (ii), we get x = 4, then intersection point of line 3x + 4y = 12 and X-axis will be C = ( 4,0).
(8) Putting x = 0 in equation (ii), we get y = 3, then intersection point of line 3x + 4y = 12 and 7-axis will be D = (0,3).
(9) Plot the points C(4, 0) and D(0, 3) in cartesian plane and draw a straight line CD.
(10) Putting x = 0, y = 0 in inequality 3x + 4y ≥ 12
3 × 0 + 4 × 0 ≥ 12
or 0 ≥ 12, which is not true.
Thus, point (0, 0) does not satisfy the inequality 3x + 4y ≥ 12. Then, solution of inequality will lie in that half palne where point (0, 0) does not exist. This part is shaded by vertical lines.
(11) Now, draw graph of inequalities x ≥ 0 and y ≥ 1. Graph of x = 0 is Y-axis and for y ≥ 1 is y = 1. Right side of Y-axis and upper part of line y = 1 is shaded.
Common region of all inequalities is shaded , which is required solution of inequalities.

Question 13.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0.
Answer:
(1) Linear equation corresponding to inequality: 
4x + 3y ≤ 60 
4x +3y = 60
(2) Putting y = 0 in equation (i), we get x = 15, then intersection point of line 4x + 3y =60 and X-axis will be A = (15, 0).
(3) Putting x = 0 in equation (i), we get y = 20, then intersection point of line 4x + 3y = 60 and Y-axis will be B = (0, 20)

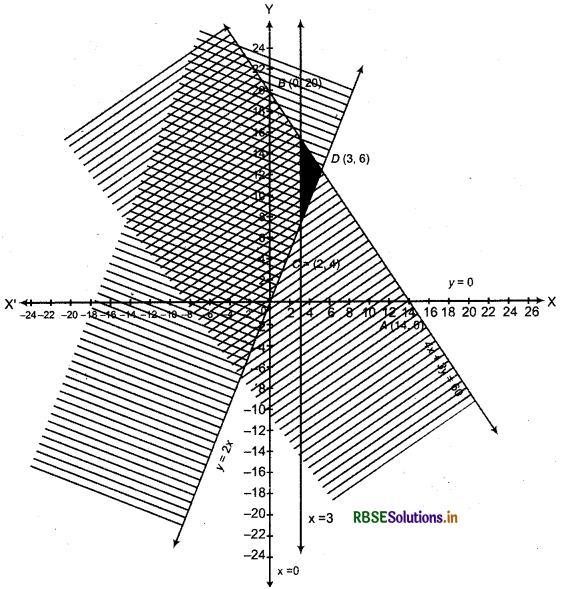
(4) Plot the points A(15, 0) and B(0, 20) in cartesian plane and draw line AB.
(5) Putting x = 0 and y = 0 in inequality 4x + 3y ≤ 60
4 × 0 + 3 × 0 ≤ 60
or 0 ≤ 60, which is true.
Thus, point (0, 0) satisfies inequality 4x + 3y ≤ 60. Then, solution of inequality will be that side of line
4x + 3y = 60 where origin(0, 0) lies. This part is shaded by horizontal lines.
(6) Linear equation corresponding to inequality y ≥ 2x 
y = 2x ...(ii)
(7) Putting x = 2 in equation (ii), y = 4, then we get a point C = (2,4).
(8) Putting x = 3 in equation (ii), y = 6, then we get second point D = (3,6).
(9) Plot the points C(2, 4) and D(3, 6) draw a straight line CD which is graph of y = 2x.
(10) In inequality y ≥ 2x, putting x = 20 and y = 10
10 ≥ 2 × 20
or 10 ≥ 40, which is not true.
Thus, it is clear that point (20, 10) does not satisfy the inequality so all the solutions of inequality will lie in that part of line y = 2x where point (20, 10) does not exist. This part is shaded by vertical lines.
Thus, solution region of inequality y ≥ 2x is half plane where point (20, 10) does not exist, included all the points on line y = 2x.
(11) Linear equations corresponding to inequalities x ≥ 3, x ≥ 0 and y ≥ 0 are
x = 3, x = 0 and y = 0.
Draw their graphs. Here graph of x ≥ 3 and x ≥ 0 will expand in right side of lines x = 3 and x = 0 and graph of y ≥ 0, y=0 will be upper part of X-axis.
Thus, common region of graph of inequalities which is dark is required solution of inequalities. 

Question 14.
3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0.
Answer:
(1) Linear equation corresponding to inequality : 3x + 2y ≤ 150
3x + 2y = 150 ............(i)

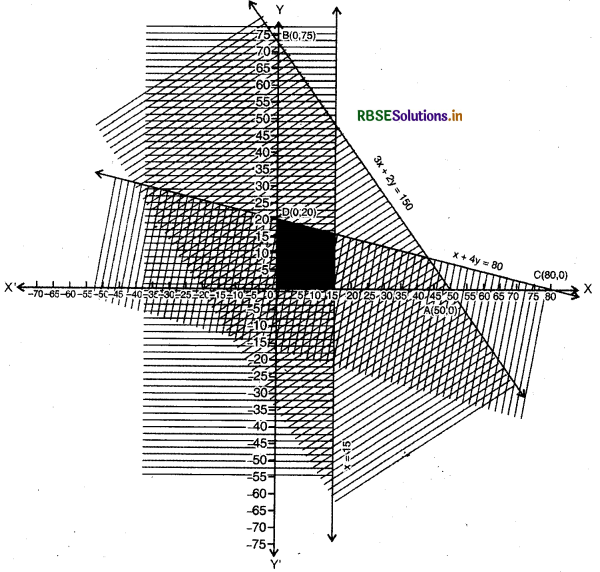
(2) Putting y = 0 in equation (i) we get x = 50, then intersection point of line 3x + 2 v = 150 and X-axis will be A = (50, 0).
(3) Putting x = 0 in equation (i), we get y = 75, then intersection point of line 3x + 2y = 150 and T-axis will be B = (0, 75).
(4) Plot the points A(50, 0) and B(0, 75) in cartesian plane and draw straight line AB.
(5) Putting x = 0 and y = 0 in inequality 3x + 2 y ≤ 150
3 × 0 + 2 × 0 ≤ 150
or 0 ≤ 150, which is true.
Thus, point (0, 0) satisfies inequality. Then solution of inequality will lie in that half plane of line 3x+2y = 150 where point (0, 0) exists. This half plane is shaded by horizontal lines.
(6) Linear equation corresponding to inequality
x + 4 y ≤ 80
x + 4y = 80 .........(ii)
(7) Putting y = 0 in equation (ii), we get x = 80, then intersection point of line x + 4y = 80 and X-axis will be C = (80,0).
(8) Putting x = 0 in equation (ii), we get y = 20, then intersection point of line x + 4y-80 and Y-axis will be D = (0,20).
(9) Plot the points C(80, 0) and D(0, 20) in cartesian plane and draw straight line CD.
(10) Putting x = 0 and y = 0 in inequality x + 4y ≤ 80, we get 0 + 4 × 0 ≤ 80 or 0 ≤ 80, which is true.
Thus, point (0, 0) satisfies inequality x + 4y ≤ 80. Then solution of inequality will lie in that half plane of line x + 4y = 80 where point (0, 0) exists. This part is shaded by vertical lines.
(11) Draw line x = 15 corresponding to inequality x ≤ 15 graph of inequality x ≤ 15 expands in the left of line x = 15.
(12) Line corresponding to inequality y ≥ 0 is y = 0 i.e. X-axis. Expansion of graph y>0 is upper part of X-axis, Now common region of graph of all four inequalities dark shaded will be required solution of inequalities.

Question 15.
x + 2y ≤ 10, x + y ≥ 1, x - y ≤ 0, x ≥ 0, y ≥ 0.
Answer:
(1) Linear equation corresponding to inequality: x + 2y ≤ 0 
x + 2y = 10 ..........(i)
(2) Putting y = 0 in equation (i), we get x = 10, then intersection point of line x + 2y = 10 and X-axis will be A = (10,0).
(3) Putting x = 0 in equation (i) we get y = 5, then intersection point of line x + 2y = 10 and Y-axis will be £=(0,5).
(4) Plot the points A(10, 0) and B(0, 5) in cartesian plane and draw a straight line AB.
(5) Putting x = 0 and y = 0 in inequality x + 2y ≤ 10
0 + 2 × 0 ≤ 10 or 0 ≤ 10, which is true.
(6) Linear equation corresponding to inequality x + y ≥ 1
x + y = 1 ...(ii)
(7) Putting y = 0 in equation (ii), we get x = 1, then intersection point of line x + y = 1 and X-axis will be C = (1, 0).
(8) Putting x = 0 in equation (ii), we get x = 1, then intersection point of line x + y = 1 and Y-axis will be D = (0, 1)
(9) Plot the points c(1, 0) and D(0, 1) in cartesian plane and draw a straight line CD.
(10) Putting x = 0 and y = 0 in inequality x + y ≥ 1,
0 + 0 ≥ 1
or 0 ≥ 1, which is not true.
Thus, point (0, 0) does not satisfy inequality x + y ≥ 1. Then solution of inequality will be upper part of line x + y = l where point (0, 0) does not exist. This part is shaded by vertical lines.
(11) Linear equation corresponding to inequality
x - y ≤ 0
x - y = 0 ...(iii)
(12) Putting x = 2 in equation (iii) we get point E = (2, 2).
(13) Putting y = 4 in equation (iii) we get another point F = ( 4,4).
(14) Draw a straight line EF joining the points E(2, 2) and F(4, 4).
(15) Putting x = 3 and y = 2 in inequality x - y ≤ 0, 
3 - 2 ≤ 0
or 1 ≤ 0, which is not true.

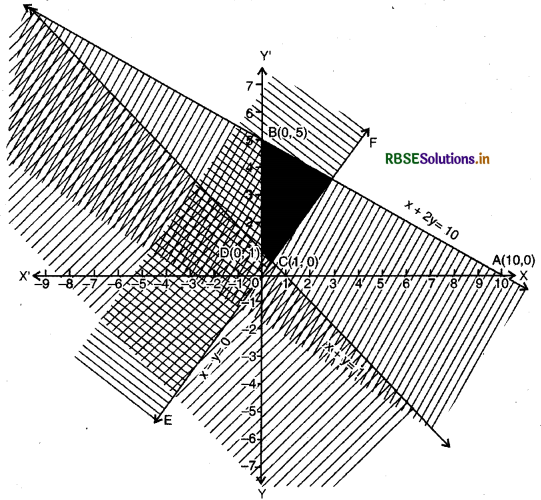
Thus, point (3, 2) does not satisfy the inequality x - y ≤ 0. Then solution of inequality x - y ≤ 0 will be in that half plane of line x - y = 0 where point (3, 2) will not be exist. This part is shaded by slant lines.
(16) Graph of inequalities x ≥ 0 and y ≥ 0 will be right side of lines x = 0 and y = 0 i.e. Y-axis and X-axis.
Common region of all the inequalities is shown by dark shaded which is required solution region of given inequalities.