RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 6 Linear Inequalities Ex 6.2

Solve the following inequalities graphically in two dimensional plane.

Question 1.
x + y < 5.
Answer:
(i) Given Inequality : x + y < 5 
and equation corresponding to it.
x + y = 5 ...(i)
(2) Putting y = 0 in equation (i), we get x = 5 
Thus point of intersection of x-axis and line x + y = 5

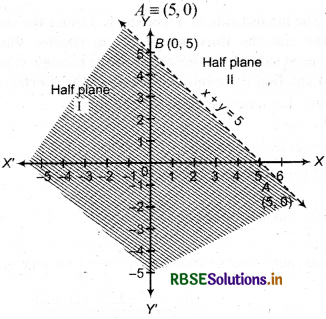
(3) Putting x = 0 in equation (i), we get y = 5 
Thus, intersection point of 7-axis and line x + y = 5
B = (0, 5)
(4) Draw a dotted line joining the point 4(5, 0) and 6(0, 5) in AB cartesian plane as shown in figure.
(5) Now, replacing coordinates of (0, 0) in inequality x + y < 5, 0 + 0 < 5, which is true.
Thus, point (0, 0) satisfies inequality.
Then, solution-region of inequality is 1 which has shaded.

Question 2.
2x + y > 6
Answer:
(1) Linear equation corresponding to given inequality :
2x + y > 6
2x + y = 6 ...(i)
(2) Putting y = 0 in equation (i), x = 3
Then A = (3,0) will be intersection point of line (i) and X-axis.
(3) Now in equation (i), putting x = 0, y = 6.

Thus, point B s (0,6) will be intersection point of line 2x + y—6 and 7-axis.
(4) Now marked the points 4(3,0) and 6(0,6) in cartesian plane and by joining them draw- a dark black line AB as shown in the figure.
(5) Now, putting x = 0 and y = 0 in inequality 2x + y ≥ 6 then 2 × 0 + 6 ≥ 6
or 0 ≥ 6, which is not true.
Thus, point (0, 0) does not satisfy the given inequality therefore solution region of inequality is not half plane I.
Then solution region of inequality will be half plane II including all the points on 2x + y = 6. This solution region is represented by shaded part.

Question 3.
3x + 4y ≤ 12
Answer:
(1) Given inequality : 3x + 4y ≤ 12
Corresponding linear equation 3x + 4y = 12 ...(i)
(2) Now, putting y = 0 in equation (i), x = 4

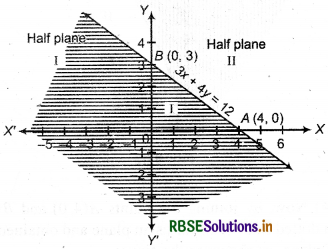
Then A = (4, 0) will be intersection point of line 3x + 4y = 12 and x-axis.
(3) Again in equation (i) putting x = 0, y = 3
Then point B = (0, 3) will be intersection point of line 3x + 4y = 12 and y-axis.
(4) Mark the points 4(4,0) and 6(0, 3) in cartesian plane and draw a dotted line 46 by joining them so that we get I and II half planes as shown in the figure.
(5) Now putting x = 0, y=0 in inequality 3x + 4y ≤ 12 Then 3 × 0 + 4 × 0 ≤ 12
or 0 ≤ 12, which is true,
i.e., (0, 0) satisfies inequality
Thus., solution region of inequality will be half plane I including points on the line 3x + 4y = 12 which is shown by shaded part.

Question 4.
y + 8 ≥ 2x
Answer:
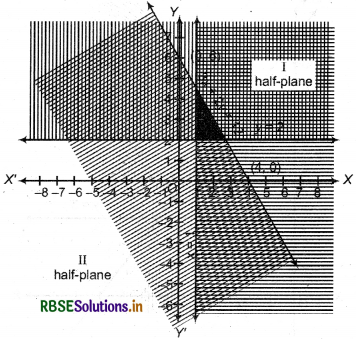
(1) Given inequality : y + 8 ≥ 2x
Corresponding equation y + 8 = 2x ... (i)
(2) Putting y = 0 in equation (i), x = 4
Then A = (4, 0) will be intersection point of line y + 8 = 2x and X-axis.
(3) Again, putting x = 0 in equation (i), y = - 8 
Thus, point 5 =(0, -8) will be intersection point of line y + 8 = 2x and Y-axis.

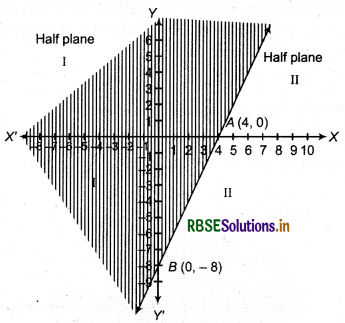
(4) Now, by joining the points A(4, 0) and 5(0, -8) draw a dotted line AB in cartesian plane and obtained I and II half plane, as shown in the figure.
(5) Now, putting x = 0 and y = 0 m inequality
y + 8 ≥ 2x 
0 + 8 ≥ 2 × 0
or 8 ≥ 0, which is true.
Thus, point (0, 0) satisfies inequality.
Then solution of inequality lies in half plane I as shown by shaded part.
Thus, half plane I, including all points of line AB is solution region of given inequality.

Question 5.
x - y ≤ 2
Answer:
(1) Given inequality : x - y ≤ 2
Corresponding linear equation x - y = 2 ...(i)
(2) Putting y = 0 in equation (i), we get
x = 2
Then point A = (2,0) will be intersection point of line x - y = - 2 and X-axis.
(3) Again, in equation (i) putting x = 0, we get
y = -2
Thus, point B = (0, -2) will be intersection point of line x - y = -2 and y-axis.
(4) Mark the points A(2, 0) and 5(0, - 2) in cartesian plane draw a dotted line AB so half plane I and II are obtained as shown in the figure.

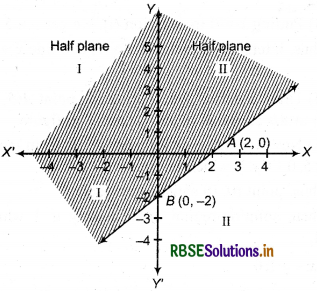
(5) Now putting x = 0, y = 0 in inequality x - y ≤ 2 then 0 - 0 ≤ 2 or 0 ≤ 2, which is true.
Thus, point (0, 0) satisfies the inequality.
Then solution region of inequality will be half plane I which is shaded.
Thus, half plane I, included all points on line x - y = 2, is solution region of given inequality x - y ≤ 2.

Question 6.
2x - 3y > 6
Answer:
(1) Given inequality : 2x - 3y > 6
Corresponding equation 2x - 3 y = 6 ... (i)
(2) Putting y = 0 in equation (i) x = 3 is obtained ;
Thus point A = (3,0) will be intersection point of line 2x - 3 y = 6 and X-axis.
(3) Again, in equation (i), putting x = 0, y = -2 is obtained.
Thus, point 5 s(0, -2) will be intersection point of line 2x - 3 y = 6 and Y-axis.
(4) Now, mark points A(3, 0) and B(0, - 2) in cartersian plane and draw dotted line AB so that half plane I and II are obtained as shown in the figure.

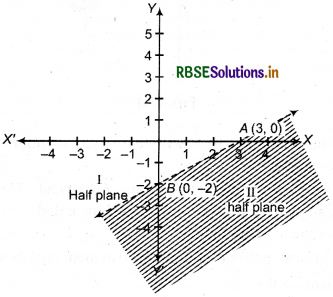
(5) Now in inequality 2x - 3y > 6
Putting x = 0 and y = 0, then 2 × 0 - 3 × 0 > 6 or 0 > 6, which is not true.
Thus, point (0, 0) does not satisfy the inequality. Thus, half plane II will be solution of inequality which is shaded part of the figure.

Question 7.
-3x + 2y > -6
Answer:
(1) Given inequality is -3x +2 y > -6
Corresponding equation -3x + 2y = -6 ...(i)
(2) In equation (i), putting y = 0, we get x = 2 
Thus point A = (2,0) will be intersection point of line -3x + 2y = 6 and X-axis.
(3) Again, putting x = 0 in equation (i) we get y = - 3 Thus point 5 = (0, -3) will be intersection point of line -3x +2y = 6 and T-axis.
(4) Now mark points A(2, 0) and 5(1, -3) in cartesian plane and draw a dark line AB.
Thus, half plane I and half plane II are obtained as shown in figure.
(5) Now putting x = 0 and y = 0 in inequality -3x +2y ≥ -6
then -3 × 0 + 2 × 0 ≥ -6 or 0 ≥ -6, which is true.
Thus, point (0, 0) satisfies given inequality

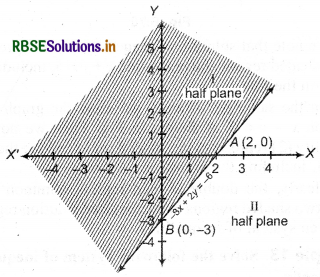
Thus, solution region of inequality will be half plane I included all the points on line AB.

Question 8.
3y - 5x < 30
Answer:
(1) Given inequality : 3y - 5x < 30
Corresponding equation 3y - 5x -30 .......(i)
(2) Putting y = 0 in equation (i), we get x = - 6 Thus, point A = (-6, 0) will be intersection point of line 3y - 5x = 30 and X-axis.
(3) Again, putting x = 0 in equation (i) we get y = 10 
Thus, point B = (0, 10) will be intersection point of
line 3y - 5x = 30 and point B = (0, 10).
(4) Now mark the points A (-6, 0) and 5(0, 10) in cartesian plane draw a dotted line AB so that half plane I and half plane II are obtained as shown in the figure.
(5) Now, in inequality 3y - 5x < 30 Putting x = 0 and y = 0, we get
3 × 0 - 5 × 0 < 30
or 0 < 30, which is true.

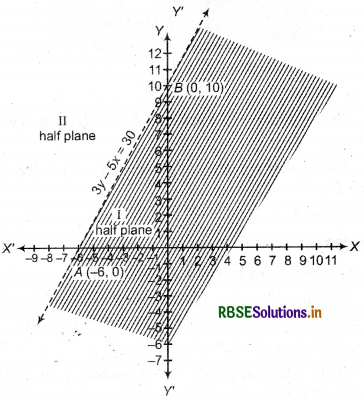
Thus, point (0, 0) satisfies given inequality.
Then solution region of given inequality will be half plane I as shaded in the figure.
Therefore, half plane 1 will be solution region of given inequality 3 y - 5x < 30.

Question 9.
y < -2
Answer:
(1) Given inequality : y < -2
Its corresponding equation y = -2 ..........(i)
(2) Line y = - 2 is parallel to A'-axis and lie at a distance of - 2 unit. Draw this line and noted by AB. Thus two half plane I and II are obtained as shown in the figure.
(3) Putting x = 0 and y = 0 in given inequality. 0 < -2, which is not true.
Thus, point (0, 0) does not satisfy the given inequality y < -2.

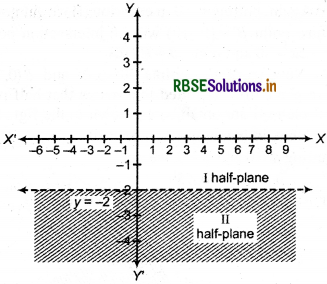
Thus, solution of inequality will be half plane II which is shaded.
Thus, solution region of given inequality will be half plane II.

Question 10.
x > -3
Answer:
(1) Given inequality : x > -3
Corresponding equation x = -3 ...(i)
(2) Line x = -3 is parallel to 7-axis and lies at a distance of-3 unit. It is denoted by dotted line AB.
(3) We get two half planes I and II
(4) In given inequality x > - 3, putting x =0, y = 0 we get 0 > -3, which is true.
Thus point (0, 0) satisfies given inequality.
Then half plane I is solution of inequality, which is shaded..

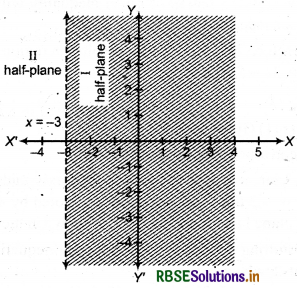
Thus, solution region of given inequality will be half-plane I.