RBSE Solutions for Class 11 Maths Chapter 6 रैखिक असमिकाएँ Ex 6.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 6 रैखिक असमिकाएँ Ex 6.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 6 रैखिक असमिकाएँ Ex 6.1

प्रश्न 1.
हल कीजिए : 24x < 100, जब
(i) x एक प्राकृत संख्या है।
(ii) x एक पूर्णांक है।
हल:
दिया गया है कि 24x < 100
या \(\frac{24 x}{24}<\frac{100}{24}\) [ नियम (iii) के अनुसार ]
या x < \(\frac{100}{24}=\frac{25}{6}\)

(i) यदि x एक प्राकृत संख्या है तो हल = {1, 2, 3, 4}

(ii) यदि  x  एक पूर्णांक है तो हल = {...... -3, -2, -1, 0, 1, 2, 3, 4}

प्रश्न 2.
हल कीजिए : -12x > 30, जब
(i) x एक प्राकृत संख्या है।
(ii) x एक पूर्णांक है ।
हल:
दिया गया है कि - 12x > 30
या \(\frac{-12 x}{-12}<\frac{30}{-12}\) [ नियम (iv) के अनुसार ]
या x < \(\frac{-30}{12}\)
या x < \(\frac{-5}{2}\)

(i) यदि x एक प्राकृत संख्या है तो इसका कोई हल नहीं है।

(ii) यदि x पूर्णांक संख्या है तो हल (... - 5, 4, - 3} है।

प्रश्न 3.
हल कीजिए : 5x - 3 < 7, जब
(i) x एक पूर्णांक है ।
(ii) x एक वास्तविक संख्या है।
हल:
दिया गया है कि 5x - 3 < 7
या 5x - 3 + 3 < 7 + 3 [नियम (i) के अनुसार ]
या 5x < 10
⇒ \(\frac{5 x}{5}<\frac{10}{5}\)
या x < 2
(i) यदि x एक पूर्णांक संख्या है तो हल {.... - 2, – 1, 0, 1}
(ii) यदि x एक वास्तविक संख्या है तो हल x ∈ ( - 00, 2)

 

प्रश्न 4.
हल कीजिए : 3x + 8 > 2, जब
(i) x एक पूर्णांक है।
(ii) x एक वास्तविक संख्या है।
हल:
दिया गया है कि 3x + 8 > 2
या 3x + 8 - 8 > 2 - 8 [नियम (ii) के अनुसार ]
या 3x > - 6
⇒ \(\frac{3 x}{3}>\frac{-6}{3}\)
⇒ x > - 2
(i) यदि x एक पूर्णांक संख्या है तो हल {-1, 0, 1, 2, 3, ......}
(ii) यदि x एक वास्तविक संख्या है तो हल x ∈ (−2, ∞)

निम्नलिखित प्रश्न 5 से 16 तक वास्तविक संख्या x के लिए हल कीजिए-

प्रश्न 5.
4x + 3 < 5x + 7
हल:
प्रश्नानुसार 4x + 3 < 5x + 7
या 4x + 3 - 3 < 5x + 7 - 3 [नियम (ii) के अनुसार]
या 4x < 5x + 4
या 4x - 5x < 6x - 6x + 4 [नियम (ii) के अनुसार]
या - x < 4
या x > - 4
⇒ x ∈ (– 4, 0)
∴ दी गई असमिका का हल क्षेत्र = (- 4, 0)

प्रश्न 6.
3x - 7 > 5x – 1
हल:
प्रश्नानुसार 3x - 7 > 5x - 1
या 3x - 7 + 7 > 5x - 1 + 7 [नियम (i) के अनुसार]
या 3x > 5x + 6
या 3x - 5x > 5x - 5x + 6 [नियम (ii) के अनुसार]
या \(\frac{-2 x}{-2}<\frac{6}{-2}\) [नियम (iv) के अनुसार ]
या x < 3
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ ( - ∞, - 3 ) उत्तर

प्रश्न 7. 
3(x - 1) < 2 (x - 3)
हल:
प्रश्नानुसार 3(x - 1 ) < 2 (x - 3)
3x - 3 < 2x - 6
3x - 3 + 3 < 2x - 6 + 3 [नियम (i) के अनुसार] 
या 3x < 2x - 3
या 3x - 2x < 2x - 2x - 3 [ नियम (ii) के अनुसार ]
या x ≤ - 3 .....(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (-∞, -3]

प्रश्न 8.
3 (2 - x) ≥ 2 (1 - x)
हल:
प्रश्नानुसार 3 (2 - x) ≥ 2 (1 - x)
या 6 - 3x ≥ 2 - 2x
या 6 - 3x + 3x ≥ 2 - 2x + 3x [नियम (i) के अनुसार ] 
या 6 ≥ 2 + x
या 6 - 2 ≥ 2 + x - 2 [ नियम (ii) के अनुसार ]
या 4 ≤ x
या x ≤ 4 ...........(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (∞, 4]

प्रश्न 9. 
x + \(\frac{x}{2}+\frac{x}{3}\) < 11
हल:
प्रश्नानुसार x + \(\frac{x}{2}+\frac{x}{3}\) < 11
या 6[x + \(\frac{x}{2}+\frac{x}{3}\)] < 11 × 6
(2 या 3 के ल.स. का दोनों पक्षों में गुणा करने पर)
या 6x + 3x + 2x < 66
या 11x < 66
या \(\frac{11 x}{11}<\frac{66}{11}\) [नियम (iii) के अनुसार ]
या x < 6 ...(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (-∞, 6)

प्रश्न 10.
\(\frac{x}{3}>\frac{x}{2}\) + 1
हल:
प्रश्नानुसार \(\frac{x}{3}>\frac{x}{2}\) + 1
दोनों पक्षों में 6 का गुणा करने पर
या 6 × \(\frac{x}{3}\) > 6 (\(\frac{x}{2}\) + 1 )
या 2x > 3x + 6
या 2x - 3x > 3x + 6 - 3x [ नियम (ii) के अनुसार ]
या - x > 6
या x < - 6 [नियम (iv) के अनुसार] ....(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (−∞, −6)

प्रश्न 11.
\(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
हल:
प्रश्नानुसार \(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
दोनों पक्षों में 15 का गुणा करने पर
15\(\left[\frac{3(x-2)}{5}\right]\) ≤ 15\(\left[\frac{5(2-x)}{3}\right]\)
या 9 (x-2) ≤ 25 (2 − x)
या 9x - 18 < 50 - 25x
या 9x - 18 + 18 < 50 - 25x + 18 [नियम (i) के अनुसार ]
या 9x < 68 - 25x
या 9x + 25x< 68 - 25x + 25x [नियम (i) के अनुसार ]
या 34x < 68
या \(\frac{34 x}{34} \leq \frac{68}{34}\) [नियम (iii) के अनुसार ]
या x ≤ 2 ..(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (−∞, 2]

प्रश्न 12.
\(\frac{1}{2}(\frac{3 x}{5} + 4) ≥ \frac{1}{3}\)
हल:
प्रश्नानुसार

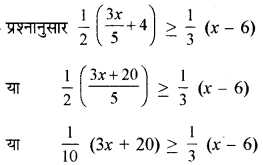
दोनों पक्षों में 30 से गुणा करने पर
\(\frac{30}{10}\)(3x + 20) > \(\frac{30}{10}\)(x - 6)
या 3 (3x + 20) ≥ 10 (x - 6)
या 9x + 60 ≥ 10x - 60
या 9x + 60 - 60 ≥ 10x - 60 - 60 [नियम (ii) के अनुसार ]
या 9x > 10x - 120
या 9x - 10x ≥ 10x - 120 - 10x [नियम (ii) के अनुसार ]
या - x ≥ - 120
या x ≤ 120 [नियम (iv) के अनुसार] ................(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (-∞, 120]

प्रश्न 13. 
2 (2x + 3) - 10 < 6 (x − 2)
हल:
प्रश्नानुसार 2 (2x + 3 ) - 10 < 6 (x - 2)
या 4x + 6 - 10 < 6x - 12
या 4x - 4 < 6x - 12
या 4x - 4 + 12 < 6x - 12 + 12 [नियम (i) के अनुसार]
या 4x + 8 < 6x
या 4x - 4x + 8 < 6x - 4x [नियम (ii) के अनुसार]
या 8 < 2x
या 2x > 8
या x > 4 [नियम (iii) के अनुसार] .....(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (4, 0)

प्रश्न 14.
37 - (3x + 5) ≥ 9x - 8 (x - 3)
हल:
प्रश्नानुसार 37 - (3x + 5) ≥ 9x - 8 (x - 3)
या 37 - 3x - 5 ≥ 9x - 8x + 24
या 32 - 3x ≤ x + 24
या 32 - 3x + 3x≤ x + 24 + 3x [ नियम (i) के अनुसार ]
या 32 > 4x + 24
या 32 - 24 > 4x + 24 - 24 [ नियम (ii) के अनुसार ]
या 4x < 8
या \(\frac{4 x}{4} \leq \frac{8}{4}\) [नियम (iii) के अनुसार ]
या x < 2 ...........(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (0, 2]

प्रश्न 15.
\(\frac{x}{4}<\frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
हल:
प्रश्नानुसार \(\frac{x}{4}<\frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
दोनों पक्षों में 3, 4 व 5 के ल.स. 60 का गुणा करने पर
या 15x < 20 (5x - 2) - 12 (7x - 3)
या 15x < 100x - 40 - 84x + 36
या 15x < 16x - 4
या 15x + 4 < 16x – 4 + 4 [नियम (i) के अनुसार] 
या 15x + 4 < 16x
या 15x – 15x + 4 < 16x - 15x [नियम (ii) के अनुसार]
या 4 < x
या x > 4 .......(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (4, ∞)

प्रश्न 16.
\(\frac{(2 x-1)}{3} \geq \frac{(3 x-2)}{4}-\frac{(2-x)}{5}\)
हल:
प्रश्नानुसार \(\frac{(2 x-1)}{3} \geq \frac{(3 x-2)}{4}-\frac{(2-x)}{5}\)
दोनों पक्षों में 3, 4 व 5 के ल.स. 60 का गुणा करने पर
60\(\left[\frac{2 x-1}{3}\right]\) ≥ 60 \(\left[\frac{3 x-2}{4}-\frac{2-x}{5}\right]\)
या 20 (2x - 1) ≥ 15 (3x - 2 ) - 12 (2 - x)
या 40x - 20 ≥ 45x - 30 - 24 + 12x
या 40x - 20 > 57x - 54
या 40x - 20 + 20 > 57x - 54 + 20 [नियम (i) के अनुसार]
या 40x > 57x - 34
या 40x - 57x ≥ 57x - 57x - 34 [नियम (ii) के अनुसार]
या - 17x > - 34
या \(\frac{-17 x}{-17} \leq \frac{-34}{-17}\) [नियम (iv) के अनुसार]
या x ≤ 2 .... (i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (0, 2]

प्रश्न 17 से 20 तक की असमिकाओं का हल ज्ञात कीजिए तथा उन्हें संख्या रेखा पर आलेखित कीजिए ।

प्रश्न 17. 
3x - 2 < 2x + 1
हल:
प्रश्नानुसार 3x - 2 < 2x + 1
या 3x - 2 + 2 < 2x + 1 + 2
या 3x < 2x + 3
या 3x - 2x < 2x + 3 - 2x
या x < 3 .............(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (-∞, 3)

संख्या रेखा पर आलेख

प्रश्न 18.
5x - 3 ≥ 3x - 5
हल:
प्रश्नानुसार 5x - 3 ≥3x - 5
या 5x - 3 + 3 ≥ 3x - 5 + 3 [ नियम (i) के अनुसार ]
या 5x ≥ 3x - 2
या 5x - 3x ≥ 3x - 2 - 3x
या 2x ≥ - 2
या \(\frac{2 x}{2} \geq \frac{-2}{2}\)
या x ≥ -1 .............(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ [-1, ∞) 
अर्थात् समस्त वास्तविक संख्याएँ x या तो बराबर या - 1 से बड़ी संख्याएँ होंगी ।
संख्या रेखा पर आलेख

प्रश्न 19.
3 (1 - x) < 2 (x + 4)
हल:
प्रश्नानुसार 3 (1 - x) < 2 (x + 4 )
या 3 - 3x < 2x + 8
या 3 - 3x - 3 < 2x + 8 - 3
या - 3x - 2x < 2x + 5 - 2x
या 5x < 5
या - 3x < 2x + 5
या \(\frac{-5 x}{-5}>\frac{5}{-5}\) [नियम (iv) के अनुसार ]
या x > -1
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ (- 1, ∞)
अर्थात् समस्त वास्तविक संख्याएँ x, -1 से बड़ी संख्या होंगी । संख्या रेखा पर आलेख

प्रश्न 20.
\(\frac{x}{2} \geq \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
हल:
प्रश्नानुसार \(\frac{x}{2} \geq \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
दोनों पक्षों में 2, 3, 5 के ल.स. 30 का गुणा करने पर
या 30() >30
या 15x ≥ 10 (5x - 2) - 6 (7x - 3)
या 15x ≥ 50x - 20 - 42x + 18
या 15x ≥ 8x - 2
या 15x - 8x ≥ 8x - 2 - 8x
या 7x ≥ - 2
या x ≥ 7 ..............(i)
अतः असमिका (i) से अभीष्ट असमिका का हल, x ∈ [\(\frac{-2}{7}\), ∞)
संख्या रेखा पर आलेख
अर्थात् समस्त वास्तविक संख्याएँ x = \(\frac{-2}{7}\) से बड़ी होंगी-

प्रश्न 21.
रवि ने पहली दो एकक परीक्षा में 70 और 75 अंक प्राप्त किए हैं । वह न्यूनतम अंक ज्ञात कीजिए, जिसे वह तीसरी एकक परीक्षा में पाकर 60 अंक का न्यूनतम औसत प्राप्त कर सके ।
हल:
माना कि रवि ने तीसरी एकक परीक्षा में x अंक प्राप्त किए।
∴ रवि के द्वारा प्राप्त अंकों का औसत = \(\frac{70+75+x}{3}\)
लेकिन चूँकि उसे औसतन 60 अंक प्राप्त करने हैं अतः
\(\frac{70+75+x}{3}\) ≥ 60
या \(\frac{145+x}{3}\) ≥ 60
दोनों पक्षों को 3 से गुणा करने पर
145 + x ≥ 180
या x ≥ 180 - 145
या x ≥ 35
अर्थात् रवि को तीसरी एकक परीक्षा में 35 अंक या उससे अधिक अंक प्राप्त करने होंगे ।

प्रश्न 22.
किसी पाठ्यक्रम में ग्रेड 'A' पाने के लिए एक व्यक्ति को सभी पाँच परीक्षाओं (प्रत्येक 100 में से ) में 90 अंक या अधिक अंक का औसत प्राप्त करना चाहिए। यदि सुनीता के प्रथम चार परीक्षाओं के प्राप्तांक 87, 92, 94 और 95 हों तो वह न्यूनतम अंक ज्ञात कीजिए जिसे पाँचवीं परीक्षा में प्राप्त करके सुनीता उस पाठ्यक्रम में ग्रेड 'A' पाएगी।
हल:
माना कि सुनीता ने पाँचवीं परीक्षा में x अंक प्राप्त किए । अतः पाँच परीक्षाओं के प्राप्तांकों का औसत
= \(\frac{87+92+94+95+x}{5}=\frac{368+x}{5}\)
प्रश्नानुसार यह औसत कम से कम 90 होना चाहिए ।
अर्थात् \(\frac{368+x}{5}\) ≥ 90
दोनों पक्षों को 5 से गुणा करने पर
368 + x ≥ 5 × 90
या 368 + x ≥ 450
या 368 + x - 368 ≥ 450 - 368
या x ≥ 82
अर्थात् सुनीता को पाँचवीं परीक्षा में 82 या इससे अधिक अंक प्राप्त करने चाहिए ।

प्रश्न 23.
10 से कम क्रमागत विषम संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनके योगफल 11 से अधिक हों ।
हल:
माना कि x और x + 2 दो विषम प्राकृत संख्याएँ हैं । x तथा x + 2 दोनों ही संख्याएँ 10 से कम हैं । अर्थात्
x < 10 ............(i) 
तथा x + (x + 2) > 11
असमिका (ii) से x + x + 2 > 11
या 2x + 2 > 11
या x > \(\frac{9}{2}\) .......(ii)
अब असमिका (i) व (iii) से
\(\frac{9}{2}\) < x < 10
या 4.5 < x < 10
अर्थात् ये विषम संख्याएँ x 4.5 तथा 10 के मध्य होनी चाहिए । अतः इन संख्याओं का युग्म (5, 7) तथा (7, 9) होगा ।

प्रश्न 24.
क्रमागत सम संख्याओं के ऐसे युग्म ज्ञात कीजिए, जिनमें से प्रत्येक 5 से बड़े हों, तथा उनका योगफल 23 से कम हो ।
हल:
माना कि x और x + 2 दो सम संख्याएँ हैं । x तथा x + 2 दोनों ही 5 से बड़ी सख्याएँ हैं ।
अर्थात् x > 5 ..............(i)
तथा x + x + 2. < 23 ..........(ii)
असमिका (ii) को हल करने पर 2x + 2 < 23
या 2x + 2 - 2 < 23 - 2
या 2x < 21
या x < \(\frac{21}{2}\) ...............(iii)
अब असमिकाओं (i) तथा (iii) से
या 5 < x < \(\frac{21}{2}\)
5 < x < 10.5
अर्थात् ये सम संख्याएँ x, 5 तथा 10.5 के मध्य होंगी ।
अतः ऐसी वांछित संख्याओं का युग्म (6, 8), (8, 10) तथा (10, 12) होगा।

प्रश्न 25. 
एक त्रिभुज की सबसे बड़ी भुजा सबसे छोटी भुजा की तीन गुनी है तथा त्रिभुज की तीसरी भुजा सबसे बड़ी भुजा से 2 सेमी. है । तीसरी भुजा की न्यूनतम लम्बाई ज्ञात कीजिए जबकि त्रिभुज का परिमाप न्यूनतम 61 सेमी. है 1
हल:
माना कि त्रिभुज की सबसे छोटी भुजा x है ।
∴ सबसे बड़ी भुजा = 3x
तथा तीसरी भुजा = 3x - 2 
प्रश्न में दी गई शर्त के अनुसार
x + 3x + (3x - 2) > 61
या 7x - 2 ≥ 61
या 7x - 2 + 2 ≥ 61 + 2
या 7x ≥ 63
या x > 9
अर्थात् सबसे छोटी भुजा 9 सेमी. है

प्रश्न 26.
एक व्यक्ति 91 सेमी. लम्बे बोर्ड में से तीन लम्बाइयाँ काटना चाहता है । दूसरी लम्बाई सबसे छोटी लम्बाई से 3 सेमी. अधिक और तीसरी लम्बाई सबसे छोटी लम्बाई की दुगुनी है। सबसे छोटे बोर्ड की सम्भावित लम्बाइयाँ क्या हैं, यदि तीसरा टुकड़ा दूसरे टुकड़े से कम से कम 5 सेमी. अधिक लम्बा हो ?
[संकेत : यदि सबसे छोटे बोर्ड की लम्बाई x सेमी. हो, तब (x + 3) सेमी. और 2x सेमी. क्रमश: दूसरे और तीसरे टुकड़ों की लम्बाइयाँ हैं । इस प्रकार x + (x + 3 ) + 2x ≤ 91 और
2x ≤ (x + 3) + 5]
हल:
माना कि सबसे छोटे कटे बोर्ड की लम्बाई = x सेमी.
दूसरे कटे बोर्ड की लम्बाई = x + 3 सेमी.
तथा तीसरे कटे बोर्ड की लम्बाई = 2x सेमी.
अतः x + (x + 3) + 2x ≤ 91
तथा 2x ≥ (x + 3) + 5 ........ (ii)
असमिका (i) को हल करने पर 4x + 3 ≤ 91
या 4x + 3 - 3 ≤ 91 - 3
या 4x ≤ 88
या x ≤ 22
(iii)
असमिका (ii) को हल करने पर
या 2x ≥ 2x + 8
x ≥ 8
असमिकाओं (iii) व (iv) के आधार पर यह कहा जा सकता है कि x का मान 8 तथा 22 के मध्य है अर्थात्
8 ≤ x ≤ 22
अतः सबसे छोटे बोर्ड की सम्भावित लम्बाई 8 सेमी. से बड़ी या 8 के बराबर किन्तु 22 सेमी. से कम या इसके बराबर है।