RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 6 Linear Inequalities Ex 6.1

Question 1.
Solve : 24.x < 100, when :
(i) x is a natural number,
(ii) x is an integer.
Answer:
Given inequality:
24x < 100
\(\frac{24 x}{24}<\frac{100}{24}\)
⇒ x < \(\frac{100}{24}\) (Dividing both sides by 24)
or x < \(\frac{25}{6}\) ⇒ x < 4\(\frac{1}{6}\)

(i) When x is a natural number, then
For x = 1, 2, 3, 4 x < \(\frac{25}{6}\) is true
For x = 1, 1 < \(\frac{25}{6}\) is true
Similarly
For x = 2, 2 < \(\frac{25}{6}\) is true
For x = 3, 3 < \(\frac{25}{6}\) is true
For x = 4, 4 < \(\frac{25}{6}\) is true
Thus, solution of inequality are 1, 2, 3, 4
Solution set is {1, 2, 3, 4}

(ii) x < \(\frac{25}{6}\) When x is an integer, in this case solutions of inequality will be all integers less than \(\frac{25}{6}\). Thus, - ∞ ............. - 3, - 2 -1, 0,1, 2, 3, 4........... are solutions of inequality. Solution set = {.... -3, -2, -1, 0, 1, 2, 3, 4} Question 2. Solve: - 12x > 30, when
(i) x is a natural number,
(ii) x is an integer.
Answer:
(i) Given inequality : -12x > 30
Multiplying both sides by (-1)
(-1) × (-12) x < (-1) × (30) [When multiply by -1, sign '>’ converts into ‘<’ ]
or 12x < -30
or x < \(\frac{-30}{12}\) (Dividing both sides by 12)
or x < \(\frac{-5}{2}\)
We know that no natural number is negative or less than \(\frac{-5}{2}\)
Thus, there is no solution in set of a natural numbers of given inequality.

(ii) Again, when x is an integer, then solution of inequality will be ∞, ........ -5, - 4, - 3.
Since, - 3< \(\frac{-5}{2}\), -4<  \(\frac{-5}{2}\)
Thus, solution set = {...., -5, -4, -3}

 

Question 3.
Solve : 5x - 3 < 7, when
(i) x is an integer,
(ii) x is a real number.
Answer:
Given inequality: 5x - 3 < 7
Adding 3 on both sides,
5x < 7 + 3
or 5x < 10
or \(\frac{5 x}{5}<\frac{10}{5}\) (Dividing both sides by 5)
or x < 2

(i) When x is an integer then solution of inequality are integers which are smaller then 2 i.e.- 3, - 2, - 1, 0, 1
Solution set = {-∞,... -3, -2, -1, 0, 1}

(ii) Again 5x - 3 < 7
or 5x < 7 + 3
or 5x < 10
or x < \(\frac{10}{5}\)
or x< 2 When x is a real number then solution of inequality will be all real numbers less than 2. Thus, solution set is = (- ∞, 2) Question 4. Solve 3x + 8 > 2, when
(i) x is an integer,
(ii) x is a real number.
Answer:
Given inequality : 3x + 8 > 2
or 3x > 2 - 8
(Subtracting 8 from both sides)
or 3x > - 6
or x > \(-\frac{6}{3}\)
or x > - 2

(i) When x is an integer, then all integers greater than - 2 will be solution of inequality i.e. solutions are -1, 0, 1, 2,3, ......................ui. and solution set is = [-1, 0,1, 2, 3, ..................]

(ii) When x is a real number then solution of inequality x > - 2 will be all real numbers greater than - 2

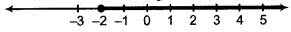
Thus, solution set will be = (-2, ∞)

Solve the inequalities in exercise 5 to 16 for real x.

Question 5.
4x + 3 < 5x + 7
Answer:
Given inequality : 4x + 3 < 5x + 7
∴ 4x + 3 < 5x + 7
or 4x < 5x + 7 - 3
(Subtracting 3 from both sides)
4x < 5x + 4
or 4x - 5x < 4 (Subtracting 6x from both sides)
or - x < 4 Multiplying both sides by (-1) (-1) × (- x) > (- 1) × (4)
(After mutiplying by - 1 < sign converts into > sign)
or x > - 4
When x is real number, then solution of inequality is all real numbers greater than - 2

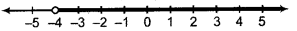
Thus, solution set = (- 2, ∞)

Question 6.
3x - 7 > 5x - 1
Answer:
Given inequality : 3x -1 > 5x - 1
3x - 7 > 5x - 1
or 3x > 5x - 1 + 7 (Adding 7 on both sides)
or 3x > 5x + 6
or 3x - 5x > 6 (Subtracting 5x from both sides)
or -2x > 6,
Mutliplying both sides by (-1),
(-1) × (- 2x) < (-1) × (6) (Mutliplying by -1, sign > converts into <)
or 2x < - 6
or x < - 3
Thus, solution of inequality will be all real numbers less than - 3.

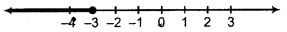
Thus, solution set = (-∞, - 3)

Question 7.
3 (x - 1)< 2 (x - 3)
Answer:
Given inequality : 3 (x -1) ≤ 2 (x - 3)
.-. 3 (x - 1) < 2 (x - 3)
or 3x - 3 ≤ 2x - 6 (Adding 3 on both sides)
or 3x ≤ 2x - 6 + 3
or 3x ≤ 2x - 3
or 3x - 2x ≤ - 3 (Subtracting 2x from both sides)
or x ≤ -3
Thus, solution of given inequality will be all real numbers equal to - 3 or less than - 3
Thus, solution set = (-∞, - 3]

Question 8.
3(2 - x) ≥ 2(1 - x)
Answer:
Given inequality : 3 (2 - x) ≥ 2 (1 - x)
3 (2 - x) ≥ 2 (1 - x)
6 - 3x ≥ 2 - 2x
or - 3x ≥ 2 - 2x - 6
(Subtracting 6 from both sides)
or - 3x ≥ - 2x - 4
or - 3x + 2x ≥ - 4 (Adding 2x in both sides)
or - x ≥ - 4
Multiplying both sides by (- 1)
(-1) × (-x) ≤ (-4) × (-1)
[Multiplying by (- 1), sign ≥ converts into<]
or x < 4

Thus, solution of given inequality will be all real numbers which are equal to or less 4.
Thus, solution set = (-∞, 4]

Question 9.
x + \(\frac{x}{2}+\frac{x}{3}\) < 11
Answer:
Given inequality : x + \(\frac{x}{2}+\frac{x}{3}\) < 11
x + \(\frac{x}{2}+\frac{x}{3}\) < 11
or \(\frac{6 x+3 x+2 x}{6}\) < 11
or 11x < 11 × 6 (Multiplying both sides by 6)
or 11x < 66
or x < \(\frac{66}{11}\) (Dividing both sides by 11)
or x< 6 Thus, solution of given inequality will be all real numbers less than 6

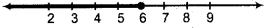
Thus, solution set = (-∞, 6)

Question 10.
\(​​​​​​​\frac{x}{3}>\frac{x}{2}\) + 1
Answer:
Given inequality : \(​​​​​​​\frac{x}{3}>\frac{x}{2}\) + 1
Thus \(​​​​​​​\frac{x}{3}>\frac{x}{2}\) + 1
(Subtracting \(\frac{x}{2}\) from both sides)
Thus \(\frac{x}{3}-\frac{x}{2}\) > 1
or \(\frac{2 x-3 x}{6}\) > 1
or \(\frac{-x}{6}\) > 1
or -x > 6
(Multiplying both sides by 6) Multiplying both sides by (- 1)
(-1) × (- x) < (-1) × (6) (Multiplying by - 1 sign > converts into < sign)

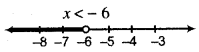
Thus, all real numbers less than - 6 are solution of given inequality. Thus, solution set = (-∞,- 6)

Question 11.
\(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
Answer:
Given inequality : \(\frac{3(x-2)}{5} \leq \frac{5(2-x)}{3}\)
or \(\frac{(3 x-6)}{5} \leq \frac{10-5 x}{3} \)
or 3 (3A - 6) ≤ 5 (10 - 5A) (By cross-multiplication)
or 9x -18 ≤ 50 - 25x
or 9A ≤ 50 - 25x + 18 (Adding 18 in both sides)
or 9x + 25.x ≤ 68 (Adding 25 x in both sides)
or 34x ≤ 68
or x ≤ \(\frac{68}{34}\)
or x ≤ 2
Thus, all real numbers equal to or less than 2 are solution of given inequality.

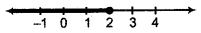
Thus, solution set will be = (-∞, 2]

Question 12.
\(\frac{1}{2}\left(\frac{3 x}{5}+4\right) \geq \frac{1}{3}\)(x - 6)
Answer:
Given inequality: \(\frac{1}{2}\left(\frac{3 x}{5}+4\right) \geq \frac{1}{3}\)(x-6)
or \(\frac{1}{2}\left(\frac{3 x+20}{5}\right) \geq \frac{(x-6)}{3}\)
or \(\frac{(3 x+20)}{10} \geq \frac{(x-6)}{3}\)
or 3 (3x + 20) ≥ 10 (x - 6) (By cross-multiplication) 
or 9x + 60 ≥ 10x - 60
or 9x ≥ 10x - 60 - 60 (Subtracting 60 from both sides)
or 9x ≥ 10x - 120
or 9x - 10x ≥ -120 (Subtracting 10A from both sides)
or -x ≥ -120
Multiplying (- 1) on both sides,
(-1) × (- x) ≤ (- 1) × (-120)
(Multiplying by (-1) sign > converts into <)
or x ≤ 120

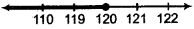
Thus, all real numbers equal to or less than 120 are solution of given inequality.
Thus, solution set = (- ∞, 120]

Question 13.
2 (2x + 3) - 10 ≤ 6 (x - 2)
Answer:
Given inequality:
2(2x + 3) - 10 ≤ 6 (x - 2)
Now, 2(2x + 3) -10 ≤ 6(x - 2)
or 4x + 6 - 10 ≤ 6x - 12
or 4x - 4 ≤ 6x - 12
or 4x ≤ 6x - 12 + 4 (Adding 4 on both sides)
or 4x ≤ 6x - 8
or 4x - 6x ≤ - 8
(Subtracting 6A from both sides)
or - 2x ≤ - 8
Multiplying both sides by
(- 1) (-1) × (- 2x) ≥ (-1) × (- 8)
or 2x ≥ 8 (sign < converts into >)
or x ≥ 4

Thus, all real numbers greater than 4 are solution of given inequaltiy.
Thus, solution set = (4, ∞)

Question 14.
37 - (3x + 5) ≥ 9x - 8 (x - 3)
Answer:
Given inequality:
37 - (3x + 5) ≥ 9A - 8 (x - 3)
Thus 37 - (3x + 5) ≥ 9x - 8 (x - 3)
or 37 - 3x - 5 ≥ 9x - 8x + 24
or 32 - 3x ≥ x + 24
or -3x ≥ x + 24 - 32 (Subtracting 32 from both sides)
or - 3x ≥ x - 8
or - 3x - x ≥ - 8
(Subtracting x from both sides)
or - 4x ≥ - 8
or -x ≥ -2
Multiplying both sides by (- 1),
(-1) × (-x) ≤ (-1) × (- 2)
[Multiplying by (- 1) sign > converts into <]

All real numbers equal to or less than 2 are solution of given inequality.
Thus, solution set = (- ∞, 2]

Question 15.
\(\frac{x}{4}<\frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
Answer:
Given inequality \(\frac{x}{4}<\frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}\)
or \(\frac{x}{4}<\frac{25 x-10-21 x+9}{15}\)
or \(\frac{x}{4}<\frac{(4 x-1)}{15}\)
or 15x < 16x - 4 (By cross-multiplication)
or 15 x < 1 6x - 4
or 15x - 16x < - 4
(Subtracting 16 x from both sides)
or - x < - 4 Multiplying (- 1) on both sides, (-1) × (- x) > (-1) × (- 4)
(Multiplying by (-1), sign < converts into >)
or x > 4

Thus, solution of given inequality will be all real numbers which are greater than 4.
Thus, solution set will be (4, ∞)

Question 16.
\(\frac{(2 x-1)}{3} \geq \frac{(3 x-2)}{4}-\frac{(2-x)}{5}\)
Answer:
We have \(\frac{(2 x-1)}{3} \geq \frac{(3 x-2)}{4}-\frac{(2-x)}{5}\)
Thus \(\left(\frac{2 x-1}{3}\right) \geq \frac{15 x-10-8+4 x}{20}\)
or \(\frac{2 x-1}{3} \geq \frac{19 x-18}{20}\)
or 20 (2x-1) ≥ 3 (19x - 18)
(By cross-multiplication)
or 40x - 20 ≥ 57x - 54
or 40x ≥ 57x -54 + 20 (Adding 20 in both sides)
or 40x ≥ 57x - 34 (Subtracting 57x from both sides)
or 40x - 57x ≥ - 34
or -17x ≥ -34 Multiplying both sides-by (-1)
(-1) × (-17x) ≤ (-1) × (- 34)
or 17x ≤ 34
(Multiplying by (-1), > sign converts into <)
x ≤ 2

Thus, solution of given inequality will be all real numbers which are equal to or less than 2.
Thus, solution set will be (-∞ 2].

Solve the inequalities in exercise 17 to 20 and show the graph of the solution in each case on number line.

Question 17.
3x - 2 < 2x + 1
Answer:
Given : 3x - 2 < 2x +1
Thus 3x - 2 < 2x +1 .
or 3x < 2x + 1 + 2 (Adding 2 on both sides)
or 3x < 2x + 3
or 3x - 2x < 3 (Subtracting 2x from both sides)
Thus, solution of given inequality are all real numbers which are less than 3.
Thus, solution set = (- ∞, 3)
or x < 3

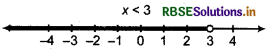
x < 3 can be graphically represent on numbers line as 3 is not included.

Question 18.
5x - 3 ≥ 3x - 5
Answer:
We have, 5x - 3 ≥ 3x - 5
Thus 5x - 3 ≥ 3x - 5
or 5x ≥ 3x - 5 + 3 (Adding 3 on both sides)
or 5x ≥ 3x - 2
or 5x - 3x ≥ - 2 (Subtracting 3x from both sides)
or 2x ≥ - 2
or x ≥ -1 (Dividing both sides by 2)
Thus, solution of given inequality are all real numbers which are equal to - 1 or greater than - 1.
Thus, solution of inequality x = [-1, ∞)
x ≥ -1 can be represented graphically on number line

(- 1) is included.

Question 19.
3(1 - x) < 2(x + 4)
Answer:
We have ;3 (1 - x) < 2 (x + 4)
Thus 3 (1 - x) < 2 (x + 4)
or 3 - 3x < 2x + 8
or -3x < 2x + 8 - 3 (Subtracting 3 from both sides)
or -3x < 2x + 5
or -3x - 2x < 5 (Subtracting 2 from both sides)
or -5x < 5
or -x < 1 Multiplying both sides by ( 1) (-1) × (- x) > (-1) × (1)
or x > -1
(By multiplying -1 )
Thus, all the real numbers greater than - 1 are solution of inequality.
Thus, solution of inequality : x = (-1, ∞)
On number line x > -1 can be represented by

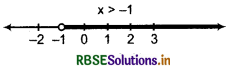
-1 is not included

Question 20.
\(\frac{x}{2} \geq \frac{5 x-2}{3}-\frac{(7 x-3)}{5}\)
Answer:
We have: \(\frac{x}{2} \geq \frac{5 x-2}{3}-\frac{(7 x-3)}{5}\)
or \(\frac{x}{2} \geq \frac{25 x-10-21 x+9}{15}\)
or \(\frac{x}{2} \geq \frac{4 x-1}{15}\)
or 15x ≥ 8x - 2 (By cross-multiplication)
.or 15x - 8x ≥ -2
or 7x ≥ -2
or x ≥ \(-\frac{2}{7}\) (Dividing both sides by 7)
All real numbers greater than or equal to \(-\frac{2}{7}\) are solution of given inequality.
Thus, solution of inequality:
x = [ \(-\frac{2}{7}\), ∞)
x ≥ \(-\frac{2}{7}\) can be represented on number line as follows :

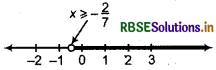
\(-\frac{2}{7}\) is not included.

Question 21.
Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
Answer:
Let Ravi got x marks in third exams.
Thus, average marks of three exams.
= \(\frac{70+75+x}{3}\)
Then, \(\frac{70+75+x}{3}\) ≥ 60
or 145 + x ≥ 180 (By cross-multiplication)
or x ≥ 180 - 145
or x ≥ 35 (Subtracting 145 from both sides)
Thus, Ravi should got minimum 35 or more marks in third exams.
Equal to or more than 35.

Question 22.
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get Grade ‘A’ in the course.
Answer:
Let Sunita got x marks in fifth exams
Thus, average marks of five exams = \(\frac{87+92+94+95+x}{5}\)

Then, according to question to get ‘A’ Grade
= \(\frac{87+92+94+95+x}{5}\) ≥ 90
or \(\frac{368+x}{5}\) ≥ 90
or (368 + x) ≥ 90 × 5 (By cross-multiplication)
or 368 + x ≥ 450
or x ≥ 450 - 368 (Subtracting 368 from both sides)
or x ≥ 82
Thus, to obtain Grade ‘A’ in fifth exams, Sunita should get 82 or mork marks.

Question 23.
Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
Answer:
Let x and (x + 2) are two consecutive odd numbers.
(Difference of two consecutive odd numbers is 2)
x< 10 ...(1) We have, x + x + 2 > 11
or 2x + 2 >11 ...(2)
or 2x > 11 - 2
or 2x > 9
or x > \(\frac{9}{2}\)
From (1) and (3), It concludes that
\(\frac{9}{2}\) < x < 10 or 4.5 < x < 10 Thus, required values of odd number x lies between \(\frac{9}{2}\) and 10. Thus, all possible pair will be (5,7), (7,9). Question 24. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23. Answer: Let two consecutive even numbers are x and x + 2. (Since, difference of two consecutive even numbers is 2) We have, x > 5 ...(1)
x + x + 2 < 23 ...(2)
or 2x + 2< 23
or 2x < 23 - 2
or 2x < 21
or x < \(\frac{21}{2}\) ...(3)
From (1) and (3), it concludes that
5 < x < \(\frac{21}{2}\)
or 5 < x < 10.5
Thus, required value of even number x lies between 5 21 and \(\frac{21}{2}\). So all possible pairs will be (6, 8), (8, 10) and (10,
12). Since6 + 8 < 23, 8 + 10 < 23, 10 + 12 < 23)

Question 25.
The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
Answer:
Let length of third side be x cm We have
Length of longest side = (x + 2) cm
and length of smallest side = - (x + 2) cm
Then, sides of triangle \(\frac{x+2}{3}\), x, x + 2
Thus, perimeter of triangle = \(\left(\frac{x+2}{3}\right)\) + x + (x + 2)

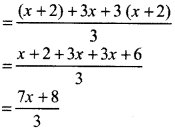
In question, perimeter of triangle is minimum 61 cm i.e., perimeter is 61 or more than 61.
Then, \(\frac{7 x+8}{3}\) ≥ 61
or 7x + 8 ≥ 183 (By cross-multiplication)
or 7x ≥ 183 - 8 (Subtracting 8 from both sides)
or 7x ≥ 175
or x ≥ \(\frac{175}{7}\) (Dividing both sides by 7)
or x ≥ 25
Thus, length of third side should be at least 25 cm or more than it.

Question 26.
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm. Longer than the shortest and the third length is to be twice as long as the shortest What are the possible lengths of the shortest board, if the third piece is to be at least 5 cm longer than the second?
Answer:
If x is the length of the shortest board, then (x + 3) and 2x are the lengths of the second and third piece, respectively.
We have, x + (x + 3) + 2x ≤ 91
or 4x + 3 ≤ 91
or 4x ≤ 91 - 3 (subtracting 3 from both sides)
or 4x ≤ 88
or x ≤ 22 cm (Dividing both sides by 4)
But according to question length of third board is at least 5 cm more than second.
Thus, 2x ≥ (x + 3) + 5
or 2x - x ≥ 8 (Subtracting x from both sides)
or x ≥ 8
Since, x ≥ 8 and x ≤ 22
Thus, 8 ≤ x ≤ 22
It means x is equal to 8 or more than 8 and equal to or less than 22.
Thus, possible lengths of the shortest board is minimum 8 cm. and maximum 22 cm.