RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise

Question 1.
Evaluate \(\left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^3\).
Answer:

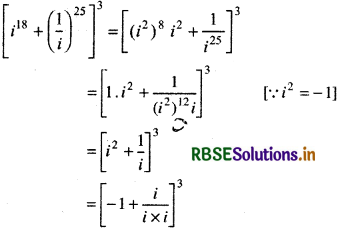
(Multiplying numerator and denominator by i in second term).
= [- 1 + \(\frac{i}{i^2}\)]³
= [- 1 - i]³ (∵ i² = - 1)
= - [1 + i]³
=- [1 + 3i + 3i² + i³]
[By expansion of(1 + i)³]
= - [1 + 3i - 3 + i² . i]
= - [1 + 3i - 3 - 1 × i]
= - [- 2 + 3i - i]
= - [- 2 + 2i]
= 2 - 2i
Thus, \(\left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^3\) = 2 - 2i

Question 2.
For any two complex numbers z₁ and z₂, show that:
Re(z₁z₂) = Rez₁ Rez₂ - Imz₁ Imz₂
Answer:
Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂
then z₁z₂ = (x₁ + iy₁) (x₂ + iy₂)
= (x₁x₂ + ix₁y₂ + iy₁x₂ + i²y₁y₂
= x₁x₂ + i(x₁y₂ + x₂y₁) - y₂y₁ (∵ i² = - 1)
= (x₁x₂ - y₁y₂) + i(x₁y₂ + x₂y₁)
Then, real value of z₁ z₂
L.H.S Re(z₁z₂) = (x₁x₂ - y₁y₂) .............. (1)
(Since here i does not exist)
Again, Rez₁, Rez₂ - Imz₁ Imz₂
Real z₁ (Rez₁) = x₁ (z₁ = x₁ + iy₁)
and real z₂,(Rez₂) = x₂ (z₂ = x₂ + iy₂) .
and imaginary z₁, (Im z₁) = y₁ (z₁ = x₁ + iy₁)
and imaginary z₂(Imz₂) = y₂ (z₂ = x₂ + iy₂)
and (Rez₁) Re(z₂) - (Imz₁) (Imz₂)
= x₁x₂ - y₁y₂
= Re (z₁z₂) [From equation (I)]
Thus Re(z₁z₂) = (Rez₁) (Rez₂) - (Im z₁) (Im z₂)
Hence proved

Question 3.
Reduce \(\left(\frac{1}{1-4 i}-\frac{2}{1+i}\right)\left(\frac{3-4 i}{5+i}\right)\) to the standard form.
Answer:

Second Method:

Question 4.
If x - iy = \(\sqrt{\frac{a-i b}{c-i d}}\), prove that (x² + y²)² = \(\frac{a^2+b^2}{c^2+d^2}\).
Answer:

Question 5.
Convert the following into polar form:
(i) \(\frac{1+7 i}{(2-i)^2}\)
Answer:

Which will be represent in second quadrant.
Since in second quadrant X-axis is +ve and Y-axis is -ve.
Then, given expression = \(\frac{1+7 i}{(2-i)^2}\) = - 1 + i.
Let - 1 + i = r(cos θ + i sin θ)
⇒ - 1 + i = r cos θ + i(r sin θ)
Comparing real and imaginary parts on both sides
r cos θ = - 1 and r sin θ = 1
Squaring and adding,
r² (cos² θ + sin² θ) = 1 + 1
or r² = 2
∴ r = √2

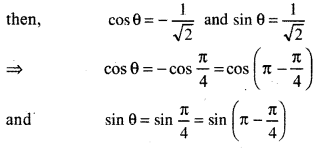
We see that value of cos θ is - ve ⇒ θ will lie in 2^nd or 3^rd quadrant and value of sin θ + ve ⇒ θ will lie in 1^st or 2^nd quadrant ⇒ θ will lie in 2^nd quadrant and graphical representation of complex number - 1 + i will be in 2^nd quadrant.
Thus, θ = \(\frac{3 \pi}{4}\) (∵\(\frac{3 \pi}{4}\) = 135°)
sin 135° = \(\frac{1}{\sqrt{2}}\)
cos 135° = - \(\frac{1}{\sqrt{2}}\)
Then polar form of given expression will be √2 \(\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)\).

(ii) \(\frac{1+3 i}{1-2 i}\)
Answer:

Which will be represented in 2^nd quadrant. Since in 2^nd quadrant X-axis is +ve and Y axis -ve.
Then given expression \(\frac{1+3 i}{1-2 i}\) = - 1 + i
Let - 1 + i = r(cos θ + i sin θ)
⇒ - 1 + i = r cos θ + i(r sin θ)
Comparing real and imaginary parts on both sides
r cos θ = - 1 and r sin θ = 1
Squaring and adding,
r² cos² θ + r² sin² θ = 1 + 1
or r² (cos² θ + sin² θ) = 2
or r² = 2 (∵ cos² θ + sin² θ = 1)
∴ r = √2

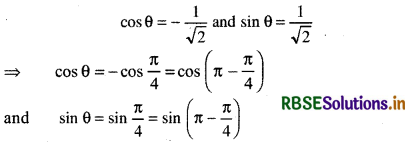
We see that value of cos θ is - ve then θ will lie in 2^nd or 3^rd quadrant and value of sin θ +ve then θ will lie in 1^st or 2^nd quadrant, z will lie in 2^nd quadrant.

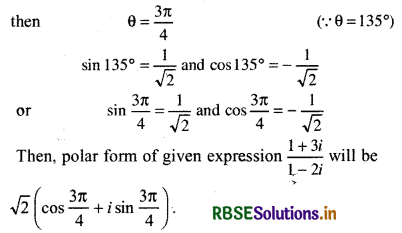
Solve each of the equation in exercise 6 to 9.

Question 6.
3x² - 4x + \(\frac{20}{3}\) = 0
Answer:
Given equation: 3x² - 4x + \(\frac{20}{3}\) = 0
or \(\frac{9 x^2-12 x+20}{3}\) = 0
or 9x² - 12x + 20 = 0 .......... (1)
Comparing with ax² + bx + c = 0
a = 9, b = - 12, c = 20
then discriminant D = b² - 4ac
= (- 12)² - 4 × 9 × 20
= 144 - 720
D = - 576 < 0. i.e.. negative
Thus, solution of equation

Question 7.
x² - 2x + \(\frac{3}{2}\) = 0
Answer:
Given equation: x² - 2x + \(\frac{3}{2}\) = 0
or 2x² - 4x + 3 = 0 ............. (i)
Comparing given equation by ax² + bx + c = 0
a = 2, b = - 4, c = 3
Discriminant of equation is D = b² - 4ac
or D = (- 4)² - 4 × 2 × 3
= 16 - 24
D = - 8 < 0 (Negative)
Now solution of equation

Thus, solutions of given equation (Taking +ve and -ve values separately) are
x = 1 + \(\frac{1}{\sqrt{2}}\)i, 1 - \(\frac{1}{\sqrt{2}}\)i

Question 8.
27x² - 10x + 10
Answer:
Comparing 27x2 - 10x + 1 = 0, with
ax² + bx + c = 0
a = 27, b = - 10, c = 1
Then, discriminant of equation
D = b² - 4ac
= (- 10)² 4 × 27 × 1
= 100 - 108
Thus, solution of equation

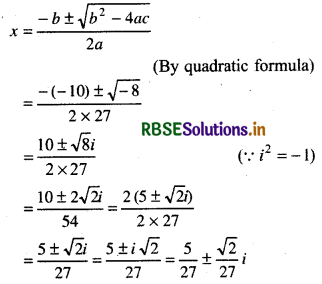
Thus, solutions of given equation (taking +ve and -ve values separately) are
x = \(\frac{5}{27}+\frac{\sqrt{2}}{27}\) i, \(\frac{5}{27}-\frac{\sqrt{2}}{27}\) i

Question 9.
21x² - 28x + 10 = 0
Answer:
Comparing with 21x² - 28x + 10 = 0
ax² + bx + c = 0
a = 21, b = - 28, c = 10
Then, discriminant of equation
D = b² - 4ac
= (- 28)² - 4 × 21 × 10
= 784 - 840
= - 56 = 56i² < 0 [∵ i² = - 1]
Thus, solution of equation

Thus, solutions of given equation (taking +ve and -ve values separately) are
x = \(\frac{2}{3}+\frac{\sqrt{14}}{21}\) i, \(\frac{2}{3}-\frac{\sqrt{14}}{21}\) i

Question 10.
If z₁ = 2 - i, z₂ = 1 + i, find \(\left|\frac{z_1+z_2+1}{z_1-z_2+1}\right|\).
Answer:
z₁ + z₂ + 1 = 2 - i + 1 + i + 1 = 4
z₁ - z₂ + i = 2 - i - (1 + i) + i
z₁ - z₂ + 1 = 2 - 2i
So, therefore

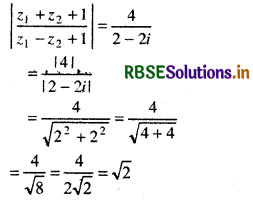
Question 11.
If a + ib = \(\frac{(x+i)^2}{\left(2 x^2+1\right)}\) prove that:
a² + b² = \(\frac{\left(x^2+1\right)^2}{\left(2 x^2+1\right)^2}\)
Answer:
Given,

Second Method:

Question 12.
Let z₁ = 2 - i, z₂ = - 2 + i, find:
(i) Re\(\left(\frac{z_1 z_2}{\bar{z}_1}\right)\)
Answer:
z₁ = 2 - i and z₂ = - 2 + i
Thus, z̄₁ = 2 + i

(ii) Im\(\left(\frac{1}{z_1 \bar{z}_1}\right)\)

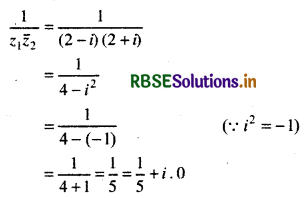
Thus, imaginary part of \(\frac{1}{z_1 \bar{z}_1}\), I_m\(\left(\frac{1}{z_1 \bar{z}_1}\right)\) = 0

Question 13.
Find the modulus and argument of complex number \(\frac{1+2 i}{1-3 i}\).
Answer:

Question 14.
Find the real numbers x and y. If (x - iy) (3 + 5i) is the conjugate of - 6 - 24i.
Answer:
Given, (x - iy) (3 + 5i) is conjugate of complex number - 6 - 24i
∴ (x - iy) (3 + 5i) = - 6 + 24i
[Since conjugate of - 6 - 24i is - 6 + 24i]
or 3x - 3yi + 5ix - 5yi² = - 6 + 24i
or (3x + 5y) + (5x - 3y)i = - 6 + 24i
Comparing real and imaginary parts on both sides
3x + 5y = - 6 ............ (1)
5x - 3y = 24 .............. (2)
Multiply equation (1) by 3 and (2) by 5 and adding
9x + 15y = - 18
25x - 15y = 120
34x = 102
or x = \(\frac{102}{34}\)
34
∴ x = 3
Putting value of x in equation (i)
3 × 3 + 5y = -6
or 9 + 5y = - 6
or 5y = - 6 - 9
or 5y = - 15
∴ y = - 3
Thus, real numbers are x = 3, y = - 3

Question 15.
Find the modulus of \(\frac{1+i}{1-i}\)-\(\frac{1-i}{1+i}\).
Answer:

Question 16.
If (x + iy)³ = u + iv, then show that
\(\frac{u}{x}+\frac{v}{y}\) = 4(x² - y²)
Answer:
Given (x + iy)³ = u + iv
Thus, x³ + i³y³ + 3x .iy(x + iy) = u + iv
[∵ (a + b)³ = a³ + b³ + 3ab(a + b)]
or x³ + i²iy³ + 3x²yi + 3xy² i² = u + iv (∵ i² = - 1)
or x³ - iy³ + 3x²yi - 3xy² = u + iv
or (x³ - 3xy²) + (3x²y - y³)i = u + iv
Comparing real and imaginary parts on both sides
x³ - 3xy² = u and 3x²y - y³ = v
or x(x² - 3y²) = u and y(3x² - y²) = v
or (x² - 3y²) = \(\frac{u}{x}\) and (3x² - y²) = \(\frac{v}{y}\)
Adding, \(\frac{u}{x}+\frac{v}{y}\) = x² - 3y² + 3x² - y²
= 4x² - 4y² = 4(x² - y²)
Thus, \(\frac{u}{x}+\frac{v}{y}\) = 4(x² - y²)
Hence Proved.

Question 17.
If α and β are different complex numbers with |β| = 1, then find \(\left|\frac{\beta-\alpha}{1-\bar{\alpha} \beta}\right|\).
Answer:

Question 18.
Find the number of non-zero integer solutions of the equation |1 - i|^x = 2^x
Answer:
Given |1 - i|^x = 2^x
Now, |1 - i| = \(\sqrt{1^2+(-1)^2}\) = √2 = 2^1/2
Thus, given equation
|1 - i|^x = 2^x
2^x/2 = 2^x
Comparing power on both sides

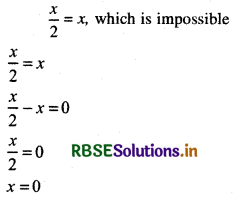
Root is = 0
So, therefore there is no non-zero integral value of x.

Question 19.
If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that:
(a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B²
Answer:
Since,
(a + ib) (c + id) (e + if) (g + ih) = A + iB
So, |(a + ib) (c + id) (e + if) (g + ih)| = |A + iB|
Since, |z₁ z₂| = |z₁| |z₂|
∴ |(a + ib)| |(c + id)| |(e + if)| |(g + ih)| = |A + iB|
or \(\sqrt{\left(a^2+b^2\right)} \sqrt{\left(c^2+d^2\right)} \sqrt{e^2+f^2} \sqrt{g^2+h^2}\) = \(\sqrt{A^2+B^2}\)
Hence Proved.

Question 20.
If \(\left(\frac{1+i}{1-i}\right)^m\) = 1, then find the least positive integral value of m.
Answer:

⇒ i^m = 1 or i^m = (i)^4k
It is possible only when m = 4k,
where m is a positive integer
Since, i² = - 1
i⁴ = (i²)² = (- 1)² = 1
thus, minimum integer value = 4 × 1 = 4