RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2

Find the modulus and the arguments of each of the complex numbers in exercIse 1 and 2.

Question 1.
z = - 1 - i√3
Answer:
First Method: Now, comparing, it with
x cos θ + i sin θ
- 1 = r cos θ and -√3 = r sin θ
Squaring and adding,
1 + 3 = r² cos² θ + r² sin² θ
or 4 = r² (cos² θ + sin² θ)
or r² = 4 (∵ sin² θ + cos² = 1)
or r = 2
Thus r cos θ = - 1 and r sin θ = - √3
cos θ = - \(\frac{1}{2}\) and sin θ = - \(\frac{\sqrt{3}}{2}\)
Thus, line of rotation of angle θ will be in third quadrant.
θ = \(\frac{-2 \pi}{3}\) or \(\frac{4 \pi}{3}\)
Thus, modulus = 2 and argument = - \(\frac{2 \pi}{3}\) or \(\frac{4 \pi}{3}\)

Second Method : Given, z = - 1 - i√3
Comparing with x + ¡y
x = - 1 and y = - √3
∴ Modulus r = \(\sqrt{x^2+y^2}\) (using formula)
r = 4\(\sqrt{(-1)^2+(-\sqrt{3})^2}\)
r = \(\sqrt{1+3}\) = √4 = 2
And argument of given complex number

Question 2.
Z = - √3 + i
Answer:
First Method: On comparing z = - √3 + i with r (cos θ + i sin θ)
- √3 = r cos θ and 1 = r sin θ
Squaring and adding,
r² cos²θ + r² sin² θ = 3 + 1
r² (cos² + sin² θ) = 4
or r² = 4
or r = 2
∴ r cos θ = - √3
and r sin θ = 1
cos θ = - \(\frac{\sqrt{3}}{2}\) and sin θ = \(\frac{1}{2}\)
Then, line of rotation of angle θ will lie in second quadrant.

Second Method:
Given, z = - √3 + i
Comparing with x + iy,
x = - √3 (real part) and y = 1 (imaginary part)
Thus, modulus r = \(\sqrt{x^2+y^2}\) (Using formula)

Convert each of the complex numbers given in exercise 3 to 8 in the polar form.

Question 3.
1 - i
Answer:
Let, z = 1 - i = r(cos θ + i sin θ)
On comparing,
r cos θ = 1 and r sin θ = - 1
Squaring and adding.
r² cos² θ + r² sin² θ = 1 + 1
or r²(cos² θ + sin² θ) = 2
or r² = 2
∴ r = √2

Question 4.
- 1 + i
Answer:
Let, z = - 1 + i = r (cos θ + i sin θ)
Comparing with x + iy
Real part x = - 1, Imaginary part y = 1

Question 5.
- 1 - i
Answer:
Let z = - 1 - i = (r cos θ + ir sin θ)
On comparing
r cos θ = - 1, and r sin θ = - 1
Squaring and adding,
or r² cos² θ + r² sin² θ = 1 + 1
or r² (cos² θ + sin² θ) = 2
or r² = 2 (∵ sin² θ + cos² θ = 1)
then cos θ = - \(\frac{1}{\sqrt{2}}\) and sin θ = - \(\frac{1}{\sqrt{2}}\)
For cos θ = - \(\frac{1}{\sqrt{2}}\), rotation line of θ will lie in second or third quadrant.
and for sin θ = - \(\frac{1}{\sqrt{2}}\), rotation line of θ will lie in third quadrant,
Thus we conclude that rotation line of θ will lie in third quadrant.

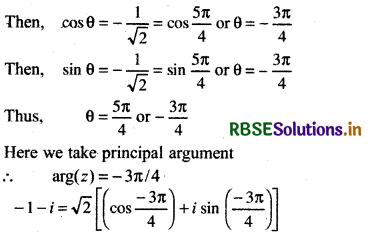
This is the required polar form of given complex number.

Question 6.
- 3
Answer:
Let z = - 3 = r(cos θ + i sin θ)
or z = - 3 + iθ = r(cos θ + i sin θ)
On comparing,
r cos θ = - 3 and r sin θ = 0,
Squaring and adding.
r² cos² θ + r² sin² θ = 9 + 0
or r² (cos² θ + sin² θ) = 9
or r² = 9
or r = 3
⇒ r cos θ = - 3 and r sin θ = 0
Thus, cos θ = \(\frac{-3}{3}\) = - 1 and sin θ = 0
⇒ cos θ = - cos 0° .
and sin θ = sin 0° = sin(π - 0)
then θ = π and θ = π or 2π
it concludes, θ = π
Thus, - 3 = 3 (cos π + i sin π) which is in polar form. since rotation line of given complex number will lie on second quadrant.

Question 7.
√3 + i
Answer:
Let z = √3 + i = r(cos θ + i sin θ)
On comparing,
r cos θ = √3 and r sin θ = 1
Squaring and adding,
r² cos² θ + r² sin² θ = 3 + 1
or r²(cos² θ - r² sin² θ) = 4
or r² = 4
or r = 2.
⇒ From r cos θ = √3 and r sin θ = 1
Thus, cos θ = \(\frac{\sqrt{3}}{2}\) and sin θ = \(\frac{1}{2}\)

Question 8.
i
Answer:
Let z = 0 + i = r(cos θ + i sin θ)
On comparing
r cos θ = 0 or r sin θ = 1
Squaring and adding,
r² cos² θ + r² sin² θ = I
or r² (cos² θ + sin² θ) = I
or r² = 1
or r = 1
⇒ From r cos θ = 0 and r sin θ = I

This is required polar form of given complex answer.