RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1

Express each of the complex number given in the exercise 1 to 10 in the form a + ib:

Question 1.
(5i) (- \(\frac{3}{5}\)i)
Answer:
(5i) \(\left(-\frac{3}{5} i\right)\) = 5 × \(\left(-\frac{3}{5}\right)\) (i²)
= (- 3) (- 1)
= 3
Thus = 3 + 0i

Question 2.
i⁹ + i¹⁹
Answer:
i⁹ + i¹⁹ = (i²)⁴ i + (i²)⁹ i
= (- 1)⁴ i + (- 1)⁹ i (∵ i² = - 1)
= i - 1 × i
= i - i = 0
= 0 + i0

Question 3.
i^-39
Answer:

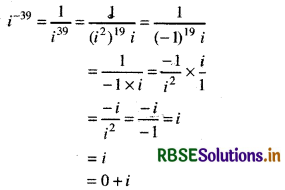
Question 4.
3(7 + i7) + i (7 + i7)
Answer:
3 (7 + i7) + i (7 + i7)
= 21 + 21i + 7i + i² × 7
= 21 + 21i + 7i - 7
= 21 + 28i - 7
= 14 + 28i

Question 5.
(1 - i) - (- 1 + i6)
Answer:
(1 - i) - (- 1 + i6)
= 1 - i + 1 - i6 .
= (1 + 1) - i - i6
= 2 - 7i

Question 6.
\(\left(\frac{1}{5}+i \frac{2}{5}\right)-\left(4+i \frac{5}{2}\right)\)
Answer:

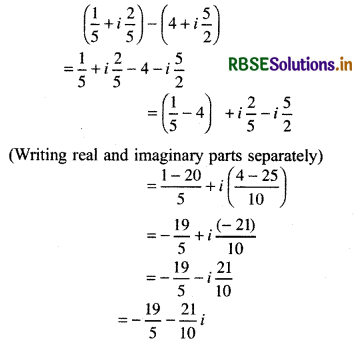
Question 7.
\(\left[\left(\frac{1}{3}+i \frac{7}{3}\right)+\left(4+i \frac{1}{3}\right)\right]-\left(-\frac{4}{3}+i\right)\)
Answer:

Question 8.
(1 - i)⁴
Answer:
(1 - i)⁴ = (1 - i)² (1 - i)²
= (1 + i² - 2i) (1 + i² - 2i)
= (1 - 1 - 2i) (1 - 1 - 2i) (∵ i² = - 1)
= (- 2i) (- 2i) - 4i²
= 4(- 1) = - 4
= - 4 + i0
Thus, (1 - i)⁴ = - 4 + 0i

Question 9.
(\(\frac{1}{3}\) + 3i)³
Answer:

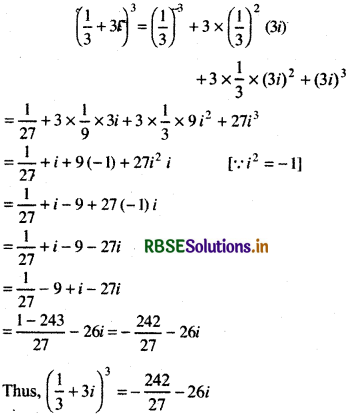
Question 10.
(- 2 - \(\frac{1}{3}\)i)³
Answer:

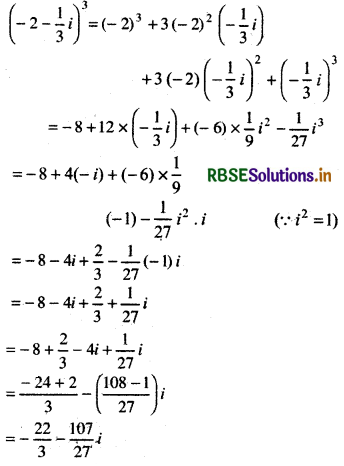
Find the multiplicative inverse of each of the complex numbers given in the exercise 11 to 13.

Question 11.
4 - 3i
Solution:
Let = 4 - 3i
then, z̄ = \(\overline{4-3 i}\) = 4 + 3i
∴ |z| = \(\sqrt{(4)^2+(-3)^2}\)
and |z|² = (4)² + (3)²
or |z|² = 16 + 9 or |z|² = 25
Multiplicative Inverse of z = 4 - 3i
z^-1 = \(\frac{\bar{z}}{|z|^2}=\frac{4+3 i}{25}=\frac{4}{25}+\frac{3}{25}i\)
Thus, multiplicative inverse of = \(\frac{4}{25}+\frac{3}{25}i\)

Second Method:
z^-1 = \(\frac{1}{4-3 i}\) = \(\frac{(4+3 i)}{(4-3 i)(4+3 i)}\)
Multiplying conjugate of denominator in numerator and denominator

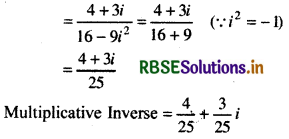
Question 12.
√5 + 3i
Answer:
Let z = √5 + 3i
then, z̄ = \(\overline{\sqrt{5}+3 i}\) = √5 - 3i
and |z|² = (√5)² = (3)²
= 5 + 9 = 14
Thus, multiplicative inverse of z = √5 + 3i

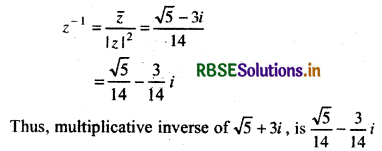
Second Method:

Question 13.
- i
Answer:
Let z = - i = 0 - i
conjugate z̄ = -\(\overline{0-i}\) = 0 + i
∴ |z| = \(\sqrt{(0)^2+(-1)^2}\)
|z|² = (- 1)² = 1
Now, z^-1 = \(\frac{\bar{z}}{|z|^2}=\frac{i}{1}\)
= \(\frac{i}{1}\) = i
or z^-1 = i
Thus, multiplicative inverse of z = - i is i.

Second Method:
z = - i

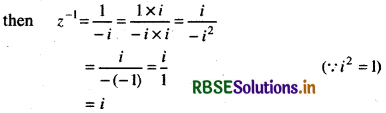
Thus, multiplicative inverse of z = - i will be i.

Question 14.
Express the following expression in the form of a + ib.
\(\frac{(3+i \sqrt{5})(3-i \sqrt{5})}{(\sqrt{3}+\sqrt{2} i)-(\sqrt{3}-i \sqrt{2})}\)
Answer: