RBSE Solutions for Class 11 Maths Chapter 4 गणितीय आगमन का सिद्धांत Ex 4.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 4 गणितीय आगमन का सिद्धांत Ex 4.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 4 गणितीय आगमन का सिद्धांत Ex 4.1

सभी n ∈ N के लिए गणितीय आगमन सिद्धान्त के प्रयोग द्वारा सिद्ध कीजिए कि:

प्रश्न 1.
1 + 3 + 3² + ......... + 3^n-1 = \(\frac{\left(3^n-1\right)}{2}\)
हल:
माना
P(n) : 1 + 3 + 3² + ......... + 3^n-1 = \(\frac{\left(3^n-1\right)}{2}\)
सिद्ध करना है P (1) सत्य है ।
n = 1 के लिए
R.H.S. = \(\frac{3^1-1}{2}=\frac{2}{2}\) = 1 = T₁ = L.H.S
∴ L.H.S. = R.H.S.
अत: P (1) सत्य है ।
माना कि P (k) भी सत्य होगा
1 + 3 + 3² + ......... + 3^k-1 = \(\frac{\left(3^k-1\right)}{2}\) .....(1)
सिद्ध करना है P(k + 1) सत्य है अर्थात्
1 + 3 + 3² + ......... + 3^n-1 + 3^k = \(\frac{3^{k+1}-1}{2}\)
L.H.S.= 1 + 3 + 3² + .............. + 3^k-1 + 3^k
= (1 + 3 + 32 + ......... + 3^k-1) + 3^k
= \(\frac{3^k-1}{2}\) + 3^k
[समीकरण (1) से मान रखने पर ]
= \(\frac{3^k-1+2.3^k}{2}=\frac{3^k(1+2)-1}{2}=\frac{3.3^k-1}{2}\)
= \(\frac{3^{k+1}-1}{2}\) = R.H.S
अत: P(k + 1) सत्य है । जब कभी P (k) सत्य है. अतः गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P (n) सत्य है।

प्रश्न 2.
1³ + 2³ + 3³ + ........... + n³ = \(\left(\frac{n(n+1)}{2}\right)^2\)
हल:
माना कि
P(n) = 1³ + 2³ + 3³ + ........... + n³ = \(\left(\frac{n(n+1)}{2}\right)^2\)
सिद्ध करना है – P(1) सत्य है ।
n = 1 के लिए
R.H.S. = \(\left[\frac{n(n+1)}{2}\right]^2\)
= \(\left[\frac{n(n+1)}{2}\right]^2\) = (1)² = 1 = 1³ = T₁ = L.H.S.

अर्थात् P(1) सत्य है ।
माना कि P(k) भी सत्य है ।
1³ + 2³ + 3³ + ........... + k³ = \(\left[\frac{k(k+1)}{2}\right]^2\) ...........(1)
सिद्ध करना है — P(k + 1) सत्य है ।
या 1³ + 2³ + 3³ + ........... + k³ + (k + 1)³ = \(\left[\frac{(k+1)(k+2)}{2}\right]^2\)

अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है ।
अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P (n) सत्य है ।

प्रश्न 3.
1 + \(\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+\ldots \ldots .+\frac{1}{(1+2+3+\ldots . . n)} = \frac{2 n}{(n+1)}\)
हल:
माना कि
P(n) = 1 + \(\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+\ldots \ldots .+\frac{1}{(1+2+3+\ldots . . n)} = \frac{2 n}{(n+1)}\)
सिद्ध करना है – P (1) सत्य है ।
n = 1 के लिए
R.H.S. = \(\frac{2 n}{n+1}=\frac{2.1}{1+1}=\frac{2}{2}\) = 1 = T₁ = L.H.S.
अत: L.H.S. = R.H.S.
अत: P (1) सत्य है ।
माना कि P(k) सत्य है ।

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है । जब कभी P( k ) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 4.
1.2.3 + 2.3.4 + ...................... + n (n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
हल:
माना कि
P (n) : 1.2.3 + 2.3.4 + ...................... + n (n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
सिद्ध करना है - P (1) सत्य है ।

अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है। अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 5.
1.3 + 2.3² + 3.3³ + ........... +n.3ⁿ = \(\frac{(2 n-1) 3^{n+1}+3}{4}\)
हल:
माना कि P (n) : 1.3 + 2.3² + 3.3³ + ........... +n.3ⁿ = \(\frac{(2 n-1) 3^{n+1}+3}{4}\)
सिद्ध करना है – P (1) सत्य है । ∴ n = 1 के लिए

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अतः गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 6.
1.2 + 2.3 + 3.4 + .............. + n(n + 1) = \(\left[\frac{n(n+1)(n+2)}{3}\right]\)
हल:
माना कि P (n) : 1.2 + 2.3 + 3.4 + .............. + n(n + 1) = \(\left[\frac{n(n+1)(n+2)}{3}\right]\)
सिद्ध करना है - P (1) सत्य है । ∴ n = 1 के लिए

अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 7.
1.3 + 3.5 + 5.7 + ...... + (2n - 1)(2n + 1) = \(\frac{n\left(4 n^2+6 n-1\right)}{3}\)
हल:
माना कि P(n) : 1.3 + 3.5 + 5.7 + ...... + (2n - 1)(2n + 1) = \(\frac{n\left(4 n^2+6 n-1\right)}{3}\)
सिद्ध करना है कि P( 1 ) सत्य है । अत: n = 1 के लिए
R.H.S = \(\frac{n\left(4 n^2+6 n-1\right)}{3}=\frac{1\left(4 \times 1^2+6 \times 1-1\right)}{3}\)
= \(\frac{4+6-1}{3}\) = 3 = 1.3 = T₁
L.H.S. = R.H.S.
अत: P (1) सत्य है ।
माना कि P (k) सत्य होगा ।
अत: 1.3 + 3.5 + 5.7 + ................ + (2k - 1) (2k + 1) = \(\frac{k\left(4 k^2+6 k-1\right)}{3}\) .........(1)

सिद्ध करना है कि P(k + 1) सत्य है। इसके लिए
1.3 + 3.5+ 5.7 + ............ + (2k - 1) (2k + 1)

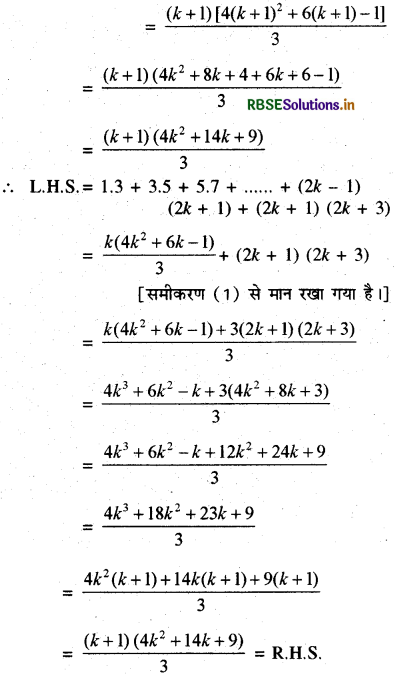
L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P (n) सत्य है ।

प्रश्न 8.
1.2 + 2.2² + 3.2³ + .......... + n.2ⁿ = (n - 1)2ⁿ⁺¹ + 2
हल:
माना कि P (n) : 1.2 + 2.2² + 3.2³ + .............. + n.2ⁿ = (n - 1) 2ⁿ⁺¹ + 2
सिद्ध करना है कि P (1) सत्य है । अत: n = 1 के लिए
R.H.S = (n - 1)2ⁿ⁺¹ + 2
= (1 - 1)2¹⁺¹ + 2 = 2 = 1.2 = T₁ = L.H.S.
अत: P(1) सत्य है ।
माना कि P (k) सत्य है ।
अंतः 1.2 + 2.2² + 3.2³ + ................ + k.2k = (k – 1)
2k + 1 + 2 .....(1)
सिद्ध करना है कि P(k + 1) सत्य है । इसके लिए
1.2 + 2.2² + 3.2³ + + k.2^k + (k + 1)2^k+1 = k.2^k+2 + 2
L.H.S. = 1.2 + 2.2² + 3.2³ + + k.2^k + (k + 1)2^k+1
= [(k - 1)2^k+1 + 2] + (k + 1)2^k+1 + 2
[समीकरण (1) से मान रखा गया है । ]
L.H.S. = (k + 1 + k - 1)2^k+1 + 2
= 2k.2^k+1 + 2 = k. 2^k+2 + 2 = R.H.S.
L.H.S = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P (k + 1) सत्य है जब कभी P (k) सत्य है । अतः गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है।

प्रश्न 9.
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots \ldots+\frac{1}{2^n}=1-\frac{1}{2^n}\)
हल:
माना कि P(n) : \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots \ldots+\frac{1}{2^n}=1-\frac{1}{2^n}\)
सिद्ध करना है कि P(1) सत्य है । अत: n = 1 के लिए
R.H.S. = 1 - \(\frac{1}{2^n}\) = 1 - \(\frac{1}{2^1}=\frac{1}{2}\)
L.H.S. = R.H.S.
अत: P(1) सत्य है।
माना कि P(k) भी सत्य होगा ।

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 10.
\(\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+\ldots \ldots+\frac{1}{(3 n-1)(3 n+2)} = \frac{n}{(6 n+4)}\)
हल:
माना कि P (n) : \(\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+\ldots \ldots+\frac{1}{(3 n-1)(3 n+2)} = \frac{n}{(6 n+4)}\)
सिद्ध करना है कि P( 1 ) सत्य है । ∴ n = 1 के लिए
R.H.S. = \(\frac{n}{6 n+4}=\frac{1}{6 \times 1+4}=\frac{1}{10}=\frac{1}{2.5}\) = T₁ = L.H.S
L.H.S. = R.H.S.
अत: P (1) सत्य है ।
माना कि P (k) सत्य होगा ।

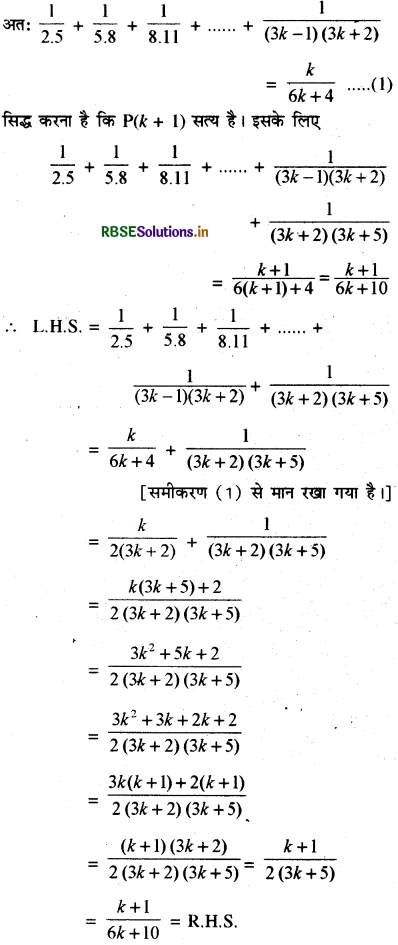
L.H.S = R.H.S
अत: P(k + 1) सत्य है ।
इस प्रकार P ( k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन.P(n) सत्य है।

प्रश्न 11.
\(\frac{1}{1.2 .3}+\frac{1}{2.3 .4}+\frac{1}{3.4 .5}+\ldots \ldots+\frac{1}{n(n+1)(n+2)} = \frac{n(n+3)}{4(n+1)(n+2)}\)
हल:
माना कि P (n) :\(\frac{1}{1.2 .3}+\frac{1}{2.3 .4}+\frac{1}{3.4 .5}+\ldots \ldots+\frac{1}{n(n+1)(n+2)} = \frac{n(n+3)}{4(n+1)(n+2)}\)
सिद्ध करना है कि P (1) सत्य है । ∴ n = 1 के लिए
R.H.S = \(\frac{n(n+3)}{4(n+1)(n+2)}=\frac{1(1+3)}{4(1+1)(1+2)}=\frac{1 \times 4}{4 \times 2.3}=\frac{1}{1.2 .3}\) = T₁
L.H.S. = R.H.S.
अत: P(1) सत्य है ।
माना कि P(k) भी सत्य होगा ।

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 12.
a + ar + ar² + ............... + ar^n-1 = \(\frac{a\left(r^n-1\right)}{r-1}\)
हल:
माना कि P (n): a + ar + ar² + ............... + ar^n-1 = \(\frac{a\left(r^n-1\right)}{r-1}\)
सिद्ध करना है कि P (1) भी सत्य है । ∴ n = 1 के लिए
R.H.S. = \(\frac{a\left(r^n-1\right)}{r-1}=\frac{a(r-1)}{r-1}\) = a = T₁
L.H.S. = R.H.S.
अत: P(1) सत्य है।
माना कि P(k) भी सत्य होगा ।
अत: a + ar + ar² + ............... + ar^k-1 = \(\frac{a\left(r^k-1\right)}{r-1}\)
सिद्ध करना है कि P( k + 1) सत्य है । या
a + ar + ar² + ...... + ar^k-1 + ar^k = \(\frac{a\left(r^{k+1}-1\right)}{r-1}\)
L.H.S. = (a + ar + ar² + ...... + ar^k-1) + ar^k

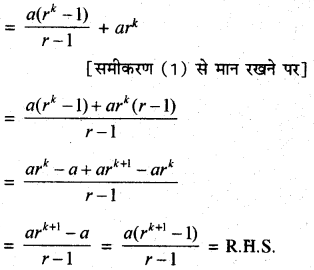
L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P (k + 1) सत्य है जब कभी P ( k ) सत्य है । अतः गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 13.
(1 + \(\frac{3}{1}\))(1 + \(\frac{5}{4}\))(1 + \(\frac{7}{9}\)) ........... (1 + \(\frac{(2 n+1)}{n^2}\)) = (n + 1)²
हल:
माना कि P (n) : (1 + \(\frac{3}{1}\))(1 + \(\frac{5}{4}\))(1 + \(\frac{7}{9}\)) ........... (1 + \(\frac{(2 n+1)}{n^2}\)) = (n + 1)²
सिद्ध करना है कि P(1) सत्य है । अत: n = 1 के लिए
R.H.S. = (n + 1)² = (1 + 1)² = 4 = (1 + \(\frac{3}{1}\)) = T₁
L.H.S. = R.H.S.
अत: P(1) सत्य है ।
माना कि P ( k ) भी सत्य है ।

L.H.S.= R.H.S.
अत: P(k + 1) सत्य है
इस प्रकार P ( k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 14.
(1 + \(\frac{1}{1}\))(1 + \(\frac{1}{2}\))(1 + \(\frac{1}{3}\)) ............... (1 + \(\frac{1}{n}\)) = (n + 1)
हल:
माना कि P (n) : (1 + \(\frac{1}{1}\))(1 + \(\frac{1}{2}\))(1 + \(\frac{1}{3}\)) ............... (1 + \(\frac{1}{n}\)) = (n + 1)
सिद्ध करना है कि P (1) सत्य है । ∴ n = 1 के लिए
R.H.S. = (n + 1) = (1 + 1) = (1 + \(\frac{1}{1}\)) = T₁
L.H.S. = R.H.S.
अत: P(1) सत्य है ।
माना कि P (k) भी सत्य होगा ।

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अतः गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 15.
1² + 3² + 5² + ....... + (2n - 1)² = \(\frac{n(2 n-1)(2 n+1)}{3}\)
हल:
माना कि P(n) : 1² + 3² + 5² + ....... + (2n - 1)² = \(\frac{n(2 n-1)(2 n+1)}{3}\)
सिद्ध करना है कि P (1) सत्य है । ∴ n = 1 के लिए
R.H.S. = \(\frac{n(2 n-1)(2 n+1)}{3}\)
= \(\frac{1(2 \times 1-1)(2 \times 1+1)}{3}=\frac{1 \times 1 \times 3}{3}\) = 1 = 1² = T₁
L.H.S. = R.H.S.
अत: P (1) सत्य है ।
माना कि P (k) भी सत्य होगा ।

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 16.
\(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+\ldots \ldots+\frac{1}{(3 n-2)(3 n+1)}=\frac{n}{(3 n+1)}\)
हल:
माना कि P (n) : \(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+\ldots \ldots+\frac{1}{(3 n-2)(3 n+1)}=\frac{n}{(3 n+1)}\)
सिद्ध करना है कि P (1) सत्य है । अत: n = 1 के लिए
R.H.S. = \(\frac{n}{3 n+1}=\frac{1}{3 \times 1+1}=\frac{1}{4}=\frac{1}{1.4}\) = T₁
L.H.S.= R.H.S.
अत: P(1) सत्य है।
माना कि P ( k ) भी सत्य होगा ।

अतः L.H.S. = R.H.S.
अत: P(k + 1) सत्य है।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P (n) सत्य है ।

प्रश्न 17.
\(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \ldots \ldots+\frac{1}{(2 n+1)(2 n+3)}=\frac{n}{3(2 n+3)}\)
हल:
माना कि P(n) : \(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots \ldots \ldots+\frac{1}{(2 n+1)(2 n+3)}=\frac{n}{3(2 n+3)}\)
सिद्ध करना है कि P (1) सत्य है । अत: n = 1 के लिए
R.H.S. = \(\frac{n}{3(2 n+3)}=\frac{1}{3(2 \times 1+3)}=\frac{1}{3.5}\) = T₁
L.H.S. = R.H.S.
अत: P(1) सत्य है।
माना कि P (k) भी सत्य होगा ।

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 18.
1 + 2 + 3 + ............. + n < \(\frac{1}{8}\)(2n + 1)²
हल:
माना कि P(n) : 1 + 2 + 3 + ...... + n < \(\frac{1}{8}\)(2n + 1)²
सिद्ध करना है कि P (1) सत्य है । ∴ n = 1 के लिए
1 < \(\frac{1}{8}\)(2 × 1 + 1)²
या 1 < \(\frac{9}{8}\) जो कि सत्य है ।
L.H.S. = R.H.S.
अत: P(1) सत्य है।
माना कि P(k) भी सत्य होगा । अतः
1+ 2+ 3 + .............. + k < \(\frac{1}{8}\) (2k + 1)² .....(1)
सिद्ध करना है कि P (k + 1) सत्य है । इसके लिए

L.H.S. = R.H.S.
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P (n) सत्य है ।

प्रश्न 19.
n(n + 1) (n + 5), संख्या 3 का एक गुणज है ।
हल:
माना P(n) : n (n + 1) (n + 5), संख्या 3 का एक गुणज है ।
सिद्ध करना है कि P (1) सत्य है । अत: n = 1 के लिए
n (n + 1) (n + 5) = 1(1 + 1)(1 + 5) = 12 जो
कि 3 का एक गुणज है ।
अत: P(1) सत्य है।
माना कि P( k ) भी सत्य होगा । अतः
k(k + 1) (k + 5) भी 3 का एक गुणज है I
सिद्ध करना है कि P ( k + 1) सत्य है । या
(k + 1) (k + 2) (k + 6) भी 3 का एक गुणज है
∴ (k + 1) (k + 2) (k + 6)
= (k + 1) (k + 2) ( k + 5 + 1 )
= (k + 1) (k + 2) (k + 5) + 1(k+ 1) (k + 2)
= (k + 1) (k + 2) k + 5(k + 1) (k + 2) + (k + 1) (k + 2)

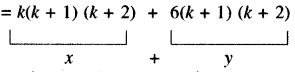
यहाँ x, 3 का गुणज है तथा y भी 3 का गुणज है । अत: x + y भी 3 का गुणज होगा । अत: P (k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 20.
10^2n-1 + 1 संख्या 11 से भाज्य है ।
हल:
माना कि P (n) : 10^2n-1 - 1 + 1 संख्या 11 से भाज्य है ।
सिद्ध करना है कि P( 1 ) सत्य है । अत: n = 1 के लिए
10^2n-1 + 1 = 10^2×1-1 + 1 = 10 + 1 = 11 जो कि 11 से भाज्य है ।
L.H.S. = R.H.S.
अतः P(1) सत्य है।
माना कि P(k) भी सत्य होगा । अर्थात्
10^2k-1 + 1 भी 11 से भाज्य होगी।
सिद्ध करना है कि P (k + 1) सत्य है । अतः
10^2(k+1)-1 + 1 = 10^2k+2-1+ 1
= 10². 10^2k-1 + 1
= 100. 10^2k-1 + 1
= 100(10^2k-1 + 1) - 100 + 1

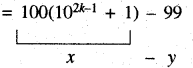
यहाँ x तथा दोनों ही संख्या 11 से भाज्य हैं अतः x - y .11 से भाज्य होगी। अत: P (k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है। अतः गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 21.
x²ⁿ – y²ⁿ, (x + y) से भाज्य है ।
हल:
माना कि P(n) : x²ⁿ – y²ⁿ, (x + y) से भाज्य है ।
सिद्ध करना है कि P (1) सत्य है । अत: n = 1 के लिए
x²ⁿ - y²ⁿ = x^2×1 - y^2×1 = x² - y² जो कि (x + y) से भाज्य है ।
L.H.S. = R.H.S.
अतः P(1) सत्य है ।
माना कि P(k) भी सत्य होगा। अतः
x^2k - y^2k भी x + y से भाज्य है ।
सिद्ध करना है कि P( k + 1) सत्य है। इसके लिए
x^2(k+1) - y^2(k+1), x + y से भाज्य है।
x^2k+2 - y^2k+2, x + y से भाज्य है।
∴ x^2k+2 - y^2k+2
= x^2k.x² - y^2k. y²
= x².x^2k - x²y^2k + x²y^2k - y²y^2k

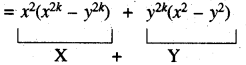
X तथा Y दोनों ही x + y से भाज्य हैं अत: X + Y भी x + y से भाज्य होगा ।
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 22.
3²ⁿ⁺² - 8n - 9, संख्या 8 से भाज्य है ।
हल:
माना कि P(n) : 3²ⁿ⁺⁺² - 8n - 9, संख्या 8 से भाज्य है ।
सिद्ध करना है कि P ( 1 ) सत्य है । अत: n = 1 के लिए
3²ⁿ⁺² - 8n - 9 = 3^2×1+2 - 8 × 1
= 81 - 9 = 64
जो कि 8 से भाज्य है । अत: P(1) सत्य है
माना कि P(k) भी सत्य है । अर्थात्
3^2k+2 - 8k 9, 8 से भाज्य है ।
सिद्ध करना है कि P(k + 1) सत्य है । अर्थात्
3^2(k+1)+2 - 8 (k + 1) - 9, 8 से भाज्य है
3^2k+4 - 8 (k + 1) - 9, 8 से भाज्य है ।
अतः 3^2k+4 - 8 (k + 1)
= 3^2k+2+2 - 8k - 8 - 9
= 3^2k+2 3² - 8k - 8 - 9
= 9(3^2k+2 - 8k - 9) + 72k + 81
= 9 (3^2k+2 - 8k - 9) + 64k - 64

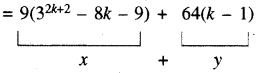
x तथा y में दी गई राशियाँ 8 से भाज्य हैं अतः x + y से प्राप्त राशि भी 8 से भाज्य होगी। अतः x + y 8 से भाज्य है । अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P (k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 23.
41ⁿ - 14ⁿ, संख्या 27 का एक गुणज है ।
हल:
माना कि P (n) : 41ⁿ – 14ⁿ, संख्या 27 का एक गुणज है । सिद्ध करना है कि P (1) सत्य है ।
अत: n = 1 के लिए 41ⁿ - 14ⁿ = 41¹ - 14¹ = 27 जो कि 27 का एक गुणजं है।
अत: P(1) सत्य है माना कि P (k) भी सत्य होगा । अतः
41^k - 14^k, 27 का एक गुणज है
सिद्ध करना है कि P (k + 1) सत्य है । या
41^k+1 - 14^k+1, 27 का एक गुणज है ।
अर्थात् (41)^k+1 - (14)^k+1
= 41(41)^k – 14(14)^k
= 41(41)^k − 41(14)^k + 41(14)^k - 14(14)^k
= 41[(41)^k − (14)^k] + 41(14)^k − 14(14)^k
= 41[(41)^k - (14)^k] + (14)^k [41 - 14]

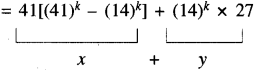
यहाँ x तथा y दोनों ही 27 की गुणज हैं अतः x + y भी 27 की गुणज होगी। अतः x + y, 27 की गुणज है ।
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है ।

प्रश्न 24.
(2n + 7) < (n + 3)²
हल:
माना कि P (n) : (2n + 7) < (n + 3)²
सिद्ध करना है कि P(1) सत्य है । अत: n = 1 के लिए
⇒ (2n + 7) < (n + 3)²
⇒ (2 × 1 + 7) < (1 + 3)²
⇒ 9 < 16 जो कि सत्य है ।
अत: P(1) सत्य है।
माना कि P (k) भी सत्य होगा । अतः
2k + 7 < (k + 3)²
सिद्ध करना है कि P(k + 1) सत्य है । इसके लिए
2(k + 1) + 7 < (k + 1 + 3)²
2k + 9 < (k + 4)²
माना गया है कि 2k + 7 < (k + 3)²
दोनों पक्षों में 2 जोड़ने पर
⇒ 2k + 7 + 2 < (k + 3)² + 2
⇒ 2k + 9 < k² + 9 + 6k + 2
⇒ 2k + 9 < k² + 6k + 11 .... (i)
अब k² + 6k + 11 < k² + 8k + 16 .........(ii)
या k² + 6k + 11 < (k + 4)²
समीकरण (i) व (ii) से
2k + 9 < (k + 4)²
अत: P(k + 1) सत्य है ।
इस प्रकार P(k + 1) सत्य है जब कभी P(k) सत्य है । अत: गणितीय आगमन सिद्धान्त से सभी प्राकृत संख्याओं N के लिए कथन P (n) सत्य है ।