RBSE Solutions for Class 11 Maths Chapter 4 Principle of Mathematical Induction Ex 4.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 4 Principle of Mathematical Induction Ex 4.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 4 Principle of Mathematical Induction Ex 4.1

Prove the following by using the principle of mathematical induction for all n ∈ N.

Question 1.
1 + 3 + 3² + .................... + 3^{n - 1} = \(\left(\frac{3^n-1}{2}\right)\)
Answer:
Let given statement is P(n), i. e.,
P (n): 1 + 3 + 3² + ....... + 3^{n - 1} = \(\left(\frac{3^n-1}{2}\right)\)
When n = 1, P(1): 1 = \(\frac{3^1-1}{2}\) = 1.
Thus, given statement is true for n = 1, i.e., P(1) is true.
Again, Let given statement is true for n = k, i.e.,
P(k): 1 + 3 + 3² + ....... + 3^{k - 1} = \(\left(\frac{3^k-1}{2}\right)\) ............... (1)
Now, we will prove that given statement is true Tor n = k + 1 i.e., P(k + 1) is true. .
Now, P(k + 1) : (1 + 3 + 3² + ..................... + 3^{k - 1}) + 3^k

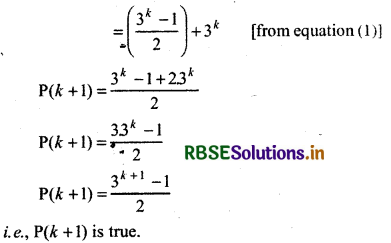
Thus, by principle of mathematical induction statement is true for all natural numbers n i.e., P(n) is true.
Hence Proved.

Question 2.
1³ + 2³ + 3³ + ............... + n³ = \(\left[\frac{n(n+1)}{2}\right]^2\)
Answer:
Let given statement is P(n), here n ∈ N.
Then, P(n):1³ + 2³ + 3³ + ......... + n³

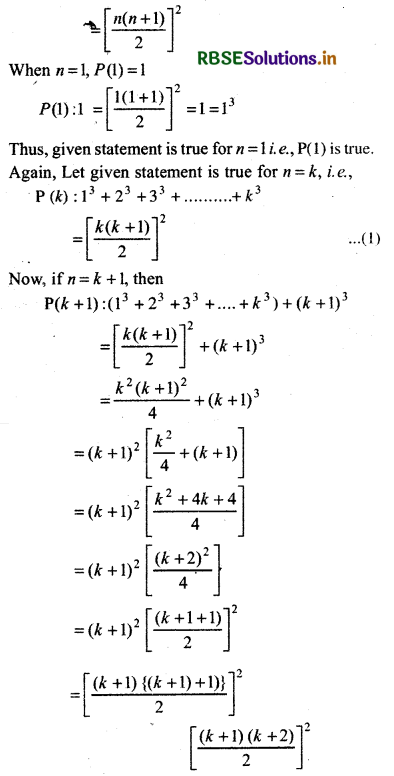
We see that given statement is true for n = k + 1 i.e., P(k + 1) is true.
So we can say that given statement is true for all natural numbers i.e., p(n) is true.
Hence Proved.

Question 3.
\(1+\frac{1}{(1+2)}+\frac{1}{(1+2+3)}+\ldots+\frac{1}{(1+2+3+\ldots+n)}=\frac{2 n}{n+1}\)
Answer:
Let given statement is P(n), where n ∈ N.

We see that given statement is true for n = k + 1 i.e., P(k + 1) is true.
So, we can say that given statement is true for all natural numbers n ∈ N, by principle of-mathematical induction.
Hence Proved

Question 4.
1.2.3 + 2.3.4 + ...... + n(n + 1) (n + 2) = \(\frac{n(n+1)(n+2)(n+3)}{4}\)
Answer:
Let given statement P(n), where n ∈ N i.e.,
P(n): 123 + 23.4 + ........ + n(n + 1) (n + 2)

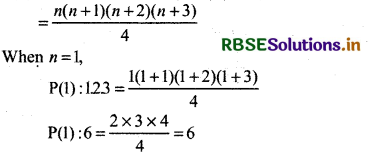
Thus, given statement is true for n -1, i.e., P(1) is true.
Again, Let given statement is true for n = k i.e.,
P(k): 1.23 + 23.4 + ....... + k(k + 1) (k + 2)
= \(\frac{k(k+1)(k+2)(k+3)}{4}\) .............. (1)
Now, we will prove that given statement is true for n = k + 1, i. e, P(k + 1) is true.
Now
P(k + 1): [1.23 + 23.4 + ...... + k(k + 1) (k + 2)] + (k + 1) (k + 2) (k + 3)

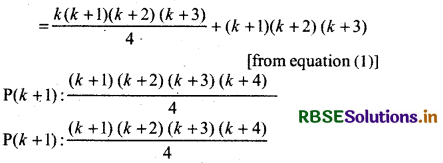
Thus, statement is true for n = k + 1, i.e., P(k + 1) is true.
Therefore, by principle of mathematical induction we can say that given statement is true for all natural numbers n.
Hence Proved

Question 5.
1.3 + 2.3² + 3.3³ +....... + n. 3ⁿ = \(\frac{(2 n-1) 3^{n+1}+3}{4}\)
Answer:
Let given statement is P(n) where n ∈ N.
Then, P(n): 1.3 + 2.3² + 3.3³ + ....... + n³ⁿ (2n-l)3” + 1 +3

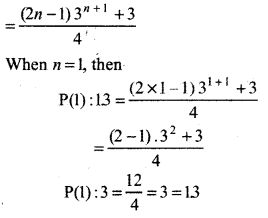
Thus, P(n) is true for n = 1, i.e., P(1) is true.
Again, Let P(n) is true for n = k, i.e.,
P(k): 13 + 2.3² + 3.3³ + ............. + k.3^k
= \(\frac{(2 k-1) 3^{k+1}+3}{4}\) ............... 91)
Now we will prove that P(n) is true for n = k + 1, i, e., P(k + 1) is true.
Now P(k + 1):1.3 + 2.3² + 3.3³ + ...... + k.3^k + (k + 1)3^{k + 1}

Thus, P(n) is true for n = k + 1 i. e., P(k + 1) is true.
Thus, by principle of mathematical induction given statement is true for all n ∈ N.
Hence Proved

Question 6.
1.2 + 2.3 + 3.4 + .............. + n(n + 1) = \(\left[\frac{n(n+1)(n+2)}{3}\right]\).
Answer:
Let given statement is P(n), here n ∈ N i.e,
P(n): 1.2 + 2.3 + 3.4 + ..... + n(n + 1)
= \(\left[\frac{n(n+1)(n+2)}{3}\right]\)
When n = 1, then
P(1) : 12 = 2 = \(\frac{1(1+1)(1+2)}{3}\) = 2 = 12
Thus, given statement is true for n = 1
i.e., P(1) is true.
Let p(n) is true for n = k. Thus,
P(k): 1.2+ 2.3+ 3.4 + ....... + k(k + 1)
= \(\left[\frac{k(k+1)(k+2)}{3}\right]\) ........... (1)
Now we will prove that P(n) is true for n = k + 1 i. e., P(k + 1) is true.
Now P(k + 1): [1.2 + 2.3 + 3.4 + ....... + k(k + 1)] + (k + 1) . (k + 1 + 1)

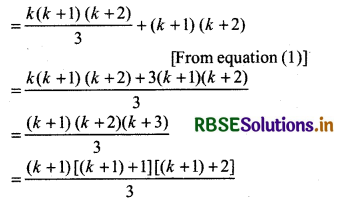
Thus, given statement is true for n = k + 1 i.e., P(k + 1) is also true.
Thus, by principal of mathematical induction we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 7.
1.3 + 3.5 + 5.7 + ........ + (2n - 1) (2n + 1) = \(\frac{n\left(4 n^2+6 n-1\right)}{3}\)
Answer:
Let given statement is P(n) where n ∈ N i.e.,
P(n): 1.3 + 3.5 + 5.7 + ......... + (2n - 1) (2n + 1)
= \(\frac{n\left(4 n^2+6 n-1\right)}{3}\)
where n = 1,
P(1) : 13 = 3 = \(\frac{1 \times\left(4 \times 1^2+6 \times 1-1\right)}{3}\)
= \(\frac{9}{3}\) = 3 = 13
Thus, given statement is true for n = 1 i.e., P(1) is true.
Again, let given statement is true for n = k i.e.,
p(k): 1.3 + 3.5 + 5.7 + ........... + (2k - 1) (2k + 1)
= \(\frac{k\left(4 k^2+6 k-1\right)}{3}\) ............. (1)
Now we will show that given statement is true for n = k + 1, i.e., p(k + 1) is true.
Now
p(k + 1) : [1.3 + 3.5 + 5.7 + ......... + (2k - 1)
[(2k + 1)] {2(k + 1) - 1} {2(k + 1) + 1}

Thus, given statement is true for n = k + 1 i.e., P(k + 1) is true.
Therefore, by principal of mathematical induction we can say that given statement is true for all natural numbers
n ∈ N.
Hence Proved

Question 8.
1.2 + 2.2² + 3.2² + .......... + n.2ⁿ = (n - 1)2^{n + 1} + 2
Answer:
Let given statement is P(n) where n ∈ N.
i.e. P(n): 1.2 + 2.2² + 3.2² + ................. + n.2ⁿ
= (n - 1)2^{n + 1} + 2
Now. if n = 1,
Then, P(1):1² = 2 = (1 - 1)² + 2 = 2
Therefore, given statement is true for n = I i.e., P(1) is
true.
Again, let given statement is true for n = k i.e., P(k) is true.
Thus, P(k) : 1.2 + 2.2² + 3.2² + ....... k.2^k
= (k - 1)2^{k + 1} + 2 ............. (1)
Now, we will show that given statement n = k + 1, i.e., P(k + 1) is also true.
Thus P(k + 1): (1.2 + 2.2² + 3.2³ + .................. + k.2^k) + (k + 1)2^{k + 1}
= (k - 1)2^{k + 1} + 2 + (k + 1)2^{k + 1} [From equation (1)]
= 2^{k + 1} {k - 1 + k + 1} + 2
= 2k.2^{k + 1} + 2 = k.2^{k + 2} + 2
= [(k + 1) - 1)]2^{(k + 1) + 1} + 2
Thus, given statement n = k + 1, i.e., P(k +1) is true.
Then, by principal of mathematical induction, given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 9.
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots+\frac{1}{2^n}=1-\frac{1}{2^n}\)
Answer:
Let given statement is P(n), where n ∈ N,
If n = 1, then
P(1) : \(\frac{1}{2}=1-\frac{1}{2^1}=1-\frac{1}{2}=\frac{1}{2}\)
Thus, given statement n = 1, i.e., true for p(1). Again, let given statement n = k, i.e., P(k) is true i.e.,
P(k): \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots .+\frac{1}{2^k}=1-\frac{1}{2^k}\) .......... (1)
Now, we will show that given statement n = k + 1 i.e.,
P(k + 1) will be true.

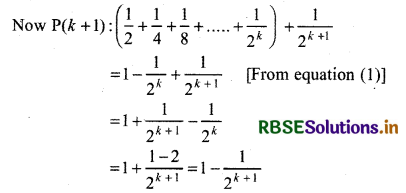
Thus, given statement n = k + 1 i.e., p(k + 1) is also true.
Thus, by principal of mathematical induction we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved

Question 10.
\(\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+\ldots+\frac{1}{(3 n-1)(3 n+2)}=\frac{n}{(6 n+4)}\)
Answer:
Let given statement is p(n) where n ∈ N.
i.e.,

Thus, given statement is true for n = k + 1, i.e., p(k + 1) is true.
Therefore, by principal of mathematical induction given statement is true for all natural numbers n ∈ N.
Hence Proved

Question 11.
\(\frac{1}{1.2 .3}+\frac{1}{2.3 .4}+\frac{1}{3.4 .5}+\ldots .+\frac{1}{n(n+1)(n+2)} = \frac{n(n+3)}{4(n+1)(n+2)}\)
Answer:
Let given statement is p(n), where n ∈ N.

Thus, given statement is true for n = k + 1 i.e., p(k + 1) is also true.
Hence proved.

Question 12.
a + ar + ar² + ........ + ar^{n - 1} = \(\frac{a\left(r^n-1\right)}{r-1}\)
Answer:
Let given statement is p(n), where n ∈ N.
Thus,
P(n) = a + ar + ar² + ........ + ar^{n - 1} = \(\frac{a\left(r^n-1\right)}{r-1}\)
For n = 1
P(1) = a = \(\frac{a\left(r^1-1\right)}{r-1}=\frac{a(r-1)}{(r-1)}\) = a
Thus, given statement is true for n = 1, i.e., P(1) is true.
Again, let given statement is true for n = k i.e., P(k) is true.
Now P(k) = a + ar + ar² + .......+ ar^{k - 1}
= \(\frac{a\left(r^k-1\right)}{r-1}\) .............. (1)
Now, we will show that given statement is also true for n = k + 1 i.e., P(k + 1) is true.
Now, P(k + 1) = a + ar + ar² + ...... + ar^{k - 1} + ar^k

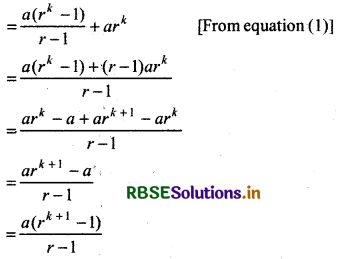
Thus, given statement is true for n = k + 1 i.e., p(k +1) is also true.
Thus, according to principal of mathematical induction, given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 13.
\(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots \left[1+\frac{(2 n+1)}{n^2}\right]\) = (n + 1)²
Answer:
Let given statement is P(n), where n ∈ N

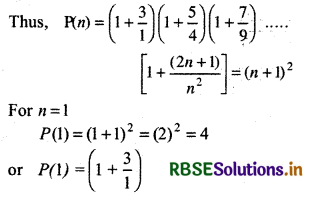
= 1 + 3 = 4 = (1 + 1)² = 4
Thus, given statement is true for n = 1, i.e., P(1) is true.
Again, let given statement is true for n = k, ie., P(k) is true.
Then P(k) = \(\left(1+\frac{3}{1}\right)\left(1+\frac{5}{4}\right)\left(1+\frac{7}{9}\right) \ldots\left[1+\frac{(2 k+1)}{k^2}\right]\) = (k + 1)² ............ (1)
Now, we will prove that given statement is true for n = k + 1 i.e., p(k + 1) is true.

Thus, given statement is true for n = k + 1, P(k + 1) is also true.
Thus, According to principal of mathematical induction we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 14.
\(\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right) \cdot \cdots\left(1+\frac{1}{n}\right)\) = (n + 1)
Answer:
Let given statement is P(n) where n ∈ N
Thus,

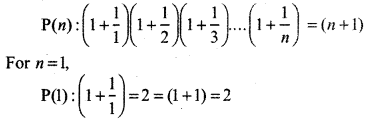
Thus, given statement is true for n = 1 i.e., p(1) is true.
Again, let given statement is true for n = k i.e., P(k) is true.
Then,
P(k): \(\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right) \ldots\left(1+\frac{1}{k}\right)\)
= (k + 1) ................ (1)

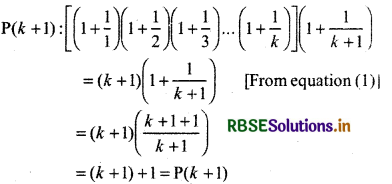
= (k + 1) + 1 = p(k + 1)
Thus, given statement is true for n = k + 1 i.e. is true.
Thus, according to principal of mathematical induction, we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 15.
1² + 3² + 5² + .......... + (2n - 1)² = \(\frac{n(2 n-1)(2 n+1)}{3}\)
Answer:
Let given statement is p(n), where n ∈ N.
Thus, P(n): 1² + 3² + 5² + ........ + (2n - 1)²
= \(\frac{n(2 n-1)(2 n+1)}{3}\)
When n=1, then
P(1): 1² = 1 = \(\frac{1(2 \times 1-1)(2 \times 1+1)}{3}\)
= \(\frac{(2-1)(2+1)}{3}\) = \(\frac{1 \times 3}{3}\) = 1 = 1²
Thus, given statement is true for n = 1 i.e., P(1) is true.
Again. Let given statement is true for n = k i.e.. P(k) is true, then
P(k) = 1² + 3² + 5² + ....... + (2k - 1)²
= \(\frac{k(2 k-1)(2 k+1)}{3}\) ......... (1)
Now we will show that given statement is true for n = k + 1 i.e., p(k + 1) is also true.
Now. p(k + 1):[1² + 3² + 5² + ............ + (2k - 1)²] + [2(k + 1) - 1]²

Thus, this statement is true for n = k + 1 where n ∈ N
Thus, given statement is true for n = k + 1 i.e., P(k + 1) is also true.
Therefore, according to principal of mathematical induction, we can see that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 16.
\(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+\ldots+\frac{1}{(3 n-2)(3 n+1)}=\frac{n}{(3 n+1)}\)
Answer:
Let given statement is P(n), where n ∈ N

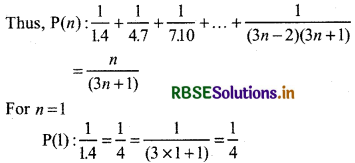
Thus, P(n) is true for n = 1.
i.e., P(1) is true.
Again, let P(n) is true for n = k.
i.e., P(k) is true, then

Thus, by principal of mathematical induction given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 17.
\(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\ldots+\frac{1}{(2 n+1)(2 n+3)}=\frac{n}{3(2 n+3)}\)
Answer:
Let given statement is P(n), where n ∈ N.
Thus,

Thus, given statement is true for n = k + 1 i.e., P(k + 1) is also true.
Therefore, By principal of mathematical induction we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 18.
1 + 2 + 3 + ........... + n < \(\frac{1}{8}\) (2n + 1)²
Answer:
Let given statement is P(n), where n ∈ N.
Thus, P(n): 1 + 2 + 3 + ....... + n < \(\frac{1}{8}\)(2n + 1)²
Now, for n = 1

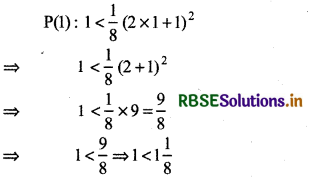
We see that given statement is true forn 1 i.e., P(l) is
true.
Again, let given statement is true for n = k i.e., P(k+ 1)
is also true.
Thus, P(k): 1 + 2 + 3 + ....... + k < \(\frac{1}{8}\)(2k + 1)² .............. (1)
Now, we will prove that given statement ¡s true for n = k +1 i.e., P(k + 1) is also true.

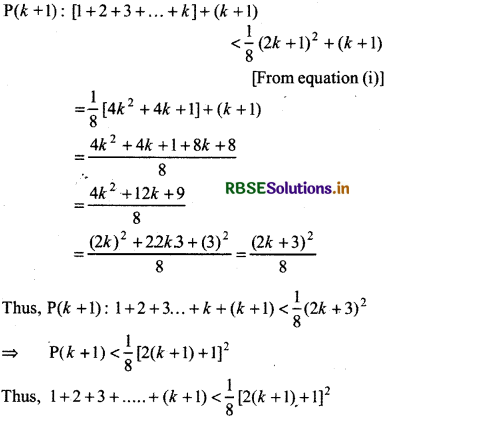
We see that given statement is true for n = k + 1 i.e., P(k + 1) is also true.
Therefore, by principal of mathematical we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 19.
n(n + 1)(n + 5), is a multiple of 3.
Answer:
Let given statement is p(n) where n ∈ N.
Then, p(n) = n(n + 1)(n + 5), is multiple of 3 for n = 1.
P(1) = 1(1 + 1)(l + 5), which is multiple of 3.
= 12.6 = 12
Thus, for n = 1, P(1) is true.
Again, let given statement is true for n = k i.e., P(k) is true, then
P(k) = k(k + 1) (k + 5) is a multiple of 3.
∴ k(k + 1) (k + 5) = 3p
⇒ k(k² + 6k + 5) = 3p
k³ + 6k² + 5k = 3p
or k² = 3p - 6k² - 5k ...... (1)
Now we will show that it is true.
For n = k +1 i.e.,
P(k + 1)= (k + 1) (k + 2) (k + 6) is also a multiple of 3.
P(k + 1) = (k² + 3k + 2) (k + 6)
⇒ k³ + 3k² + 2k + 6k² + 18k + 12
⇒ k³ + 9k² + 20k + 12
Put the value of k3 from eqn (1)
P(k + 1) = 3p - 6k² - 5k + 9k² + 20k + 12
⇒ 3p + 3k² + 15k + 12
⇒ 3(p + k² + 5k + 4) is divisible by 3.
Hence P(k + 1) is true.
Hence Proved

Question 20.
10^{2n - 1} + 1, is divisible by 11.
Answer:
Let given statement is P(n), where n ∈ N.
Then, P(n) :10^{2n - 1} + 1, is divisible by 11.
For n = 1
P(1) = 10^{2 × 1 - 1} + 1 = 10¹ + 1 = 11,
which is divisible by 11.
We see that given statement is true for n = 1 i.e., P(!) is true.
Again, let given statement is true for n = k
i.e., P(k) is true.
Then, P(k) = 10^{2k - 1} + 1, is divisible by 11 ...... (1)
Now, we will show that given statement is true for n = k + 1 i.e., P(k + 1) is true.
Then, P(k + 1) = 10^{2(k + 1) - 1} + 1
= 10^{2k + 2 - 1} + 1
= 100.10^{2k - 1} + 1
= (99 + 1)10^{2k - 1} + 1
= 99.10^{2k - 1} + 10^{2k - 1} + 1
= (10^{2k - 1} + 1) + 99.10^{2k - 1}
We see that R.H.S. has two term. Each term is divisible by 11. Since 99 is divisible by 11 so sum of two terms will be divisible by 11.
Thus, statement is true for n = k + 1 i.e., P(k + 1) is true.
Then by principle of mathematical induction we can say that statement is true for all natural numbers n ∈ N.
Hence Proved

Question 21.
x²ⁿ - y²ⁿ, is divisible by x + y.
Answer:
Let given statement is P(H), where n ∈ N.
Then, P(n) = x²ⁿ - y²ⁿ
For n = 1
P(1) = x² - y² = (x + y) (x - y), .
which is divisible by (x + y).
Thus, given statement is true for n = 1 i.e., P( 1) is true.
Again, let given statement is true for n = k i.e., P(k) is true.
Then, P(k) = x^2k - y^2k, is divisible by (x + y) .............. (1)
Now, we will show that P(n) is true for n = k + 1 i.e.,
P(k + 1) is true.
P(k + 1): = x^{2(k + 1)} - y^{2(k + 1)}
= x^{2k + 2} - y^{2k + 2}
= x^2k . x² - y^2k . y²
= x^2k . x² - y^2k . y² + x² y^2k - x² y^2k
(By adding and subtracting x²y^2k)
= x²x^2k - x²y^2k + x²y^2k - y^2k.y²
= x²(x^2k - y^2k) + y^2k(x² - y²)
= (x^2k - y^2k)x² +(x - y) (x + y) y^2k
We see that there are two terms in R.H.S. In first term x^2k - y^2k is divisible by x + y and other term Will also be divisible by x + y then sum of two term will be divisible by x + y. Thus, given statement will be true for n = k + 1 i.e., P(k +1) is true. Thus, by principle of mathematical induction we can say that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 22.
3^{2n + 2} - 8n - 9, is divisible by 8.
Answer:
Let given statement is P(n), where n ∈ N.
Thus, P(n) = 3^{2n + 2} - 8n - 9, is divisible by 8.
For n = 1 .
P(1) = 3^{2 × 1 + 2} - 8 × 1 - 9
= 3⁴ - 8 - 9
= 81 - 8 - 9
= 81 - 17 = 64, which is divisible by 8.
Thus, given statement is true for n = 1 i.e., P(1) is true.
Again, let given statement is true for n = k i.e., P(k) is true, then
If P(k) = 3^{2k + 2} - 8k - 9, is divisible by 8. .......... (1)
Now, we will show that P(n) is true for n = k + 1 i.e., P(k +1) is true, then
P(k + 1) = 3^{2(k + 1) + 2} - 8(k + 1) - 9
= 3^{2k + 2 + 2} - 8(k + 1) - 9
= 3^{2k + 2} . 3² - 8k - 8 - 9
= 93^{2k + 2} - 8k - 17
= (8 + 1)3^{2k + 2} - 8k - 9 - 8
= 83^{2k + 2} + (3^{2k + 2} - 8k - 9) - 8
= 83^{2k + 2} + P(k) - 8 [From equation (i)]
= (8.3^{2k + 2} - 8) + P(k) {where P(k) = 3^{2k + 2} - 8k - 9}
= 8(3^{2k + 2} - 1) + P(k)
We see that first and second term of R.H.S. is divisible by 8 so sum of the two terms will also be divisible by 8. Thus, given statement is true for n = k + 1 i.e., P(k +1) is true.
Thus, by principle of mathematical induction given statement is true for all natural numbers n ∈ N.
Hence Proved

Question 23.
41ⁿ - 14ⁿ, is a multiple of 27.
Answer:
Let given statement is P(n), where n ∈ N
Thus, P(n) = 41¹ - 14¹, is multiple of 27.
For n = 1 P(1) = 41¹ - 14¹
= 41 - 14 = 27,
which is multiple of 27.
We see that given statement is true for n = 1 i.e., P(1) is true. Again, let given statement is true for n = k i.e., P(k) is true. ,
Then, P(k) = 41^k - 14^k , is multiple of 27. ....... (1)
Now, we will show that given statement is true for n = k + 1 i.e., P(k + 1) is also true.
Now, P(k + 1) = 41^{k + 1} - 14^{k + 1}
= 41^{k + 1} - 41.14^k + 41.14^k - 14^k + 1 (By adding and subtracting 41.14^k)
= 41^k . 41 - 41.14^k + 41.14^k - 14^k . 14
= 41(41^k - 14^k) + 14^k (41 - 14)
= 41(41^k - 14^k) + 27.14^k
Here, there are two terms in R.H.S. In first term (41^k -14^k) is multiple of 27 (from equation 1). Thus 41 (41^k - 14^k) will also be multiple of 27. In second term 27 is a factor, thus second term will be multiple of 27. Then sum of two terms will be multiple of 27. Therefore, by principle of mathematical induction we can see that given statement is true for all natural numbers n ∈ N.
Hence Proved.

Question 24.
(2n + 7) < (n + 3)²
Answer:
Let given statement is P(n), where n ∈ N.
Then, P(n) = (2n + 7) < (n + 3)²
For n = 1
P(1): (2 × 1 + 7) = 9 < (1 + 3)² = 16
9 < 16
Thus, given statement is true for n = 1 i.e.,P(1) is true.
Again, let given statement is true for n = k P(k) is true.
Then, P(k):(2k + 7) < (k + 3)² ........... (i)
For n = k + 1
P(k + 1) : 2(k + 1) + 7 < (k + 1 + 3)²
⇒ (2k + 1) < (k + 4)²
⇒ (2k + 9) < (k² + 8k + 16) ............. (ii)
Now, from (i) equation
2k + 7 < (k + 3)²
2k + 7 < k² + 6k + 9
2k + 7 + 2 < k² + 6k + 9 + 2
2k + 9 < k² + 6k + 11 ................ (iii)
From (ii) and (iii) it is clear that
2k + 9 < k² + 8k + 16
Hence P(k + 1) is true.
Hence Proved.