RBSE Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 3 Trigonometric Functions Miscellaneous Exercise

Question 1.
Prove that 2cos\(\frac{\pi}{13}\)cos\(\frac{9 \pi}{13}\) + cos\(\frac{3 \pi}{13}\) + cos\(\frac{5 \pi}{13}\) = 0.
Answer:
L.H.S = 2cos\(\frac{\pi}{13}\)cos\(\frac{9 \pi}{13}\) + cos\(\frac{3 \pi}{13}\) + cos\(\frac{5 \pi}{13}\)

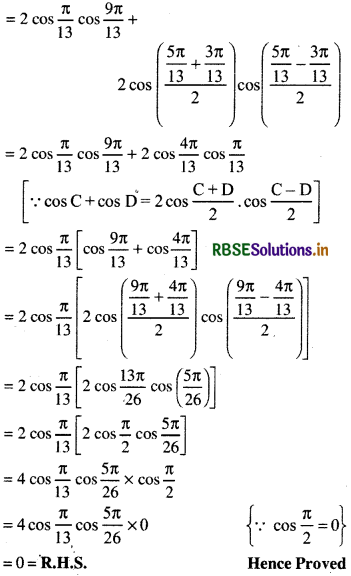
Question 2.
Prove that:
(sin 3x + sin x)sin x + (cos 3x - cos x) cos x = 0
Answer:
L.H.S. = (sin 3x + sin x) sin x +(cos 3x - cos x) cos x
= sin 3x sin x + sin² x + cos3x cosx - cos² x
= cos 3x cos x + sin 3x sin x + sin²x - cos² x
= cos(3x - x) - (cos² x - sin² x)
=cos2x - cos2x
(Using formula cos 2A = cos²A - sin²A)
= O = R.H.S. Hence Proved

Question 3.
Prove that:
(cos x + cos y)² + (sin x - sin y)² = 4cos²\(\frac{x+y}{2}\)
L,H.S. = (cos x + cos y)² +(sin x - sin y)²
= cos² x + cos² y + 2cosxcosy + sin²x + sin²y - 2sinxsiny
= (cos²x + sin²x) + (cos²y + sin²y) + 2cos x cos y - 2sinx siny
= 1 + 1 + 2(cos x cosy - sin x sin y) {∵ cos²θ + sin²θ = 1)
= 2 + 2cos (x + y)
= 2[1 + cos(x + y)]
= 2[1 + 2cos²\(\left(\frac{x+y}{2}\right)\) - 1]
[Using formula cos x = 2 cos²\(\frac{x}{2}\) - 1]
= 2 × 2 cos²\(\frac{x+y}{2}\)
= 4 cos²\(\frac{x+y}{2}\)
= R.H.S
Hence Proved

Question 4.
Prove that
(cos x - cos y)² + (sin x - sin y)² = 4sin²
Answer:
L.H.S. = (cos x - cos y)² ± (sin x - sin y)²
= cos x + cos y - 2cosx cos y + sin²x + sin²y - 2sinx siny
=(cos²x + sin²x) + (cos²y + sin²y) - 2cosx cosy - 2sinx sin y
= 1 + 1 - 2[cosx cosv+ sin x sin y] {From cos²θ + sin²θ = 1)
= 2 - 2 [cos (x - y)]
= 2[1 - cos(x - y)]

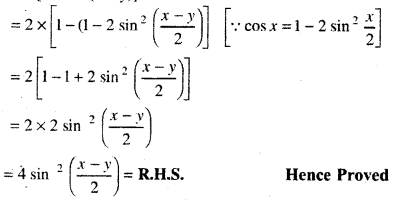
Question 5.
Prove that
sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Answer:
L.H.S = sin x + sin 3x + sin 5x + sin 7x
= (sin 7x + sin x) + (sin 5x + sin 3x)
= 2sin\(\frac{7 x+x}{2}\)cos\(\frac{7 x-x}{2}\) + 2sin\(\frac{5 x+3x}{2}\)cos\(\frac{5 x-3x}{2}\)
[Using formula sin A + sin B = 2 sin\(\frac{A+B}{2}\)cos\(\frac{A-B}{2}\)]
= 2sin\(\frac{8 x}{2}\)cos\(\frac{6 x}{2}\) + 2sin\(\frac{8 x}{2}\)cos\(\frac{2 x}{2}\)
= 2sin 4x.cos 3x + 2sin 4x cos x
= 2sin 4x[cos 3x + cos x]
= 2sin 4x[2 cos\(\frac{3 x+x}{2}\)cos\(\frac{3 x+x}{2}\)]
[Using formula cosx + cosy = 2cos\(\frac{x+y}{2}\)cos\(\frac{x-y}{2}\)]
= 2sin 4x[2 cos\(\frac{4 x}{2}\)cos\(\frac{2 x}{2}\)]
= 4sin 4x cos 2x cos x
= 4 cos x cos 2x sin 4x
= R.H.S
Hence Proved.

Question 6.
Prove that:
\(\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\cos 5 x)+(\cos 9 x+\cos 3 x)}\) = tan 6x
Answer:

Question 7.
Prove that:
sin 3x + sin 2x - sin x = 4sin x cos \(\frac{x}{2}\) cos \(\frac{3x}{2}\)
Answer:
L.H.S = sin 3x + sin 2x - sin x

Find sin\(\frac{x}{2}\), cos\(\frac{x}{2}\) and tan\(\frac{x}{2}\) in each of the following question.

Question 8.
tan x = -\(\frac{4}{3}\), x is second quadrant.
Answer:
tan x = -\(\frac{4}{3}\), x lies second quadrant.
90° < x < 180° ⇒ 45° < \(\frac{x}{2}\) < 90°

Thus, \(\frac{x}{2}\) will lies in first quadrant so, all trigonometric ratios of \(\frac{x}{2}\) will be positive.

Thus required value of tan\(\frac{x}{2}\) will be 2, since \(\frac{x}{2}\) will lie in first quadrant in which all trigonometric ratios are positive so tan \(\frac{x}{2}=-\frac{1}{2}\) is negligible.
Required value of = 2

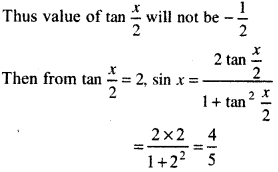
Thus, sin x = \(\frac{4}{2}\) which is positive since. It is given that x lies in second quadrant in which sin x is positive.

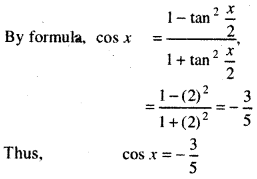
(Since, x lies in second quadrant in which cos x is negative)

Only positive value will be considered since \(\frac{x}{2}\) lies in first quadrant.
Thus, sin \(\frac{x}{2}=\frac{2}{\sqrt{5}}\), cos \(\frac{x}{2}=\frac{1}{\sqrt{5}}\) and tan \(\frac{x}{2}\) = 2 are required values.

Question 9.
cos x = -\(\frac{1}{3}\), x in third quadrant.
Answer:
cos x = -\(\frac{1}{3}\)
180° < x < 270°
[∵ given that x lies in third quadrant. In this will be positive.]

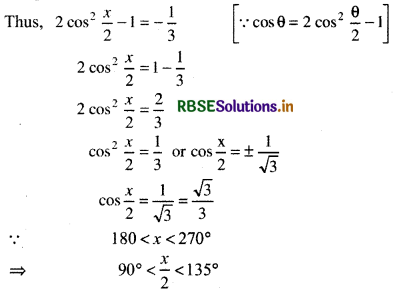
Thus, \(\frac{x}{2}\) will be in second quadrant is negligible since \(\frac{x}{2}\) lies in second quadrant so cos \(\frac{x}{2}\) will be negative.

[Since \(\frac{x}{2}\) lies in second quadrant so sin \(\frac{x}{2}\) will be positive]

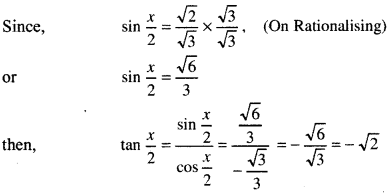
Since, x lies in third quadrant so value of x lies between π and \(\frac{3 \pi}{2}\).
i.e., π < x < \(\frac{3 \pi}{2}\)
Then, value of \(\frac{x}{2}\) will be between \(\frac{\pi}{2}\) and \(\frac{3 \pi}{2}\).
i.e \(\frac{\pi}{2}\)< \(\frac{x}{2}\) <\(\frac{3 \pi}{4}\)

Thus, will lies in second quadrant so that sin will be +ve and cos\(\frac{x}{2}\). and tan \(\frac{x}{2}\) will be negative.
then sin \(\frac{x}{2}=\frac{\sqrt{6}}{3}\), and cos \(\frac{x}{2}=-\frac{\sqrt{3}}{3}\)
and tan\(\frac{x}{2}\) = -√2
Thus,sin \(\frac{x}{2}=\frac{\sqrt{6}}{3}\), cos \(\frac{x}{2}=-\frac{\sqrt{3}}{3}\) and tan \(\frac{x}{2}\) = -√2

Question 10.
sin x = \(\frac{1}{4}\), x in second quadrant.
Answer:
sin x = \(\frac{1}{4}\), [Using formula sin²x + cos²x = 1]

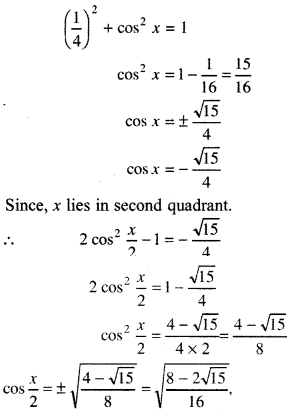
Since \(\frac{x}{2}\) will lie in first quadrant.
Since, x lie is second quadrant.
Thus \(\frac{\pi}{2}\) < x < π
\(\frac{\pi}{4}<\frac{x}{2}<\frac{\pi}{2}\)

\(\frac{x}{2}\) will lie in first quadrant then all trigonometric ratio will be always positive.

Thus, sin\(\frac{x}{2}=\frac{\sqrt{8+2 \sqrt{15}}}{4}\), cos\(\frac{x}{2}=\frac{\sqrt{8-2 \sqrt{15}}}{4}\) and tan\(\frac{x}{2}=4+\sqrt{15}\) are required values.