RBSE Solutions for Class 11 Maths Chapter 3 त्रिकोणमितीय फलन Ex 3.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 3 त्रिकोणमितीय फलन Ex 3.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.3

सिद्ध कीजिए-

प्रश्न 1.
sin²\(\frac{\pi}{6}\) + cos²\(\frac{\pi}{3}\) - tan²\(\frac{\pi}{4}\) = - \(\frac{1}{2}\).
हल:
प्रश्नानुसार L. H.S.

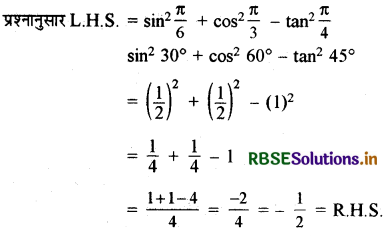
प्रश्न 2.
2 sin²\(\frac{\pi}{6}\) + cosec²\(\frac{7 \pi}{6}\) cos²\(\frac{\pi}{3}\) = \(\frac{3}{2}\)
हल:

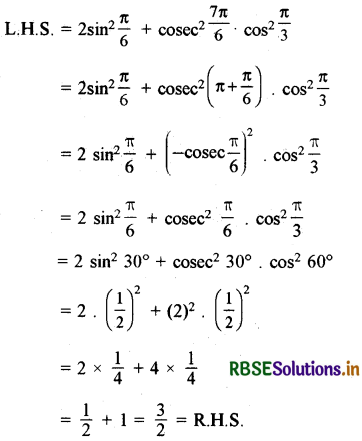
प्रश्न 3.
cot²\(\frac{\pi}{6}\) + cosec \(\frac{5 \pi}{6}\) . 3 tan² \(\frac{\pi}{6}\) = 6
हल:

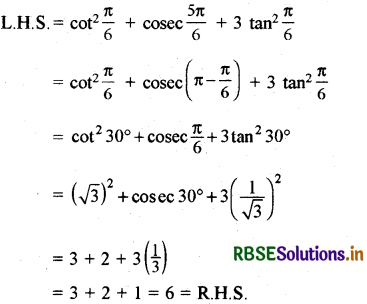
प्रश्न 4.
2sin²\(\frac{3 \pi}{4}\) + 2cos²\(\frac{\pi}{4}\) + 2sec²\(\frac{\pi}{3}\)
हल:

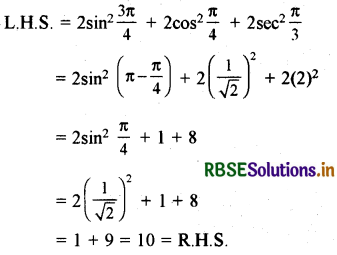
प्रश्न 5.
मान ज्ञात कीजिए—
(i) sin 75°
हल:
∵ sin 75° = sin(45° + 30°)
= sin 45°. cos 30° + cos 45°. sin 30°

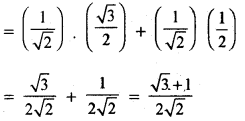
(ii) tan 15°
हल:
tan 15° = tan (45° - 30°)

प्रश्न 6.
निम्नलिखित को सिद्ध कीजिए-
cos(\(\frac{\pi}{4}\) - x) cos(\(\frac{\pi}{4}\) - y) - sin(\(\frac{\pi}{4}\) - x) sin(\(\frac{\pi}{4}\) - y) = sin (x + y)
हल:
L.H.S. = cos(\(\frac{\pi}{4}\) - x) cos(\(\frac{\pi}{4}\) - y) - sin(\(\frac{\pi}{4}\) - x) sin(\(\frac{\pi}{4}\) - y)
माना \(\frac{\pi}{4}\) - x = A तथा \(\frac{\pi}{4}\) - y = B
∴ = cos A. cos B - sin A. sin B
cos (A + B)
A तथा B का मान रखने पर

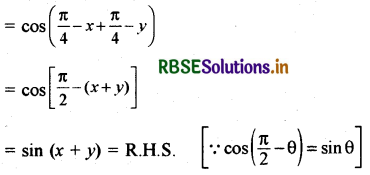
प्रश्न 7.
\(\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}\) = \(\left(\frac{1+\tan x}{1-\tan x}\right)^2\)
हल:

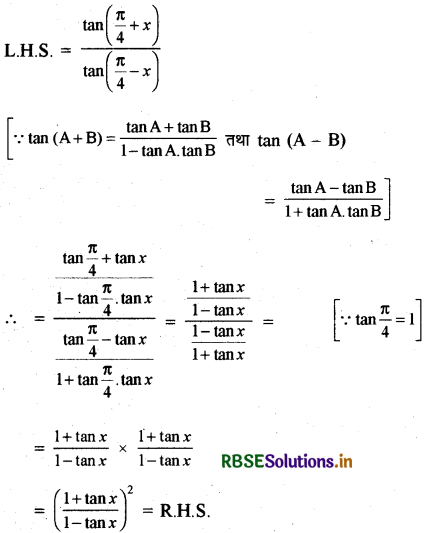
प्रश्न 8.
\(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}-x\right)}\) = cot²x
हल:

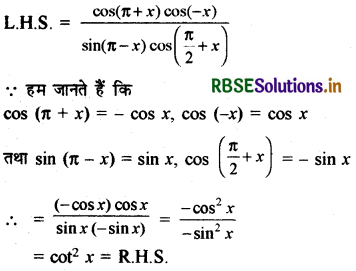
प्रश्न 9.
cos (\(\frac{3 \pi}{2}\) + x) cos (2π + x) [cot (\(\frac{3 \pi}{2}\) - x) + cot (2π + x)] = 1
हल:

प्रश्न 10.
sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x = cos x
हल:
L.H.S. = sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x
माना कि (n + 1)x = A तथा (n + 2) x = B
∴ = sin A. sin B + cos A cos B
= cos (A - B)
A तथा B का मान रखने पर
= cos [(n + 1)x - (n + 2)x]
= cos (nx + x - nx - 2x]
= cos (x - 2x) = cos (-x)
हम जानते हैं कि cos (-θ) = cos θ ∀ θ ∈ R
∴ = cos x
= R.H.S.

प्रश्न 11.
cos (\(\frac{3 \pi}{4}\) + x) - cos (\(\frac{3 \pi}{4}\) - x) = - √2 sin x
हल:

प्रश्न 12.
sin² 6x - sin² 4x = sin 2x sin 10x
हल:
L.H.S.= sin² 6x - sin² 4x
= (sin 6x + sin 4x) (sin 6x - sin 4x) [∵ a² - b² = (a + b) (a - b)]

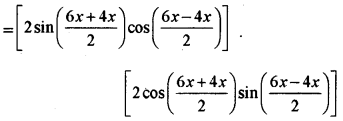
= (2 sin 5x cos x) (2 cos 5x . sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x . sin 2x (∵ 2 sin θ cos θ = sin 2θ)
R.H.S.

IInd Method :
L.H.S.= sin²6x - sin²4x
= sin (6x + 4x) sin (6x - 4x)
[∵ sin²A sin²B = sin(A + B) sin(A - B)]
= sin 10x sin 2x = R.H.S.

प्रश्न 13.
cos² 2x cos² 6x = sin 4x sin 8x
हल:
L.H.S. = cos² 2x - cos² 6x
= 1 - sin² 2x - (1 - sin² 6x)
= - sin² 2x + sin² 6x
= sin² 6x - sin² 2x
माना कि 6x = A तथा 2x = B अतः
सूत्र sin² A - sin² B = sin (A + B) sin (A - B) के अनुसार
L.H.S.= sin² 6x - sin² 2x
= sin (6x + 2x). sin (6x - 2x)
= sin 8x sin 4x
= sin 4x sin 8x = R.H.S.

प्रश्न 14.
sin 2x + 2 sin 4x + sin 6x = 4 cos² x sin 4x
हल:
L.H.S. = sin 2x + 2 sin 4x + sin 6x
= (sin 2x + sin 6x) + 2 sin 4x
= 2 sin \(\left(\frac{2 x+6 x}{2}\right)\) cos \(\left(\frac{2 x-6 x}{2}\right)\) + 2 sin 4x
[∵ sin A + sin B = 2 sin \(\frac{A+B}{2}\) cos \(\frac{\mathrm{A}-\mathrm{B}}{2}\)]
= 2 sin (4x) cos (-2x) + 2 sin 4x
= 2 sin 4x (cos 2x + 1) [∵ cos (- x) = cos x ∀ x ∈ R]
= 2 sin 4x (2 cos² x) [∵ cos 2x = 2 cos²x - 1]
= 4 cos² x sin 4x
= R.H.S.

प्रश्न 15.
cot 4x (sin 5x + sin 3x) = cot x (sin 5x - sin 3x)
हल:
L.H.S. cot 4x (sin 5x + sin 3x)

प्रश्न 16.
\(\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}\) = - \(\frac{\sin 2 x}{\cos 10 x}\)
हल:

प्रश्न 17.
\(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}\) = tan 4x
हल:

प्रश्न 18.
\(\frac{\sin x-\sin y}{\cos x+\cos y}\)
हल:

प्रश्न 19.
\(\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x}\) = tan 2x
हल:

प्रश्न 20.
\(\frac{\sin x-\sin 3 x}{\sin ^2 x-\cos ^2 x}\) = 2 sin x
हल:

प्रश्न 21.
\(\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x}\) = cot 3x
हल:

प्रश्न 22.
cot x cot 2x - cot 2x cot 3x - cot 3x cot x = 1
हल:
माना 3x = x + 2x
⇒ cot 3x = cot (x + 2x)
∴ cot 3x = \(\frac{\cot x \cot 2 x-1}{\cot 2 x+\cot x}\)
∵ cot (A + B) = \(\frac{\cot A \cot B-1}{\cot B+\cot A}\)
⇒ cot 3x cot 2x + cot 3x cot x = cot x cot 2x - 1
⇒ cot x cot 2x - cot 2x cot 3x - cot x cot 3x = 1
L.H.S. = R.H.S.

प्रश्न 23.
tan 4x = \(\frac{4 \tan x\left(1-\tan ^2 x\right)}{1-6 \tan ^2 x+\tan ^4 x}\)
हल:
L.H.S. tan 4x = tan 2 (2x)

प्रश्न 24.
cos 4x = 1 - 8 sin² x cos² x
हल:
L.H.S.= cos 4x = 1 - 2 sin² 2x = 1 - 2[sin 2x]²
= 1 - 2[2 sin x cos x]²
= 1 - 2[4 sin2 x cos2 x]
= 1 - 8 sin² x cos² x
= R.H.S.

प्रश्न 25.
cos 6x = 32 cos⁶ x 48 cos⁴ x + 18 cos² x - 1
हल:
L.H.S. = cos 6x = cos 2(3x)
= 2 cos² 3x - 1
= 2 (4 cos³ x - 3 cos x)² - 1
∵ cos 3x = (4 cos³x - 3 cos x)
= 2 [16 cos⁶ x - 2 (4 cos³ x) (3 cos x) + 9 cos² x] - 1
= 2 (16 cos⁶ x - 24 cos⁴ x + 9 cos² x) - 1
= 32 cos⁶ x - 48 cos⁴ x + 18 cos²x - 1
= R.H.S.