RBSE Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 3 Trigonometric Functions Ex 3.3

Question 1.
Prove that:
sin²\(\frac{\pi}{6}\) + cos²\(\frac{\pi}{3}\) - tan²\(\frac{\pi}{4}\) = \(\frac{1}{2}\)
Answer:
L.H.S = sin²\(\frac{\pi}{6}\) + cos²\(\frac{\pi}{3}\) - tan²\(\frac{\pi}{4}\)

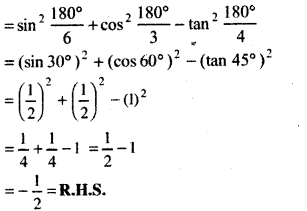
Hence Proved.

Question 2.
Prove that:
2sin²\(\frac{\pi}{6}\) + cosec²\(\frac{7 \pi}{6}\)cos²\(\frac{\pi}{3}\) = \(\frac{3}{2}\)
Answer:
L.H.S = 2sin²\(\frac{\pi}{6}\) + cosec²\(\frac{7 \pi}{6}\)cos²\(\frac{\pi}{3}\)

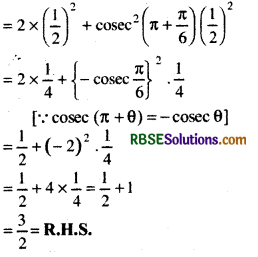
Question 3.
Prove that:
cot²\(\frac{\pi}{6}\) + cosec\(\frac{5 \pi}{6}\) + 3tan²\(\frac{\pi}{6}\) = 6
Answer:
L.H.S = cot²\(\frac{\pi}{6}\) + cosec\(\frac{5 \pi}{6}\) + 3tan²\(\frac{\pi}{6}\)
= (√3)² + cosec(π - \(\frac{\pi}{6}\)) + 3 × \(\left(\frac{1}{\sqrt{3}}\right)^2\)
= 3 + (cosec \(\frac{\pi}{6}\)) + 3 × \(\frac{1}{3}\)
[ cosec(π - θ) = cosec θ]
= 3 + 2 + 1
= 6
= R.H.S
Hence Proved

Question 4.
Prove that:
2sin²\(\frac{3 \pi}{4}\) + 2 cos²\(\frac{\pi}{4}\) + 2sec²\(\frac{\pi}{3}\) = 10
Answer:
L.H.S = 2sin²\(\frac{3 \pi}{4}\) + 2 cos²\(\frac{\pi}{4}\) + 2sec²\(\frac{\pi}{3}\)

Question 5.
Find the value of:
(i) sin 75°
Answer:
sin 75° = sin(45° + 30°)
= sin 45° .cos 30° + cos 45° sin 30°
(∵ sin(A + B) = sin A cos B + cos A sin B)

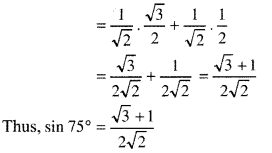
(ii) tan 15°
Answer:
tan 15° = tan(45° - 30°)
[∵ 15° = 45° - 30°)

Question 6.
Prove the following:
cos(\(\frac{\pi}{4}\) - x)cos(\(\frac{\pi}{4}\) - y) - sin(\(\frac{\pi}{4}\) - x)sin(\(\frac{\pi}{4}\) - y) = sin(x + y)
Answer:

Question 7.
Prove the following
\(\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}=\left(\frac{1+\tan x}{1-\tan x}\right)^2\)
Answer:

Question 8.
Prove the following:
\(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}\) = cot²x
Answer:
L.H.S = \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}\)
= \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}\)
[Formula cos(π + θ) = -cos θ, cos(-θ) = cos θ and from sin(π - θ) = sin θ, cos(π + θ) = -sin θ]

Question 9.
Prove the following:
cos(\(\frac{3 \pi}{2}\) + x) cos(2π + x) × [cot (\(\frac{3 \pi}{2}\) - x) + cot(2π + x)] = 1
Answer:
L.H.S = cos(\(\frac{3 \pi}{2}\) + x) cos(2π + x) × [cot (\(\frac{3 \pi}{2}\) - x) + cot(2π + x)]
= sin x × cos x[tan x + cot x]
[∵ cos(\(\frac{3 \pi}{2}\) + x) = sin x, cos(2π + x) = cos x]
[∵ cot(\(\frac{3 \pi}{2}\) - x) = tan x, cot(2π + x) = cot x]
= sin x cos x\(\left[\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right]\)
= sin x cos x.\(\frac{\sin x}{\cos x}\) + sin x cos x \(\frac{\cos x}{\sin x}\)
= sin²x + cos²x [∵ sin²θ + cos²θ = 1]
= 1 = R.H.S
Hence Proved.

Question 10.
Prove the following :
sin (n + 1)x sin (n + 2)x + cos(n + 1)x cos(n + 2)x = cos x
Answer:
L.H.S. = sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x
= cos (n +1) x cos (n + 2)x + sin (n +1) x × sin (n + 2) x [By the formula cos(x - y) = cos x cos y + sin x sin y]
= cos [(n + 1)x - (n + 2) x]
= cos [nx + x - nx - 2x]
= cos (-x) = cos x = R.H.S.
Hence Proved

Question 11.
Prove the following:
cos(\(\frac{3 \pi}{4}\) + x) - cos(\(\frac{3 \pi}{4}\) - x) = -√2 sin x
Answer:
L.H.S = cos(\(\frac{3 \pi}{4}\) + x) - cos(\(\frac{3 \pi}{4}\) - x)

Hence Proved

Question 12.
Prove the following:
sin²6x - sin²4x = sin 2x sin 10x
Answer:
L.H.S = sin²6x - sin²4x
= \(\frac{1}{2}\)[2sin²6x - 2sin²4x]
[By multiplying and dividing by 2]
= \(\frac{1}{2}\)[(1 - cos 12x) - (1 - cos 8x)] [∵ 2sin²θ = 1 - cos 2θ]
= \(\frac{1}{2}\)[1 - cos12x - 1 + cos 8x]
= \(\frac{1}{2}\)[cos 8x - cos 12x]
= \(\frac{1}{2}\)[2 sin\(\frac{8 x+12 x}{2}\) sin\(\frac{12 x-8 x}{2}\)
[∵ cos x - cos y = 2 sin\(\frac{x+y}{2}\) sin\(\frac{y - x}{2}\)]
= \(\frac{1}{2}\) [2sin\(\frac{20x}{2}\).sin\(\frac{4x}{2}\)]
= sin 10x sin 2x
= sin 2x sin 10x = R.H.S
Hence Proved

Second Method or Alternative method:
L.H.S = cos²2x - cos² 6x
= (cos 2x + cos 6x) (cos 2x - cos 6x)
By formula
[∵ a² - b² = (a + b)(a - b)]
= [2cos\(\frac{8 x}{2}\)cos\(\left(\frac{-4 x}{2}\right)\)].(2sin\(\frac{8 x}{2}\)sin\(\frac{4 x}{2}\))
[By formula cos x + cos y = 2 cos\(\frac{x+y}{2}\) cos\(\frac{x-y}{2}\)
and cos x - cos y = 2 sin \(\frac{x+y}{2}\) sin \(\frac{y-x}{2}\)]
= (2 cos 4x cos 2x) . (2 sin 4x sin 2x)
[∵ cos(-θ) = cos θ]
= (2 sin 4x cos 4x).(2 sin 2x cos 2x)
= sin 8x sin 4x [∵ sin 2θ = 2sin θ cos θ]
= sin 4x sin 8x = R.H.S
Hence Proved

Question 14.
Prove the following:
sin 2x + 2sin 4x + sin 6x = 4 cos²x sin 4x
Answer:
L.H.S = sin 2x + 2sin 4x + sin 6x
= (sin 2x + sin 6x) + 2 sin 4x
= 2sin\(\frac{2 x+6 x}{2}\)cos\(\frac{2 x-6 x}{2}\) + 2 sin 4x
(By formula sin x + sin y = 2 sin\(\frac{x+y}{2}\)cos\(\frac{x-y}{2}\))
= 2 sin \(\frac{8x}{2}\)cos\(\left(\frac{-4 x}{2}\right)\) + 2sin 4x
= 2 sin 4x cos (- 2x) + 2 sin 4x
= 2 sin 4x [cos 2x +1 ] [∵ cos (-θ) = cos θ]
= 2 sin 4x (2 cos²x - 1 + 1)
(∵ cos 2θ = 2 cos²θ - 1)
= 2 sin 4x × 2 cos2 x
= 4 cos2 x sin 4x = R.H.S.
Hence Proved

Question 15.
Prove the following :
cot 4x (sin 5x + sin 3x) = cot x (sin 5x - sin 3x)
Answer:
L.H.S. = cot 4x (sin 5x + sin 3x)

= \(\frac{\cos x}{\sin x}\)[2 cos 4x siin x]
= 2cos 4x cos x ............(ii)
From (i) and (ii)
cot 4x(sin 5x + sin 3x) = cot x(sin 5x - sin 3x)
L.H.S = R.H.S
Hence Proved

Question 16.
Prove the following:
\(\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=-\frac{\sin 2 x}{\cos 10 x}\)
Answer:

Question 17.
Prove the following:
\(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}\) = tan 4x
Answer:

Question 18.
Prove the following:
\(\frac{\sin x-\sin y}{\cos x+\cos y} \)= tan \(\frac{x-y}{2}\)
Answer:

Question 19.
Prove the following:
\(\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x}\) = tan 2x
Answer:

Question 20.
Prove the following:
\(\frac{\sin x-\sin 3 x}{\sin ^2 x-\cos ^2 x}\) = 2 sin x
Answer:

Question 21.
Prove the following:
\(\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x}\) = cot 3x
Answer:

Question 22.
Prove the following:
cot x cot 2x - cot 2x cot 3x - cot 3x cot x = 1
Answer:
cot 3x = cot(x + 2x)
cot 3x = \(\frac{\cot x \times \cot 2 x-1}{\cot 2 x+\cot x}\)
cot 3x (cot 2x + cot x) = cot x × cot 2x -1
(By cross-multiplication)
cot 3x cot 2x + cot 3x cot x = cot x × cot 2x - 1
1 = cot x × cot 2x - cot 2x cot 3x - cot 3x cot x
cot x cot 2x - cot 2x cot 3x - cot 3x cot x = 1
L.H.S. = R.H.S.
Hence Proved.

Question 23.
Prove the following:
tan 4x = \(\frac{4 \tan x\left(1-\tan ^2 x\right)}{1-6 \tan ^2 x+\tan ^4 x}\)
Answer:
L.H.S = tan 4x = tan2(2x)

Question 24.
Prove the following:
cos 4x = 1 - 8sin² x cos² x
Answer:
L.H.S = cos 4X = cos 2 (2x) [cos 2θ = 1 - 2 sin² θ] = 1 - 2 sin² 2x
= 1 - 2(2 sin x cos x)² [∵ sin 2x = 2 sin x cos x]
= 1 - 2 × 4 sin²x cos²x
= 1 - 8sin²x cos²x
= R.H.S
Hence proved

Question 25.
Prove the following:
cos 6x = 32cos⁶x - 48cos⁴x + 18cos²x - 1
Answer:
L.H.S = cos 6x
= cos³(2x) [∵ cos 3x = 4 cos³x - 3 cos x]
= 4cos³ 2x - 3 cos 2x
= cos 2x (4cos²2x - 3)
= cos2x [4 (cos 2x)² - 3) [v cos 2A = 2cos²x - 1]
= cos 2x [4 (2 cos 2 x - 1)² - 3] .
= cos 2x [4 (4 cos4 x + 1 - 4 cos2 x) -3]
= cos2x (16cos 4 x + 4 - 16cos² x - 3)
= (2 cos² x - 1) (16 cos⁴ x + 4 - 16 cos² x - 3)
= 32cos⁶ x + 8cos² x - 32cos⁴x - 6cos² x - 16cos⁴x - 4 + 16cos²x + 3
= 32cos⁶x - 48 cos⁴ x +18 cos² x - 1
= R.H.S.
Hence Proved.