RBSE Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 3 Trigonometric Functions Ex 3.2

Find the values of other five trigonometric functions. In exercise 1 to 5.

Question 1.
cos x = \(\frac{1}{2}\), x lies in third quadrant.
Answer:
We have cos x = -\(\frac{1}{2}\) and x lies in third quadrant
Thus, sec x = -\(\frac{2}{1}\) = -2
Now sin²x + cos²x = 1
or sin²x = 1 - cos²x = 1 - \(\frac{1}{4}=\frac{3}{4}\)
∴ sin x = ±\(\frac{\sqrt{3}}{2}\)
(If x Lies in third quadrant than 180° ≤ x ≤ 270°, (π ≤ x ≤ \(\frac{3}{2}\)π) Thus, here only tan and cot will be positive all other trigonometric functions will be negative) Since x lies in third quadrant so value ofsin x will be negative, Thus,

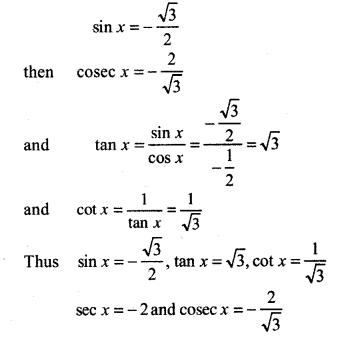
Question 2.
sin x = \(\frac{3}{5}\), x lies in second quadrant.
Answer:
Given, sin x = \(\frac{3}{5}\), and cosec x = \(\frac{5}{3}\)
since, sin²x + cos²x = 1
or cos²x = 1 - sin²x
= 1 - \(\left(\frac{3}{5}\right)^2\) = 1 - \(\frac{9}{25}\) or
cos²x = \(\frac{16}{25}\)
∴ cos x = ±\(\frac{4}{5}\)
For second quadrant 90° ≤ x ≤ 180°(\(\frac{\pi}{2}\) ≤ x ≤ π), in this sin x and cosec x will be positive rest will be negative according to ASTC
Since, x lies in second quadrant
Thus, cos will be negative

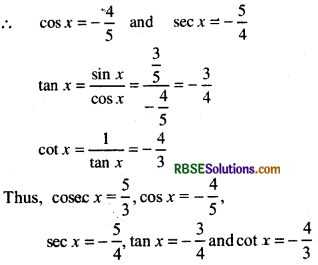
Question 3.
cot x = \(\frac{3}{4}\), x lies in third quadrant.
Answer:
cot x = \(\frac{3}{4}\), so tan x = \(\frac{4}{3}\)
cosec²x = 1 + cot²x
= 1 + \(\left(\frac{3}{4}\right)^2\) = 1 + \(\frac{9}{16}=\frac{25}{16}\)
∴ cosec x = ±\(\frac{4}{5}\)

(According to ASTC law, In third quadrant, except trigonometric functions of tan and cot all other trigonometric function will be negative)
cosec x = -\(\frac{5}{4}\) then sin x = -\(\frac{4}{5}\)
Now, cos²x + sin²x = 1
cos²x = 1 - sin²x
= 1 - \(\frac{16}{25}=\frac{9}{25}\)
cos x = ±\(\frac{3}{5}\)

In third quadrant, cos is negative
Thus, cos x = -\(\frac{3}{5}\) then sec x = -\(\frac{5}{3}\)
Thus, tan x = \(\frac{4}{3}\), sin x = -\(\frac{4}{5}\), cosec x = -\(\frac{5}{4}\)
cos x = -\(\frac{3}{5}\) and sec x = - \(\frac{5}{3}\)

Question 4.
sec x = \(\frac{13}{5}\), x lies in fourth quadrant.
Answer:

Question 5.
tan x = -\(\frac{5}{12}\), x lies in second quadrant.
Answer:

Question 6.
Find the value of sin 765°.
Answer:
We know that values of sin repeats after an interval or 2π
Thus, sin(765°) = sin(720° + 45°)
= sin (2 × 360° + 45°) = sin 450
(∵ After repeat it will come in first quadrant)
= \(\frac{1}{\sqrt{2}}\) Thus sin 765° = \(\frac{1}{\sqrt{2}}\)

Question 7.
Find the values of cosec(- 1410°)
Answer:
We know that values of cosec x repeats after an interval or 2π.
Thus, sec(-1410°) = cosec(-1410° + 4 × 360°)
= cosec (-1410° + 1440°)
= cosec 30°
(After repat this angle will shift to first quadrant)
= 2
Thus, cosec(-1410°) = 2
(Note : 4 × 360° is’taken since its approximate value is 1410°)

Question 8.
Find the value of tan 19 it
Answer:
We know that the values of tan x repeats after an interval of π. Therefore
tan \(\frac{19 \pi}{3}\) = tan(\(\frac{\pi}{3}\) + 6π) = tan(3 × 2π + \(\frac{\pi}{3}\))
= tan \(\frac{\pi}{3}\)
(After repeat this angle will shift to first quadrant and all trigonometric ratios are positive in first quadrant)
= √3
Thus tan \(\frac{19 \pi}{3}\) = √3

Question 9.
Find the value of sin\(\left(-\frac{11 \pi}{3}\right)\)
Answer:
We know that the values of sin x repeats after an interval of 2π.

Question 10.
Find the value of cot\(\left(-\frac{15 \pi}{4}\right)\)
Answer: