RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 Relations and Functions Miscellaneous Exercise

Question 1.
The relation f is defined by

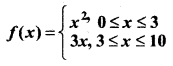
The relation g is defined by

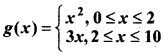
Show that f is a function and g is not a function.
Answer:
(i) Relation f is defined by

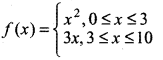
Domain of this relation = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} or {x: x, 0 ≤ x ≤ 10}
Now, f(0) = 0, f(1) = 1,
f(2) = 4,
f(3) = 9,
f(4) = 12,
f(5) = 15,
f(6) = 18,
f(7) = 21,
f(8) = 24,
f(9) = 27,
f(10) = 30
Now, Co-domain of relation = {0, 1, 4, 9, 12, 15, 18, 21, 24, 27, 30}
We see that each element of domain of relation f has a unique image in co-domain. This f is a function.

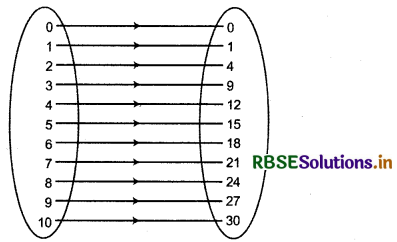
Second Method: If we make ordered pair of domain and co-domain of relation then we get {(0, 0), (1,1), (2, 4), (3, 9), (4,12), (5,15), (6,18), (7, 21) (8, 24), (9, 27),(10, 30)}.
We see that first element of these ordered pairs are distinct. Thus, f will be function.

(ii) Again, For relation g

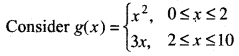
Domain of relation g = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

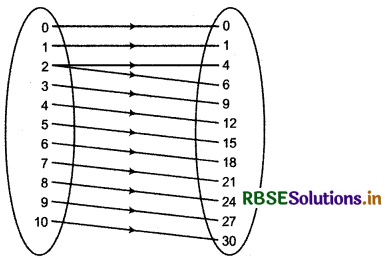
Now, from g(x) = x²
g(0) = 0, g(1) = 1, g(2) = 4
and from g(x) = 3x
g( 2) = 6, g(3) = 9, g(4) = 12, g(10) = 30
Here, we see that in domain of relation of element 2 have two images 4 and 6. So, relation is not a function.

Question 2.
If f(x) = x², find \(\frac{f(1.1)-f(1)}{(1.1-1)}\).
Answer:
∵ f(x) = x²
then f(1.1) = (1.1)² = 1.21
f(1) = 1² = 1
Thus, \(\frac{f(1.1)-f(1)}{(1.1-1)}=\frac{1.21-1}{0.1}=\frac{0.21}{0.10}\)
= 2.1
∴ Required value = 2.1

Question 3.
Find the domain of the function
f(x) = \(\frac{x^2+2 x+1}{x^2-8 x+12}\).
Answer:
f(x) = \(\frac{x^2+2 x+1}{x^2-8 x+12}\)
Here x² - 8x + 12 = (x - 6) (x - 2)
If x = 6 or x = 2, then function f(x) is not defined at x = 6 and 2. Thus, domain of f will be set of all real number except x = 6, x = 2 i.e. domain of function will be R-{2, 6}.
or Domain = (x: x ∈ R and 2, 6 ∉ R}
Since function will not be defined forx = 2 and x = 6.
⇒ Domain = R - {2, 6}

Question 4.
Find the domain and the range of the real function f defined by f(x) = √(x - 1).
Answer:
f(x) =√(x - 1)
Here, f is real function and x ∈ R
If x is less than 1 function will not be real. Thus for x - 1 ≥ 0 or x ≥ 1 function is defined. Thus domain of function will be set of all real numbers equal to or greater then 1 i.e.
Domain = {x : x ∈ R, x ≥ 1}
∵ Domain = [1, ∞)
here value of functions x = 1 is 0.
Since, f(1) = √1 - 1 = 0
and for remaining values of x, value of f(x) will be real numbers greater then 0.
Thus, range of functions = {x : x ∈ R, x > 0}
or [0, ∞)

Question 5.
Find the domain and the range of the real function f defined by f(x) = |x - 1|.
Answer:
∵ f(x) = |x - 1| is real function and will be positive for each value of x.
Thus, domain of function = set of all real numbers set = R
or Domain of function = (- ∞, ∞)
Range of function will be set of all positive real numbers i.e. range of given function = {x: x ∈ R, x ≥ 0} or Range = [0, ∞)

Question 6.
Let f = \(\left\{\left(x, \frac{x^2}{1+x^2}\right): x \in \mathbf{R}\right\}\) be a function from R into R. Determine the range of f.
Answer:

and 1 - y > 0 ⇒ 1 > y .
Thus, to define function value of y should be greater than 0 but should be less than 1.
Thus, range = {x: x ∈ R, 0 ≤ x < 1}

Question 7.
Let f, g : R → R be defined, respectively by f(x) = x + 1, g(x) = 2x - 3. Find f + g, f - g and \(\frac{f}{g}\).
Answer:
f(x) = x + 1, g(x) = 2x - 3
then (f + g) (x) = f(x) + g(x)
= x + 1 + 2x - 3
Thus (f + g) (x) = 3x - 2
or (f + g) = 3x - 2
Now (f - g) (x) = f(x) - g(x)
= (x + 1) - (2x - 3)
= x + 1 2x + 3
= 4 - x
or (f - g) = 4 - x

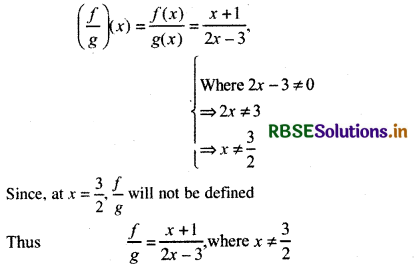
Question 8.
Let f = {(1 ,1), (2, 3), (0, -1), (-1, -3)} be a function from z to z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Answer:
f = {(1, 1), (2, 3), (0, -1), (-1, -3)} from Z to Z and f(x) = ax + b,
Now (1, 1), (0, - 1) ∈ f
Thus, f(1) = a × 1 + b = 1 → a + b = 1 ........... (1)
and f(0) = a × 0 + b = - 1
⇒ 0 + b = - 1
or b = - 1
then f(1) = a + b = 1 [From equation (1)]
or a - 1 = 1 Putting {b = - 1}
⇒ a = 1 + 1 ⇒ a = 2
Thus, a = 2, b = - 1
Required value a = 2, b = - 1

Question 9.
Let R be a relation from N to N defined by R = {(a, b): a, b ∈N and a = b²}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b)∈ R implies (b, a) ∈ R
(iii) (a, b) ∈ R (h, c) ∈ R implies (a, c) ∈ R
Justify your answer in each case.
Answer:
R = {(a, b): a, b ∈ N and a = b²}
(i) (a, a) ∈ R, is not true since except 1, no number equal to square of itself i.e. 1 = 12 but 2 ≠ 2², 3 ≠ 3² and 4 ≠ 4² etc.
(ii) (a, b) ∈ R implies (b, a) ∈ R is not true. It is not true. Since,
4 = 2² but 2 ≠ 4²
(a, b) ∈ R; (b, a) ∈ R is true when,
then (a, b) = (b, a)
Now, a = b²
Thus, (b², b) = (b, b²)
or b² = b
or b² - b = 0
or b(b - 1) = 0
or b = 0 or b = 1
Since, 0 ∉ N
[0 is not a natural number]
Thus, if a = 1, then statement is true but not true for other natural numbers.
Thus, statement is not true for all natural numbers.

(iii) (a, b) ∈ R and (b, c) ∈ R implies a = b² and b = c².
Then a = (c²)² = c⁴, √a = c². Thus, (a, c) ∈ R is not true.
Thus given statement is not true.

Question 10.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) f is a relation from A to B.
(ii) f is a function from A to B.
Justify your answer in each case.
Answer:
(i) A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16}
and f = {( 1,5), (2, 9), (3,1), (4,5),(2,11)}
Now,
A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3 ,1), (3, 5), (3, 9), (3, 11), (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
We see that all elements of relation of occurs in A × B f is relation from A to B. Since f ⊂ A × B.
f is a function from A to B this is not true. Since, first element of ordered pair (2, 9) and (2, 11) are repeated.

Question 11.
Let f be the subset of Z × Z defined by f = {(ab, a + b):a, b ∈ Z}. Is f a function from Z to Z? Justify your answer.
Answer:
Given f = {(ab, a + b): a, b ∈ Z)
if a = 3 and b = 4, then ab = 3 × 4 = 12
and a + 6 = 3 + 4 = 7
Thus (12, 7) ∈ f
Again a = 12, b = 1 then ab = 12 × 1 = 12
and a + b = 12 + 1 = 13
Thus (12, 13) ∈ f
We see that for of for element 12 of domain two images v and 13 are obtained. Thus relation from z to z is not a function.

Question 12.
Let A = {9, 10, 11, 12, 13} and let f:A → N, be defined by f(n) = the highest prime factor of n. Find the range of f.
Answer:
A = {9, 10, 11, 12, 13} and f: A → N. f(n) = n
f = {(n, f(n), n is highest prime factor of n
Now, 9 = 3 × 3, 10 = 2 × 5, 11 = 11 × 1,
12 = 2 × 2 × 3, 13 = 13 × 1
n = 9, f(9) = 3. n = 10, f(10) = 5
n = 11, f(11) = 11, n = 12, f(12) = 3,
n = 13, f(13) = 13
Since, highest prime factor for 9, 3, 5 for 10, 11 for 11, 3 for 12 and 13 for 13.
Thus, Range of f = {3, 5.11, 3, 13}
or Range = {3.5, 11, 13}