RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 Relations and Functions Ex 2.3

Question 1.
Which of the following relations are functions? Give reasons. If it is a function determine its domain and range.
(i) {{2,1) (5,1), (8,1), (11,1), (14,1), (17,1)}
(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14, 7)}
(iii) { (1,3), (1,5), (2 5)}
Answer:
(i) Given Relation
Let R = {(2, 1), (5, 1), (8,1), (11, 1), (14, 1), (17, 1)}
Here, Second element of each ordered pair is 1 which is unique. Thus, given relation is a function and this is constant function. Range of this constant function = {1}.

(ii) Given Relation
Let R = {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Here, each first element of ordered pair has unique image.
Thus, this relation is a function its Range.
Range = {1, 2, 3, 4, 5, 6, 7}

(iii) Given Relation
Let R = {(1, 3), (1, 5), (2, 5)} is not function, since first element of two ordered pairs are same eg. first element of (1, 3) and (1, 5).

Question 2.
Find the domain and range of the following real functions:
(i) f(x) = - 14
(ii) f(x) = \(\sqrt{9-x^2}\)
Answer:
Given function f(x) = -|x| is a real function
∴ x ∈ R, where R is set of real numbers. So, its domain is set of real numbers R set of real number R also represents as R (- ∞, ∞) is domain of given function.
Now, image of x is negative for all values of x since f(x) = -|x|
Thus, Range of given function will be zero and set of negative real numbers.
It is represented by (- ∞, ∞}
Thus, Range = (- ∞, 0] and Domain = (- ∞, ∞).
Note : 1. Set of real numbers is (- ∞, ∞) or R.
2. Set of positive real numbers (0, ∞) or R⁺
3. Set of negative real numbes (- ∞, 0) or R^-

(ii) Given function is a real function
f(x) = \(\sqrt{9 - x^2}\)
So, for all values of x, (9 - x²) is a real number.
It means, 9 - x² ≥ 0 or 9 ≥ x² or x² ≤ 9
i. e. - 3 ≤ x ≤ 3
Since, (- 3)² = 9 and (3)² = 9, (-2)² = 4, 2² = 4
Square of all the numbers between - 3 and 3 is < 9.
Thus, domain of function = {x: - 3 ≤ x ≤ 3 and x ∈ R}
For in range

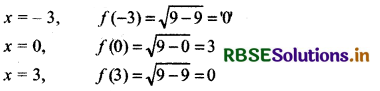
Thus, Range = {x: 0 ≤ x ≤ 3, x ∈ R}

Question 3.
A function f is defined by f(x) = 2x - 5, write down the values of:
(i) f(0),
(ii) f(7),
(iii) f(-3)
Answer:
(i) f(x) = 2x - 5
For x = 0,
f(0) = 2 × 0 - 5 = - 5
Thus, f(0) = - 5

(ii) f(x) = 2x - 5
For x = 7,
f(7) = 2 × 7 - 5
= 14 - 5 = 9

(iii) f(x) = 2x - 5
For x = -3,
f(-3) = 2 × (- 3) -5 = - 6 - 5 = - 11
Thus, f(-3) = - 11

Question 4.
The function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is 9C defined by t(C) = \(\frac{9 C}{5}\) + 32. Find:
(i) t(0)
(ii) t(28)
(iii) t(- 10)
(iv) The value of C. when t(C) = 212
Answer:
Since, function t maps temperature in degree Celsius into Fahrenheit such that
(i) t(C) = \(\frac{90}{5}\) + 32
For C = 0, t(0) = \(\frac{9 \times 0}{5}\) + 32
Thus, t(0) = 32

(ii) t(C) = \(\frac{9 C}{5}\) + 32
For C = 28, t(28) = \(\frac{9 \times 28}{5}\) + 32
= \(\frac{252}{5}\) + 32 = 50.4 + 32 = 82.4

(iii)

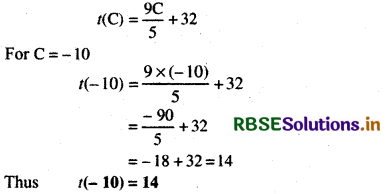
(iv) when t(C) = 212, then

Question 5.
Find the range of each of the following functions : (i) f(x) = 2 - 3x, x ∈ R, x > 0.
(ii) f(x) = x² + 2, x is a real number.
(iii) f(x) = x, x is a real number.
Answer:
f(x) = 2 - 3x, x ∈ R, x >0
Here, for x >0, f(x), may be negative or zero and its maximum value will be less than 2.
Let y - f(x) = 2 - 2x, x > 0
or y = 2 - 3x or 3x = 2 - y
or x = \(\frac{2-y}{3}\) ⇒ f(y) = \(\frac{2-y}{3}\)
If x > 0, then \(\frac{2-y}{3}\) >0
or 2 - y > 0
or 2 > y
or y < 2 ⇒ f(x) < 2
Thus, range of given function will be (-∞, 2)

(ii) f(x) = x² + 2
Since, x is a real number. So, x² will be positive real number. Thus, x² + 2 is also positive real number and for x = 0 its minimum value will be 2.
Thus, range of function will be [2, ∞).
This question can be solve in the following way also
Let y = f(x) = x² + 2
Where x is a real number
y = x² + 2
or x² = y - 2
or x = √y - 2
Now, x is a real number.
Thus, range of function will be [2, ∞)

(iii) f(x) = x, x is a real number.
Let y = f(x) = x or y = x
y will be real number for each x.
Since, y = x
Thus, large of function = set of real numbers = R
where R = (- ∞, ∞)
⇒ Range = (-∞, ∞)