RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 Relations and Functions Ex 2.2

Question 1.
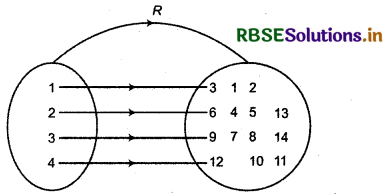
Let A = {1, 2, 3, .............. 14}. Define a relation R from A to A by R = {(x, y), 3x - y = 0, where x, y ∈ A}. Write down its domain, co-domain and range.
Answer:
Given
A{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} and R = {(x, y); 3x - y = 0 where x ∈ A and y ∈ A}
Now, solving 3x - y = 0, y = 3x
Then, R = {(1, 3), (2, 6), (3, 9), (4, 12)}
Domain of R will be {1, 2, 3, 4}
Range of R will be {3, 6, 9, 12}
Venn diagram

Co-domain
R = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} = A

Question 2.
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, xis a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
Answer:
We know that set of natural numbers is represented by N and relation R on set N is as follows :
R = {(x, y), y = x + 5, x is a natural number less than 4 and x, y ∈ N]
Here, In ordered pair (x, y), x is less than 4.
Thus, x = 1, 2, 3 and y = 5 more than x
Thus, y = 6, 7, 8 since y = x + 5
If x = 1, y = 1 + 5 = 6 ,
x = 2, y = 2 + 5 = 7
x = 3, y = 3 + 5 = 8

Venn diagram:

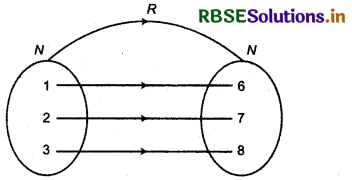
Thus, relation will be R = {(1,6), (2,7), (3,8)}.
Domain of relation R {1, 2, 3} and range will be {6, 7, 8}.

Question 3.
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y)} the difference between x and y is odd; x ∈ A, y ∈ B). Write R in roster form.
Answer:
Here A = {1, 2, 3, 5} and B = {4, 6, 9). Relation R from A to B is such that
R = {(x, y): The difference between x and y is odd x ∈ A, y ∈ B}
Now A × B = {(1, 4), (1, 6), (1, 9), (2,4), (2, 6). (2, 9), (3, 4), (3, 6), (3, 9), (5, 4), (5, 6), (5, 9)}
We know that difference of two even number is a even number and difference of two odd number is also a even number. Thus R will contain such pair contains will one even number and other odd number so their difference will be a odd numbers.
Thus, R = {(1. 4), (1, 6), (2, 9), (3,4), (3, 6), (5, 4), (5, 6)}

Question 4.
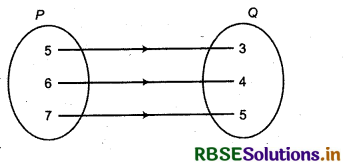
The figure shows a relationship between the sets P and Q. Write this relation
(i) In set-builder form
(ii) Roster form
What is its domain and range?

Answer:
R be the relation between sets P and Q such that R = {(5, 3), (6, 4), (7, 5)}, where P = {5, 6, 7} and Q = {3, 4, 5}.
From figure, it is clear that y = x - 2 where x ∈ P and y ∈ Q, since if x = 5. then y - 5 - 2 = 3 ∈ Q, then in builder form R can be written as:
(i) R = {(x, y): y = x - 2, for x = 5, 6,7
(ii) In Roster form R = {(5, 3), (6, 4), (7, 5)}
Domain of relation R will be, {5, 6,7} and range will be {3, 4, 5}.

Question 5.
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b); a, b ∈ A, b is exactly divisible by a}.
(i) Write R is Roster form,
(ii) Find the domain of R,
(iii) Find the range of R.
Answer:
Here A = {1, 2, 3, 4, 6} and ‘Relation R on A is such that R = {(a, b):a, b ∈ A] b is exactly divisible by a.
Now A × A = {(1, 1), (1, 2), (1, 3) (1,4), (1,6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 6),(3, 1), (3, 2), (3, 3), (3, 4), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 6)}
We will take those elements of A × A in which each ordered pair first element divides second element exactly. Thus,
(i) R = {(1,1), (1, 2), (1, 3),(1, 4), (1,6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii) Range of R = {1, 2, 3, 4, 6}

Question 6.
Determine the domain and range of the relation R defined by R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4,5}}.
Answer:
Given: Relation R = {(x, x + 5):
x ∈ {0, 1, 2, 3, 4, 5}}
x = 0 → x + 5 = 0 + 5 = 5
x = 1 → x + 5 = 1 + 5 = 6
x = 2 → x + 5 = 2 + 5 = 7
x = 3 → x + 5 = 3 + 5 = 8
x = 4 → x + 5 = 4 + 5 = 9
x = 5 → 5 = 5 + 5 = 10
Now, writing R in Roster form :
R = {(0,-5), (1, 6), (2,7), (3,8), (4, 9), (5,10)}
then Domain of R = {0, 1, 2, 3, 4, 5} and Range of R = {5, 6,7,8,9,10}

Question 7.
Write the Relation R = {(x, x³): x, x is a prime number less than 10} in Roster form.
Answer:
Relation R = {(x, x³): x is a prime number less than 10}
We know that prime number less than 10 are 2, 3, 5, 7.
Thus, Roster form of R will be as follows :
R = {(2, 2³), (3, 3³), (5, 5³), (7, 7³)}
or R = {(2, 8), (3, 27), (5, 125), (7, 343)}

Question 8.
Let A = {x, y, 4 and B = {1, 2}. Find the number of relations from A to B.
Answer:
Here, A = {x, y, z} contains 3 elements and B = {1, 2} contains 2 element i.e. n (A) = 3, n (B) = 2
Now, numbers of elements in A × B will be 6, Since,
n (A × B) = n(A) × n(B) = 3 × 2 = 6
Total subsets of A × B = 2⁶ = 64.
Thus, number of total relations from A to B = 2⁶ = 64

Question 9.
Let R be the relation on Z defined by R = {(a, b):a, b ∈ Z, a - b is an integer. Find the domain and range of R.
Answer:
Here Relation R on Z
R = {(a, b): a, b ∈ Z, a - b is an integer
We know that Z is set of integer and difference to two integers is also an integer.
Thus, a ∈ Z and b ∈ Z, then a - b ∈ Z, since a - b is also an integer.
Then, relation from Z to Z.
R = (a, b): a ∈ Z b ∈ z, a - b ∈ Z}
Thus, Domain of R = Z and Range of R = Z
Set of integers Z an domain and range of relation R respectively.